Putting Distance Between Collider Events
Using statistical tests to make sense of large datasets is an integral part of modern science and especially of collider physics. Model selection—selecting which candidate model provides a good explanation of a set of data—is an important case. For example, one might want to test whether the kinematics of particles produced in high-energy collisions imply the presence of a hypothetical particle. A related example is the classification of events. When two high-energy protons collide, they produce a huge number of subatomic particles with various energies and momenta. How can researchers, given measurements of these quantities, decide what type of collider event they are witnessing? Are they observing just a set of typical quantum chromodynamic (QCD) hadronic jets, or might the collision products contain top quarks or Higgs bosons? Patrick Komiske, of the Massachusetts Institute of Technology and Harvard University, and co-workers have proposed a “metric” that provides a new way to quantify how “distant” two collider events are [1]. As the authors show, this metric can be used to develop a relatively simple and easy-to-use classification tool that is nearly as effective as state-of-the-art machine-learning techniques requiring significantly more computational effort.
Driven by the peculiarities of the problems they face, researchers have developed a wide palette of clever test statistics. Chi-squared and likelihood-ratio tests, which measure how well competing models fit a given a set of data, are well known examples. Astronomers sometimes use the mean integrated squared error (MISE), similar to chi-squared. MISE measures the overlap between two probability density functions (PDFs). It is well suited for comparing similar PDFs, but when the two functions are well separated, MISE produces tiny numbers: it would be difficult to determine whether, for instance, two Gaussian PDFs were separated by 10 standard deviations or 20 because the two functions have essentially zero overlap. MISE is not well suited as the basis of a classification tool for high-energy collider events, since even similar events could have weakly overlapping PDFs.
The “earth mover’s distance” (EMD) [2], based on the so-called Wasserstein metric [3, 4], is an interesting alternative to MISE. It can be described as the minimum amount of energy needed to move a given “pile of earth” (that is, the first function) so that it turns into another pile (the second function). The EMD depends on the amount of earth that flows from the first pile to the second and on how far it flows. The EMD depends linearly on separation rather than exponentially, as MISE does, so the difference between 10 and 20 standard deviations is just a factor of 2. In other words, EMD emphasizes separation, rather than overlap (Fig. 1).
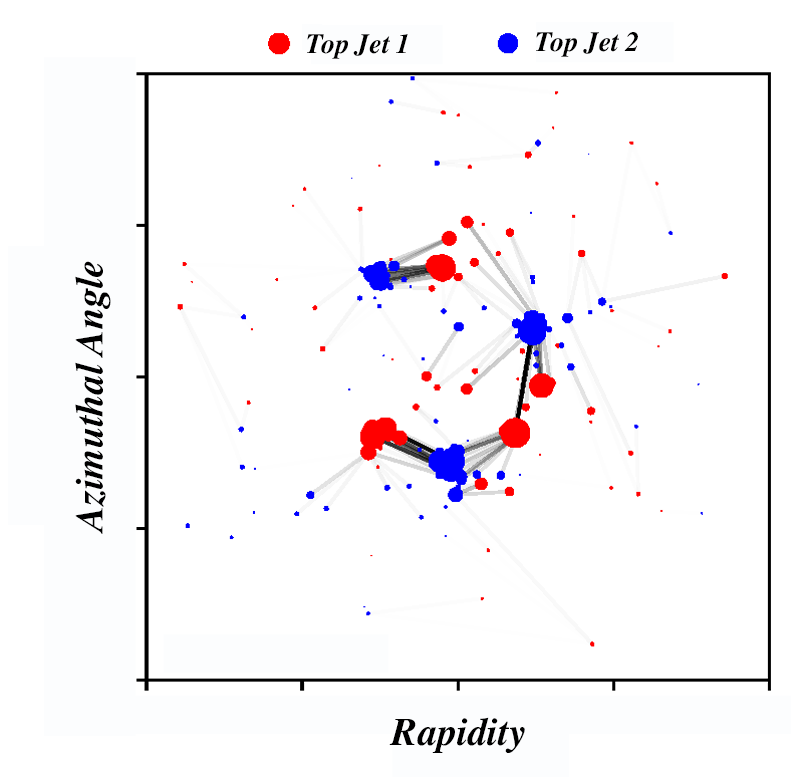
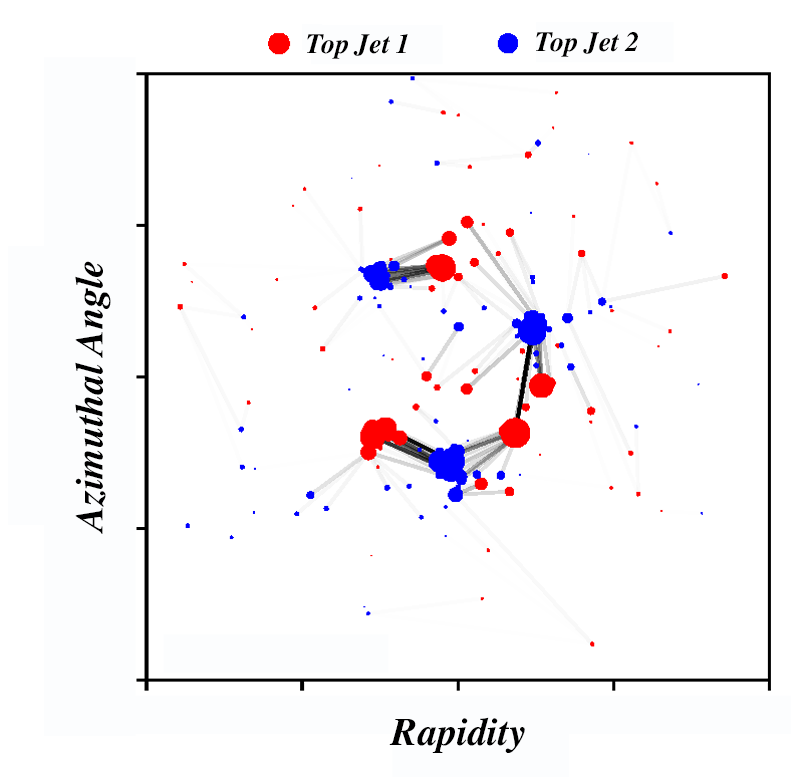
Can the EMD be used to quantify the difference between two collider events, for example between one involving the production of two top quarks and another associated with just a bunch of hadronic jets? Classifying events requires comparing their features. One approach is to define an abstract mathematical space whose dimensions correspond to different features of an event. Using a Monte Carlo event generator, one can simulate events, tagging each one as containing top quarks or just jets. Then, a real collision event is located in this space, based on its features, and the tags of the nearby simulated events are examined. If they are mainly top quark events, then the real collision event is probably a top quark event too. The success of this nearest-neighbor classification scheme depends critically on how the metric measuring the distance between events is defined. The choice of metric is not obvious—how does one compare quantitatively a difference in momentum with a difference in polar angles, given that they have different units?
Komiske and his colleagues suggest using the EMD as this distance metric [1]. In their example, they aim to distinguish hadronic W boson decays, such as those found in top quark events, from ordinary QCD jets. The authors compute the EMD by taking the particles in the W boson jet and transporting them to match the particles in the QCD jet. Calculating this distance requires a smart algorithm, but once the distance has been calculated, the nearest-neighbor algorithm is easy to apply, without any “training” or extensive optimization process. One simply evaluates the fraction of nearest neighbors that are tagged as W jets and classifies the real event accordingly. This simplicity stands in stark contrast to highly sophisticated deep learning techniques that take the particle momenta as direct inputs or that represent an event as an “image,” where one “pixel” corresponds to one calorimeter detector element. Komiske and his co-workers show that a simple EMD-based nearest-neighbor classifier performs nearly as well as advanced deep learning techniques.
This paper introduces additional, exciting ideas. A collision event has structure at many levels and scales. First, there is the configuration of jets in the event, and second, there is the arrangement of particles inside a given jet. While jets and the particles within them are randomly distributed, they are not simply isotropic, and their nonuniform kinematic distributions contain interesting physics. Since the authors’ EMD is based on the individual particles in an event, one can expect that the EMD encodes information about such distributions. If so, can one use the EMD to distinguish, on a statistical basis, three subjets produced in the decay of a top quark decay from a single large jet, for example?
Komiske and his co-workers address this question by introducing a mathematical quantity called the correlation dimension [5, 6]. This quantity relates physical effects that determine the event’s detailed structure to the scales of the event (e.g., energy or momentum). It turns out that the EMD captures structural details in a remarkable way. For instance, the authors show that top quark events have a richer structure than QCD multijet events at certain energy scales (on the order of the mass of the W boson), even when the gross features of the events are the same. As a second application of the correlation dimension, the authors study hadronic jets with the same energy but with a wide range of jet masses and show that the jets with high mass have a more elaborate internal structure than jets with low mass. This new approach may enable new studies of QCD and insights into jet formation—currently topics of great interest at the Large Hadron Collider.
It will be interesting to see where the ideas and techniques presented in this short and thought-provoking paper will bring us. The new EMD-based metric may well lead to better event classification techniques that enable experimenters to discover new physics beyond the standard model. In addition, the application of the correlation dimension to their new metric might bring new insights into standard model physics, such as the formation and structure of hadronic jets.
This research is published in Physical Review Letters.
References
- P. T. Komiske, E. M. Metodiev, and J. Thaler, “Metric space of collider events,” Phys. Rev. Lett. 123, 041801 (2019).
- O. Pele and B. Taskar, “The tangent earth mover’s distance,” in Geometric Science of Information - First International Conference, Paris, France, August 2013, Proceedings, edited by F. Nielson and F. Barbaresco (Springer, Berlin, 2013), p. 397[Amazon][WorldCat].
- L. N. Wasserstein, “Markov processes over denumerable products of spaces describing large systems of automata,” Problems Inform. Transmission 5, 47 (1969).
- R. L. Dobrushin, “Prescribing a system of random variables by conditional distributions,” Theor. Probab. Appl. 15, 458 (1970).
- P. Grassberger and I. Procaccia, “Characterization of strange attractors,” Phys. Rev. Lett. 50, 346 (1983).
- B. Kégl, “Intrinsic dimension estimation using packing numbers,” in Advances in Neural Information Processing Systems 15, Proceedings of the 2002 Neural Information Processing Systems Conference, Vancouver, Canada, edited by S. Becker, S. Thrun, and K. Obermayer (MIT Press, Cambridge, 2003), p. 681[Amazon][WorldCat].