Spin Polarization Without Net Magnetization

Aurélien Manchon; Jakub Železný

Viewpoint

Spin Polarization Without Net Magnetization

¹Interdisciplinary Nanoscience Center of Marseille (CINaM), Aix-Marseille University, Marseille, France
²Institute of Physics, Academy of Sciences of the Czech Republic (ASCR), Prague, Czech Republic

July 15, 2020• Physics 13, 112

An analysis of magnetic symmetry groups in antiferromagnets points to a new class of materials that will be useful for spintronics.

Figure caption — **Figure 1:** Crystal and magnetic structure of ${MnF}_{2}$ showing two electron trajectories (green arrows). As ${MnF}_{2}$ is a collinear antiferromagnet, the spin directions (thick red arrows) of the Mn atoms (blue spheres) share a common axis. Electrons traveling along the crystal axis interact equally with spin-up and spin-down Mn atoms. Electrons traveling at an angle to the crystal axis interact more with spin-up Mn atoms than with spin-down ones. Energy degeneracy is therefore lifted between bands of opposite spins along specific momentum directions.

Great soccer players know how to impart spin to the ball so that it swerves past the goalkeeper. In an analogous way, researchers can play with the interconnected spin and momentum of a material’s electrons to engineer new physical effects [1]. In the simplest ferromagnets, for example, spins aligned along or against the material’s magnetic moment lie in different energy bands. This band “splitting” promotes the spin polarization of flowing electrons—an effect that lies at the core of spintronics. In certain nonmagnetic materials, on the other hand, electrons passing through at a specific angle are spin polarized in one direction preferentially, producing a spin-splitting effect despite the absence of magnetism. A vast literature has attributed the origin of this momentum-dependent spin orientation to spin-orbit coupling (SOC), a relativistic effect connecting the spin and orbital degrees of freedom at the atomic scale [2]. Lin-Ding Yuan and colleagues now show that a similar effect can be obtained in the absence of SOC, by taking advantage of a material’s antiferromagnetic order instead [3]. Other groups have proposed this idea [4]. But the new work from Yuan and co-workers is based on an analysis of magnetic space groups, which paves the way to the identification of a new class of materials with spin-polarizing properties.

In crystals with SOC, electrons’ spins align along the spin-orbit-induced magnetic field, and their orientations therefore depend on the direction of their linear momentum. This dependence, or “spin texture,” produces exotic phenomena such as the spin Hall effect—the creation of a pure spin current transverse to the direction of the injected current flow [5]. If the crystal structure also lacks inversion symmetry, flowing electrons can create a transient magnetization whose orientation depends on the direction of injection [2]. However, generating a sufficiently large SOC to create a spin texture requires heavy elements, and materials incorporating these elements are often fragile and sometimes toxic. Generating spin textures without relying on SOC is a big deal for spintronics because it eliminates the need to deal with such “complicated” materials.

A first clue to how this can be done was offered about sixty years ago by Soloman Pekar and Emmanuel Rashba [6]. They suggested that a spatially inhomogeneous magnet could host spin-flip excitations driven by an external electric field. These flips occur because, in inhomogeneous fields, electrons’ spins are intertwined with their position in the lattice, producing a spin texture in momentum space. Driving an electron from one point in the magnet to another would therefore compel its spin to flip. Building on this idea, Yuan and colleagues suggest that localized magnetic fields in an antiferromagnet could do a similar job.

Antiferromagnets have magnetic order at the atomic scale but no overall magnetic moment. Nevertheless, recent studies of these materials have revealed a range of spin-related phenomena such as spin polarization [4] and the magnetic spin Hall effect [7, 8] . These findings make antiferromagnets promising materials for spintronics [9], and they suggest that a spin texture is indeed present even in the absence of SOC [8].

In their study, Yuan and colleagues report the emergence of momentum-dependent spin splitting, rather than a spin texture [3]. In particular, they focus on the spin splitting arising from a simple collinear antiferromagnetic order in the absence of SOC. This distinction is important, as the two phenomena yield materials with differing properties. When spin texture arises from SOC, the spin directions vary continuously across momentum space. But with spin splitting, the material’s collinear antiferromagnetic order imposes a common spin orientation. In spin splitting, therefore, the energy degeneracy is lifted between bands of opposite spins along specific momentum directions. Like the SOC-induced spin texture, such spin splitting supports spin polarization of flowing electrons along certain crystallographic directions, as well as a transverse spin current similar to the spin Hall effect [10]. Unlike the SOC-induced spin it cannot promote the current-driven magnetization.

The key issue that Yuan and colleagues address is the conditions under which the spin splitting occurs. Nonmagnetic crystals are classified by their space group, which combines point symmetries with lattice translations. Magnetic crystals, on the other hand, are classified by their magnetic space group, which contains in addition the time-reversal symmetry operator $𝜃$ . Yuan and colleagues explain that spin degeneracy is protected by preserving two pairs of symmetry operations: the combination of time-reversal symmetry $𝜃$ with inversion symmetry $I$ , and the combination of a spin rotation $U$ with a translation of the lattice $T$ . As a result, even centrosymmetric antiferromagnets (in which SOC-induced spin textures are inhibited) can display spin splitting when both $𝜃 I$ and $U I$ are broken. They find that this combination only happens in so-called type I and III magnetic space groups.

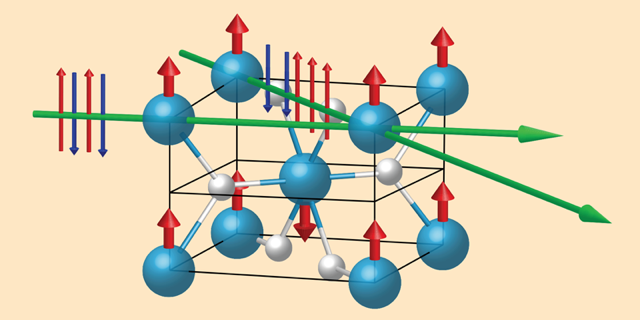
To illustrate this approach, the researchers demonstrate that ${MnF}_{2}$ , a well-known collinear antiferromagnet belonging to magnetic space group III, exhibits spin splitting only along certain directions in momentum space (Fig. 1). They show that the spins remain aligned along the direction of the antiferromagnetic order, and that the degeneracy is lifted between bands with opposite polarity. However, the most attractive aspect of this theory is not the existence of the momentum-dependent spin splitting—which is elegant but not unprecedented—but the methodology that they use to search for candidate antiferromagnets. Applied to large materials databases now available, their method could lead to the discovery of novel light antiferromagnets that promote spin-current generation and current-driven spin excitations.

A thrilling question with exciting implications is whether it’s possible to extend this analysis to the search for spin texture rather than spin splitting. It seems reasonable to speculate that certain light, noncentrosymmetric antiferromagnets (or other complex magnets) that lack SOC could host useful spin textures supporting current-driven magnetic excitations in a similar manner to ${Mn}_{2} Au$ or $CuMnAs$ [9]. In fact, this study echoes recent predictions of magnetic spin Hall effect in the absence of SOC made for noncollinear ${IrMn}_{3}$ and ${SnMn}_{3}$ [7], and collinear ${RuO}_{2}$ [10]. Another interesting aspect put forward by Yuan and colleagues is that the magnitude of the predicted spin splitting is much larger than spin-orbit-coupling-induced splitting. Finding a similar enhancement for spin textures could be of great interest to spintronics applications.

This research is published in Physical Review B.

Correction (14 September 2020): An earlier version of the article implied that Yuan and colleagues are the first to predict spin-splitting in an antiferromagnet. In fact, the phenomenon was predicted recently by several groups. The references and first paragraph were updated to provide this information.

References

J. W. M. Bush, “The aerodynamics of the beautiful game,” in Sports Physics, edited by C. Clanet (Les Editions de l’Ecole Polytechnique, Paris, 2013), p. 171[Amazon][WorldCat].
A. Manchon et al., “New perspectives for Rashba spin–orbit coupling,” Nat. Mater. 14, 871 (2015).
L.-D. Yuan et al., “Giant momentum-dependent spin splitting in centrosymmetric low-Z antiferromagnets,” Phys. Rev. B 102, 014422 (2020).
L. Šmejkal et al., “Crystal time-reversal symmetry breaking and spontaneous Hall effect in collinear antiferromagnets,” Sci. Adv. 6, eaaz8809 (2020); K.-H. Ahn et al., “ ${RuO}_{2}$ Antiferromagnetism in as d-wave Pomeranchuk instability,” Phys. Rev. B 99, 184432 (2019); S. Hayami, “Momentum-dependent spin splitting by collinear antiferromagnetic ordering,” J. Phys. Soc. Jpn. 88, 123702 (2019).
J. Sinova et al., “Spin Hall effects,” Rev. Mod. Phys. 87, 1213 (2015).
S. I. Pekar and E. I. Rashba, “Combined resonance in crystals in inhomogeneous magnetic fields,” Sov. Phys. JETP 20, 1295 (1965), [J. Exp. Theor. Phys. 47, 1927 (1964)].
Y. Zhang et al., “Spin Hall effect emerging from a noncollinear magnetic lattice without spin–orbit coupling,” New J. Phys. 20, 073028 (2018).
J. Železný et al., “Spin-polarized current in noncollinear antiferromagnets,” Phys. Rev. Lett. 119, 187204 (2017).
T. Jungwirth et al., “The multiple directions of antiferromagnetic spintronics,” Nat. Phys. 14, 200 (2018).
R. González-Hernández et al., “Magnetic spin Hall effect in collinear antiferromagnets,” arXiv:2002.07073.

About the Authors

Aurélien Manchon received his Ph.D. from Joseph Fourier University, France, in 2007. After that, he was a postdoctoral fellow at the University of Missouri and then at the University of Arizona. In 2009, he joined the King Abdullah University of Science and Technology (KAUST, Saudi Arabia) as faculty, where he conducted theoretical research on spintronics. His research interest spans from spin-orbit-coupled transport to chiral magnetism, antiferromagnets, ultrafast spin dynamics, and two-dimensional materials. He has recently moved back to France as a Professor of Physics in the Centre Interdisplinaire de Nanoscience de Marseille (CINaM) at Aix-Marseille University. He enjoys exploring novel mechanisms at the nanoscale, collaborating with experimentalists, and hiking the Calanques with his four kids.

Jakub Železný is a group leader at the Institute of Physics of the Czech Academy of Sciences in Prague. He works on theoretical condensed-matter physics, primarily in the field of spintronics. His research mainly focuses on spintronics in antiferromagnetic and other unconventional magnetic materials and on the role that symmetry plays in transport phenomena. He received his Ph.D. from Charles University in the Czech Republic in 2016, and after that he was a postdoctoral fellow at the Max Planck Institute for Chemical Physics of Solids in Germany.