Ticking Toward a Nuclear Clock

Lars von der Wense

Viewpoint

Ticking Toward a Nuclear Clock

JILA, University of Colorado Boulder, Boulder, CO, USA

September 28, 2020• Physics 13, 152

The high-precision measurement of a nuclear transition of a thorium isotope is a key step towards the development of a nuclear optical clock.

Figure caption — **Figure 1:** Artist’s rendition of a nuclear optical clock.

Today’s most accurate clocks tick at frequencies defined by ultranarrow electronic transitions of atoms at optical wavelengths. These optical atomic clocks are accurate to within one part in $1 0^{18}$ , meaning that they’d slip by less than one second over the age of the Universe. However, an even more accurate clock could, in principle, be built by using a nuclear transition instead of an electronic transition. Since the atomic nucleus is much smaller than the atomic electron shell, such a “nuclear optical clock” (Fig. 1) is expected to be less sensitive to external perturbations.

Long ago, researchers identified a nuclear transition suitable for a nuclear clock in the thorium-229 isotope. However, until recently, the transition frequency was not determined with sufficient precision to allow its direct excitation with narrow-band lasers—a prerequisite for the operation of an optical clock. Tomas Sikorsky of Heidelberg University, Germany, and colleagues have now reported a high-precision measurement of the thorium-229 transition that significantly narrows the spectral range on which future searches should focus [1]. The results pave the way for even more precise measurements based on laser spectroscopy. Knowledge of the exact transition frequency would immediately make a nuclear optical clock possible.

Since the laser was invented in 1960, laser spectroscopy of the electronic shells of atoms has become an established technique and has enabled spectacular applications, including optical atomic clocks. Conversely, laser spectroscopy of a nuclear transition remains elusive. The reason is simple: Transitions involving nuclear excited states have typical energies in the keV to MeV range, which is inaccessible by today’s laser technology.

A transition of the thorium-229 nucleus is the only known exception. The energy difference between its ground state and its first, metastable excited state, denoted $^{229 m} Th$ , is exceptionally low—with previously reported values between 3.5 and 8.3 eV [2–7]. These energies correspond to wavelengths where lasers are, in principle, available. However, since the transition frequency wasn’t known with sufficient precision, it wasn’t clear which laser technology would be most appropriate. And finding the precise frequency with a narrow-band laser would have required prohibitively long scans and multiple types of lasers.

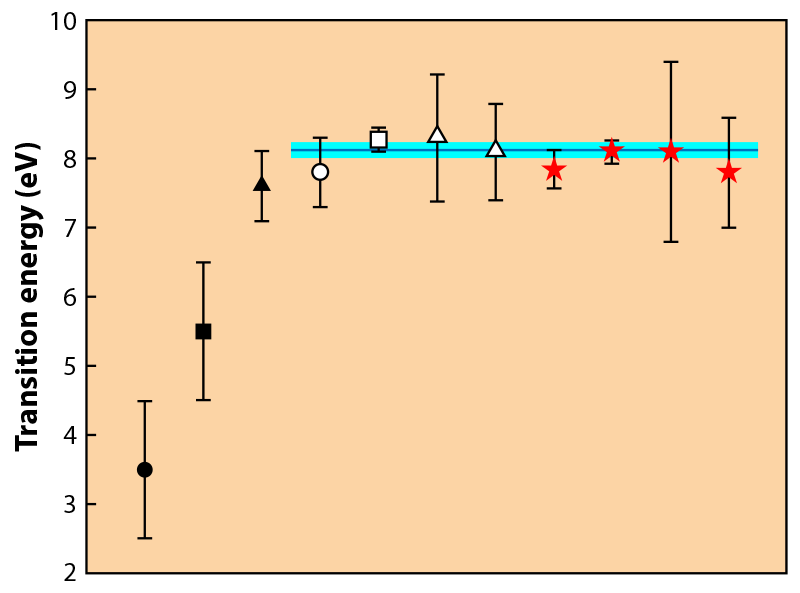
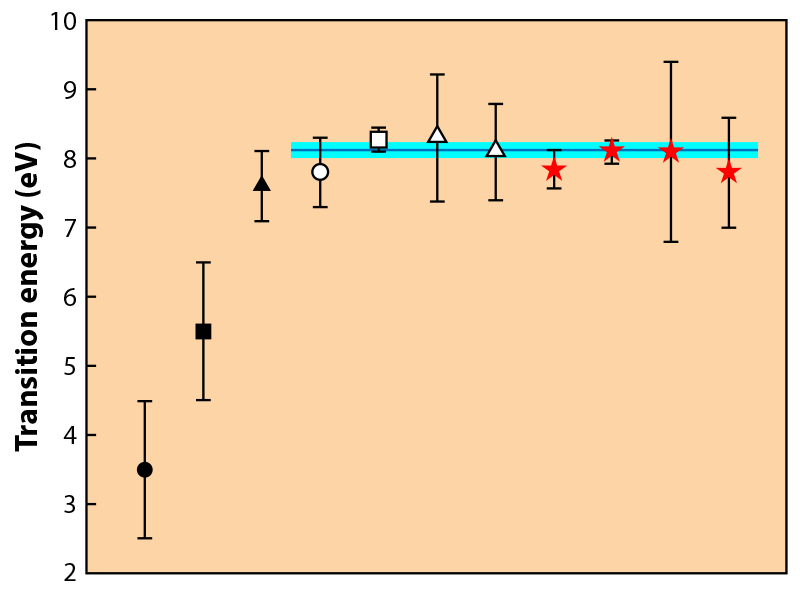
The precise determination of the $^{229 m} Th$ energy remained an elusive experimental objective for decades. With high-precision laser spectroscopy ruled out, such searches relied on observables that are indirectly related to the transition frequency. Studies based on the measurement of gamma rays emitted in a nuclear decay involving $^{229 m} Th$ initially estimated the transition at about 3.5 eV [2]. More precise values derived from gamma-ray emission have led to a significant shift of the measured transition energy to around 7.6 eV in 2007 [4] and to 7.8 eV in 2009 [5]. In 2019, three additional values were obtained using different techniques, all pointing to a slightly higher central value for the transition energy [6, 7].

Sikorsky and his colleagues from several institutes in Heidelberg, Vienna, Mainz, and Darmstadt, have now provided four additional values—derived through slightly different procedures— for the transition energy. Figure 2 compares these new values to all the energy values that have been published since 1994. Although the experiments rely on vastly different techniques, the plot shows a converging trend: The eight most recently obtained values are in reasonable agreement, with an uncertainty-weighted mean energy value of $8.12 \pm 0.11$ eV. The new values dramatically boost the confidence that we are getting closer to pinpointing the isomer’s energy.

To obtain $^{229} Th$ in its metastable state, Sikorsky and colleagues use an established technique based on the alpha decay of uranium-233. This decay produces various states of the $^{229} Th$ nuclei, including $^{229 m} Th$ , and is accompanied by the emission of multiple gamma-ray lines. Each of these lines corresponds to a transition between specific nuclear levels of $^{229} Th$ . The $^{229 m} Th$ energy can then be inferred by subtracting the measured energies of appropriate gamma-ray lines.

This approach is the same as that used in some of the earlier studies [4, 5], but the new measurements make a leap in the accuracy, thanks to better resolution of the gamma-ray detection. For their experiments, Sikorsky and co-workers developed a gamma spectrometer based on magnetic microcalorimeters—highly sensitive detectors in which the temperature increase caused by the absorption of a photon is converted into a magnetization decrease. This spectrometer featured a full-width-half-maximum (FWHM) resolution of less than 10 eV at a gamma-ray energy of 30 keV—the highest resolution ever obtained at this energy and 3 times better than that of the spectrometer employed in Refs. [4] and [5]. Importantly, by carefully measuring the shape of each gamma-ray line, the line’s center can be determined to higher precision than the FWHM resolution.

Factoring in the spectral resolution and all possible sources of error, the authors derive an overall uncertainty for the most precise of their four values (8.10 eV) of only 0.17 eV—on par with the previous best value, $8.28 \pm 0.17$ eV [6]. The new determination has an important advantage, though. The researchers’ analysis shows that the reported value is limited by statistical, rather than systematic uncertainty. Hence, by running the same experiment over longer times, their approach has the potential to further reduce the uncertainty.

The new results offer important guidance for the direct study of $^{229 m} Th$ through laser spectroscopy. The narrowed spectral range for the transition will shorten the time required for a laser-based scan, and it already determines what laser technology would be most suitable for precision spectroscopy: Since no continuous wave lasers exist at around 8.1-eV energies, today’s only option is offered by frequency combs—laser sources with spectra consisting of equidistant lines that enable exceptionally precise spectroscopic measurements. An experiment along these lines is currently being conducted [8].

Once researchers are able to excite the nuclear transition directly with lasers, a nuclear optical clock could be immediately developed. Such a clock, first proposed in 2003 [9], offers the potential for a tenfold accuracy improvement compared with the best atomic clocks in operation today [10]. An important application would be the test of potential time variations of the fine structure constant $𝛼$ . A recent study showed that the frequency of a thorium clock would be an ultrasensitive probe of such variations, which could allow researchers to improve existing constraints by about 6 orders of magnitude [11].

References

T. Sikorsky et al., “Measurement of the ²²⁹Th isomer energy with a magnetic microcalorimeter,” Phys. Rev. Lett. 125, 142503 (2020).
R. G. Helmer and C.W. Reich, “An excited state of ²²⁹Th at 3.5 eV,” Phys. Rev. C 49, 1845 (1994).
Z. O. Guimarães-Filho, “Energy of the 3/2⁺ state of ²²⁹Th reexamined,” Phys. Rev. C 71, 044303 (2005).
B. R. Beck et al., “Energy splitting of the ground-state doublet in the nucleus ²²⁹Th,” Phys. Rev. Lett. 98, 142501 (2007).
B. R. Beck et al., “Improved value for the energy splitting of the ground-state doublet in the nucleus Th,” Lawrence Livermore National Laboratory Report No. LLNL-PROC-415170 (2009).
B. Seiferle et al., “Energy of the ²²⁹Th nuclear clock transition,” Nature 573, 243 (2019).
A. Yamaguchi et al., “Energy of the ²²⁹Th nuclear clock isomer determined by absolute $𝛾$ -ray energy difference,” Phys. Rev. Lett. 123, 222501 (2019).
L. von der Wense, and C. Zhang, “Concepts for direct frequency-comb spectroscopy of ^229mTh and an internal-conversion-based solid-state nuclear clock,” Euro. Phys. J. D 74, 146 (2020).
E. Peik and C. Tamm, “Nuclear laser spectroscopy of the 3.5 eV transition in ²²⁹Th,” Europhys. Lett. 61, 181 (2003).
C. J. Campbell et al., “Single-ion nuclear clock for metrology at the 19th decimal place,” Phys. Rev. Lett. 108, 120802 (2012).
P. Fadeev et al., “Sensitivity of ²²⁹Th nuclear clock transition to variation of the fine-structure constant,” arXiv:2007.00408.

About the Author

Lars von der Wense is working as a Humboldt Fellow at JILA, University of Colorado Boulder. After studying physics and mathematics at the University of Hamburg, Germany, and the University of Cambridge, UK, he received his Ph.D. in 2016 from Ludwig Maximilian University (LMU) of Munich for his work on the direct detection of ^229mTh. Since then he has continued his ^229mTh-related research as a postdoctoral fellow at LMU and at JILA, where he is preparing an experiment devoted to the ^229mTh laser excitation. For his work on ^229mTh, he received the Röntgenpreis of the University of Giessen and the Theodor-Hänsch-Preis of LMU Munich.

Measurement of the ${}^{229}{Th}$ Isomer Energy with a Magnetic Microcalorimeter

Tomas Sikorsky, Jeschua Geist, Daniel Hengstler, Sebastian Kempf, Loredana Gastaldo, Christian Enss, Christoph Mokry, Jörg Runke, Christoph E. Düllmann, Peter Wobrauschek, Kjeld Beeks, Veronika Rosecker, Johannes H. Sterba, Georgy Kazakov, Thorsten Schumm, and Andreas Fleischmann

Phys. Rev. Lett. 125, 142503 (2020)

Published September 28, 2020

Read PDF