Verifying Weak Turbulence Theory
Wave phenomena are ubiquitous at all scales throughout the Universe, and where there are waves, there’s the potential for wave turbulence. Wave turbulence is the physical state that arises in a continuous medium when a large number of wave modes interact with each other randomly. This state is present in many interesting physical applications, the list of which continues to grow [1]. To mention just a couple of recent examples: gravitational-wave turbulence could have played an important role in the very first moments of the Universe [2], while wave turbulence involving dark-matter fields has been proposed as a driver of galaxy formation [3]. A specific case of wave turbulence in which weakly nonlinear waves propagate in an unbounded space is described by weak turbulence theory (WTT). Capturing the dynamics of this regime will be helpful to accurately model large fluid systems, such as the oceans and atmosphere, but because the necessary wave properties are difficult to reproduce in the laboratory, the theory has gone largely untested. Now, Eduardo Monsalve and colleagues, of the French National Center for Scientific Research (CNRS) and the University of Paris-Saclay, report a unique experiment in which the challenge has been successfully addressed for wave turbulence in a rotating fluid, thereby achieving one of the rare clean confirmations of WTT [4].
WTT starts with a nonlinear partial differential equation describing waves in a particular physical system. Then, by assuming that the waves have small amplitudes, random phases, and a broadband spectrum, it derives a wave kinetic equation for that system’s wave spectrum. The theory’s central finding is the Kolmogorov–Zakharov (KZ) spectrum—a power-law stationary solution of the wave kinetic equation describing the way energy is apportioned across waves of different frequencies. This solution is a direct analog of the famous Kolmogorov spectrum of hydrodynamic turbulence, which corresponds to the energy cascade from large to small scales of motion. The KZ spectrum was first discovered by Vladimir Zakharov for a simplified wave model [5]; later, spectra were predicted for a vast number of physical wave systems. For inertial waves in rotating fluids—the system studied by the Paris-Saclay group—the KZ spectrum was calculated by Sébastien Galtier [6].
A long-standing goal of lab experiments has been to confirm that real wave systems follow the KZ spectrum. The fact that previous attempts have generally achieved only limited success is due to the difficulties in creating wavefields that are not affected by the finite size of the experiment (and the resulting discreteness of the wave modes) or by the presence of strongly nonlinear coherent structures, such as solitons, the sharp crests of breaking waves, or persistent vortices. For example, researchers studying wave turbulence on a water surface were unable to observe the KZ spectrum even in a rather large wave tank [7, 8]. In addition, experiments on rotating turbulence have consistently reported deviations from the Galtier spectrum.
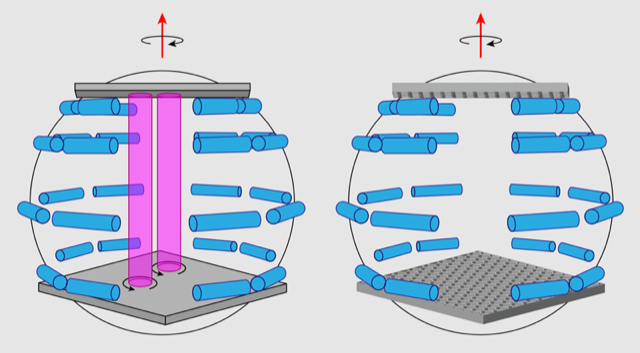
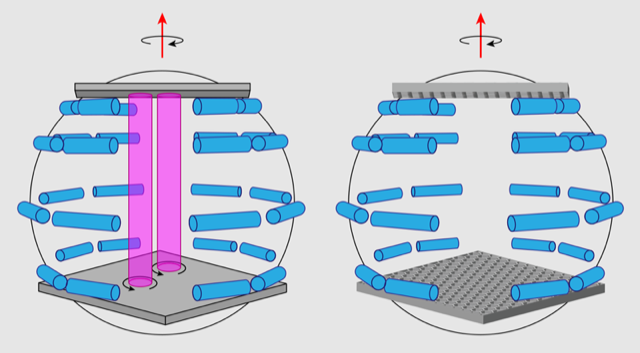
Overcoming these challenges is the culmination of an effort reported by the Paris-Saclay team over several publications. Their previous study identified the major reason why inertial waves in a rotating fluid deviated from the WTT predictions [9]. The reason was a rapid generation of geostrophic modes—columnar vortices that are uniform along the wave tank’s rotation axis. The 2D rotation of these geostrophic modes is strongly nonlinear, breaking a key assumption of WTT. Moreover, when they are sufficiently strong, these modes can modify the dynamics of the 3D inertial waves propagating through the fluid. They also reported an effective method of suppressing the geostrophic motion with little impact on wave dynamics by introducing a horizontal honeycomb grid into the water tank. This finding was instrumental in understanding which further modifications should be made to achieve a state with weak inertial-wave turbulence—the project that they have now successfully implemented.
In their latest experiment, Monsalve and colleagues have built on their earlier setup by adding a second horizontal honeycomb grid to their apparatus (Fig. 1), allowing them to fully suppress the geostrophic modes [4]. The second crucial modification was an upgrade of the wave-driving mechanism, which enabled a threefold increase in the maximum vibration amplitude. This capability allowed them to avoid wave interactions being dominated by resonances between discrete wave modes—a usual consequence of the finite size effect [10]. Roughly, the waves collide with each other over distances much smaller than the distance between the walls; therefore, their dynamics are insensitive to the presence of the boundaries. In this improved experiment, the researchers observed a gradual discrete-to-continuous transition in the mode interactions when the vibration amplitude was increased. For strong vibrations, they succeeded in measuring a power-law spectrum with exponent close to −5∕2, thereby confirming the Galtier spectrum predicted by WTT.
Monsalve and co-workers’ recent work contains two messages that may help researchers create wave turbulence in other systems. First, some wave systems have a tendency to generate “slow manifolds”—nonwave motions that can severely affect the wave dynamics and should be suppressed in experiments aiming to observe wave turbulence. In rotating inertial waves, these slow manifolds are geostrophic flows. But, as the researchers explain, the manifolds can take the form of layered flows in stratified fluids or zonal jets in large-scale atmospheric Rossby waves. The second message is that great care should be taken with the wave-generation mechanism to avoid a big influence from finite-size effects. Following these two guidelines, researchers will be in a better position to study the role of wave-turbulent states in the atmosphere or ocean. They might also be able to use WTT to improve the small-scale inputs to climate models and weather predictions.
References
- S. Nazarenko, “Wave turbulence,” Contemp. Phys 56, 359 (2015).
- S. Galtier and S. V. Nazarenko, “Turbulence of Weak Gravitational Waves in the Early Universe,” Phys. Rev. Lett. 119, 221101 (2017).
- J. Skipp et al., “Wave turbulence in self-gravitating Bose gases and nonlocal nonlinear optics,” Phys. Rev. A 102, 043318 (2020).
- E. Monsalve et al., “Quantitative experimental observation of weak inertial-wave turbulence,” Phys. Rev. Lett. 125, 254502 (2020).
- V. E. Zakharov, “Weak turbulence in media with a decay spectrum,” J. Appl. Mech. Tech. Phys. 4, 22 (1965).
- S. Galtier, “Weak inertial-wave turbulence theory,” Phys. Rev. E 68, 015301 (2003).
- P. Denissenko et al., “Gravity wave turbulence in a laboratory flume,” Phys. Rev. Lett. 99, 014501 (2007).
- S. Lukaschuk et al., “Gravity wave turbulence in wave tanks: Space and time statistics,” Phys. Rev. Lett. 103, 044501 (2009).
- M. Brunet et al., “Shortcut to geostrophy in wave-driven rotating turbulence: The quartetic instability,” Phys. Rev. Lett. 124, 124501 (2020).
- V. S. L’vov and S. Nazarenko, “Discrete and mesoscopic regimes of finite-size wave turbulence,” Phys. Rev. E 82, 056322 (2010).