Deadlocked Order and Disorder in the Strongest Metals
Metals researchers have known for decades that there exists in polycrystalline metals a “strongest” crystallite size, or grain size: For grains of around 10 to 20 nm, a peak appears in the metal’s strength, and any change in the average grain size leads to a weakening of the material [1]. On the more-studied “near side” of this peak, the material softens as the grains get larger because defects in the grains, known as dislocations, have more room and therefore can be moved more easily. There is a well-known scaling law that captures this softening trend, and also numerous models for it. The metal also softens on the “far side” of the peak as grain size shrinks, but for mysterious reasons that need further elaboration. Now Michael Chandross and Nicolas Argibay, both at Sandia National Laboratories in New Mexico, present a simple physical scaling law that captures the far-side weakening trend in metals [2]. The roots of their law lie in the physics of disordered amorphous structures.
The study of how grain size affects a metal’s strength has a long history. In the early 1950s, researchers established a scaling law—the Hall-Petch law—connecting the two quantities. That law quickly became part of the central canon of materials science [3, 4] and predicts that polycrystalline metals get stronger as the size of their grains is reduced. It provided a roadmap for the structural metals industries for decades, encouraging them to develop techniques to produce metals with ever smaller grains, which today can be m or less.
But the Hall-Petch law is now known to break down for metals made of nanometer-sized grains [5, 6]. For metals with grains of this size, the boundary region between the grains becomes increasingly important. The boundaries are much more disordered than the insides of the crystal grains, and that disorder influences the metal’s behavior. As the grain size tends to zero, materials scientists expect the properties of polycrystalline metals to converge to those of a chemically equivalent amorphous solid [5]. Since amorphous (glassy) forms of a material are softer than their polycrystalline equivalents, researchers have suggested that there must also be a “strongest grain size” on the nanoscale. Chandross and Argibay build on this idea to obtain a scaling law for the strength of nanocrystalline metals in the regime where the Hall-Petch law breaks down [2].
In developing their model, the researchers assume that the energy required to fully disorder a grain boundary is equal to that required to melt it. They then take that energy as the activation barrier for a grain boundary to start sliding. Examining the limit where mechanical loading provides all of that energy and where deformation occurs only in the grain boundaries, they derive an equation that predicts the strength of a metal in terms of its melting point, heat of fusion, and the volume fraction of the grain boundaries in the system. Their expression predicts that the strength of a nanocrystalline metal increases with increasing grain size because there are fewer grain boundaries to deform. This trend halts when the grain size crosses the curve of the Hall-Petch law, and deformation is instead dominated by dislocations within the grains. That crossover defines the peak strength achievable for a polycrystalline metal and represents a condition where the boundaries between the grains and the grains themselves have the same strength—the grains and their boundaries are deadlocked.
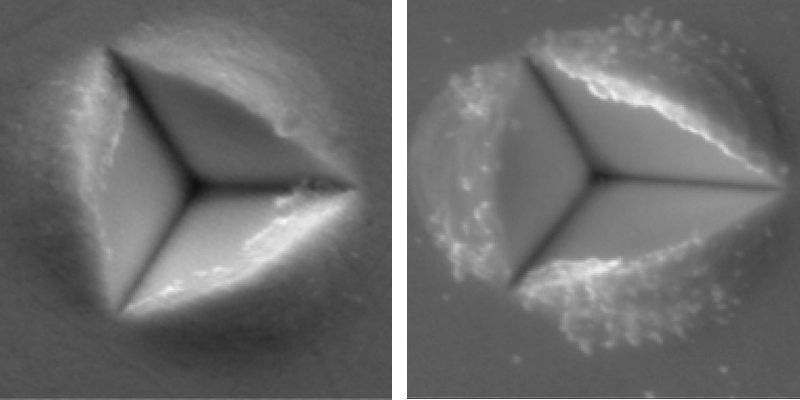
To support their model, Chandross and Argibay compare their predictions to available experimental data, for example that of nickel tungsten alloys [7]. In that alloy system the crossover in behavior from crystal-like to amorphous-like deformation is directly visible in experiments (Fig. 1). For large 20-nm grains, plasticity mostly occurs within the grains, leading to smooth and homogeneous deformation of the material. In contrast, for smaller -nm grains, plasticity occurs at the grain boundaries. In this case, grains get rearranged by sliding among each other, and the deformed material develops a lumpy surface as individual grains poke out. Somewhere in the middle, near a grain size of 10–12 nm, the crystals and the grain boundaries have equal strength, leading to the deadlock that gives the strongest grain size. The model of Chandross and Argibay predicts that this peak strength occurs for a grain size of about 10 nm, in agreement with experiments. What is more, their model captures the crossover without any new fitting parameters on the far side of the peak.
The scaling law of Chandross and Argibay is a welcome new model to understand the strength of metals, especially on the far side of the Hall-Petch peak, where we have few theories. Since its roots lie in an equivalence between mechanical yield and thermal disordering in an amorphous-like grain boundary, it will be interesting to see if connections can be made with glasses, where researchers seek a similar equivalence between the mechanical jamming-unjamming transition and the glass transition [8]. As scientists become more adept at stabilizing the size of nanocrystalline grains in metals, it will also be interesting to more quantitatively compare experiments with the new model [9].
Finally, another interesting experimental connection for the new model lies in its tacit prediction that a more disordered grain boundary should yield more easily. Such behavior has been reported in some nanocrystalline alloys [10], and it has inspired researchers to intentionally design different grain boundary “complexions” that contain controlled amounts of disorder [11]. The model’s use of simple physical input parameters should allow rapid screening of the strength and optimum grain sizes for different metals and metal alloys without the need for elaborate experiments or atomistic simulations. There are many devices that require components made of extremely strong metals, such as those found in mechanical equipment or electronics. These results could thus foreshadow a new generation of super-high-strength metals and metal alloys that capitalize on the deadlock between amorphous and crystalline deformation physics.
This research is published in Physical Review Letters.
References
- A. S. Argon and S. Yip, “The strongest size,” Philos. Mag. Lett. 86, 713 (2006).
- M. Chandross and N. Argibay, “Ultimate strength of metals,” Phys. Rev. Lett. 124, 125501 (2020).
- E. O. Hall, “The deformation and ageing of mild steel: III Discussion of results,” Proc. Phys. Soc. Sect. B. 64, 747 (1951).
- N. J. Petch, “The cleavage strength of polycrystals,” J. Iron Steel Inst. 173, 25 (1953).
- T. G. Nieh and J. Wadsworth, “Hall-Petch relation in nanocrystalline solids,” Scr. Metall. Mater. 25, 955 (1991).
- J. Schiøtz, “Atomic-scale modeling of plastic deformation of nanocrystalline copper,” Scr. Mater. 51, 837 (2004).
- J. R. Trelewicz and C. A. Schuh, “The Hall–Petch breakdown in nanocrystalline metals: A crossover to glass-like deformation,” Acta Mater. 55, 5948 (2007).
- A. J. Liu and S. R. Nagel, “The jamming transition and the marginally jammed solid,” Annu. Rev. Condens. Matter Phys. 1, 347 (2010).
- A. R. Kalidindi and C. A. Schuh, “Stability criteria for nanocrystalline alloys,” Acta Mater. 132, 128 (2017).
- T. J. Rupert et al., “Grain boundary relaxation strengthening of nanocrystalline Ni–W alloys,” J. Mater. Res. 27, 1285 (2012).
- J. D. Schuler and T. J. Rupert, “Materials selection rules for amorphous complexion formation in binary metallic alloys,” Acta Mater. 140, 196 (2017).