Blowin’ in the Wind Same as Flowing in H2O

Nathalie Vriend; Karol Bacik

Viewpoint

Blowin’ in the Wind Same as Flowing in H₂O

¹BP Institute for Multiphase Flow, University of Cambridge, Cambridge, UK
²Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Cambridge, UK

April 20, 2020• Physics 13, 62

A new model unifies the descriptions of sand transport by wind and water, a result that could lead to a better understanding of the movements of sediments on the surfaces of planets.

Figure caption — **Figure 1:** Sketch of a granular bed mobilized by fluid flow. In water (left), grains move by rolling and sliding in a narrow layer above the immobile bed, while in air (right), grains dance and hop along ballistic trajectories. A model from Pähtz and Durán hypothesizes that, despite phenomenological differences, the sediment transport rate follows the same scaling laws in both media. In both fluids, they find a critical level (dotted line), which divides the bed into two energetically distinct layers. Grains above this level are energized by the flow and dissipate energy though particle-particle collisions. Grains below this level barely move, but they absorb and dissipate the energy from grain-bed collisions.

Large swaths of Earth’s surface are covered in loose sediment. The grains that make up this sediment form fascinating bedforms from meandering riverbeds to wavy dunes [1, 2], whose shapes are constantly changing as water or air currents move the grains. The modeling of sediment transport has significantly advanced in recent years, but researchers lack a unifying framework to describe the transport of grains by different density fluids, like air and water. Now, a new model from Thomas Pähtz at Zhejiang University in China and Orencio Durán at Texas A&M University, College Station, makes an important step toward that unification [3]. The model could help in better understanding the transport of loose grains by different fluids, such as water or hydrocarbon fluids, in industrial processes and in environmental ones that shape the surfaces of Earth and other planets.

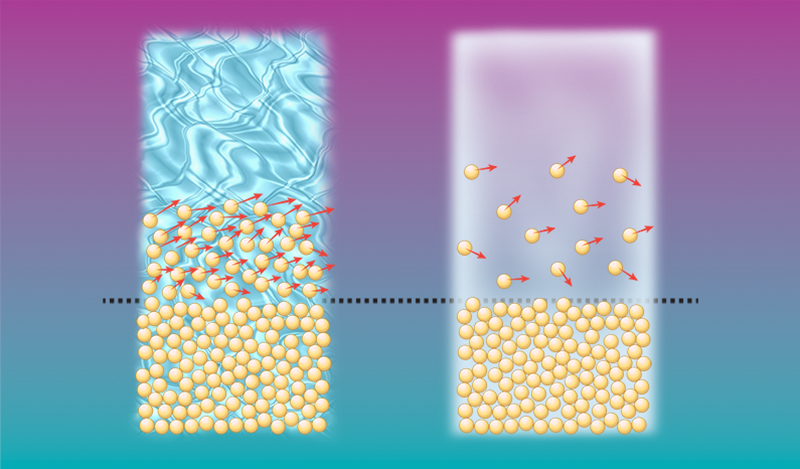
Consider a flat layer of sand over which wind or water flows. When the fluid flows gently (slowly and uniformly), the grains either quiver in place or don’t move at all. However, once the flow passes a threshold forcing, the fluid can propel grains and drag them downstream. This threshold determines whether a sandstorm erodes a dune or whether a river erodes its banks. The amount by which the forcing exceeds the threshold determines the quantity of sediment that is transported: a more vigorous current carries more sand.

Physically, these observations indicate a tight relationship between the rate of sediment transport $Q$ , the threshold fluid stress $𝜏_{0}$ , and the actual fluid stress $𝜏$ . If $𝜏$ lies below $𝜏_{0}$ , then $Q = 0$ and grains should stay stationary. For $𝜏$ exceeding $𝜏_{0}$ , drag overcomes the resistive forces and the grains migrate. Extensive experiments have been carried out to find exactly how the $Q$ of grains varies in air and water. For studies in wind tunnels, the results indicate that $Q$ scales linearly with the excess shear stress, $𝜏 - 𝜏_{0}$ [4, 5]. In contrast, studies in water flumes find a nonlinear relationship [6].

The traditional way of modeling sediment transport dates back to Ralph Bagnold, a British soldier and geologist, whose studies of sand were inspired by his desert explorations in North Africa [7]. His model and subsequent models of others are based on phenomenological arguments to explain the observed behavior for $Q$ . These arguments incorporate the different modes of transport for grains by wind and water [1]. In air, grains move by bouncing and hopping along the surface, a process known as saltation. In water, which is about 1000 times denser than air, saltation is damped, and grains move instead by rolling and sliding, a process called bedload. The study by Pähtz and Durán suggests that, as far as $Q$ is concerned, differentiating the transport this way is unnecessary, and they posit that $Q$ in fact obeys the same laws in both air and water [3].

In their model, Pähtz and Durán shift the focus from grain kinematics to energy balance, demonstrating that $Q$ is tightly linked to a type of energy dissipation. Using discrete element simulations, they calculate the contact forces between individual grains and quantify the energy dissipation that occurs in grain-grain collisions. Their simulations resolve each individual sand grain, providing a level of detail that experimentalists can only aspire to. As expected they find differences in the scaling of energy dissipation for the energetic grains bouncing near the surface and for their neighbors that remain almost still on the bed. Surprisingly though, they find the same energy-dissipation laws for different fluid environments.

Given this finding, why then are different scaling laws for $Q$ observed for wind and water systems? Pähtz and Durán, find a simple answer to the conundrum: the scaling is nonlinear, but the wind is too weak to reach that nonlinearity. They show that when $𝜏$ is sufficiently close to $𝜏_{0}$ , $Q$ can be approximated by a linear function, recovering the experimentally observed scaling of wind transport of grains as an asymptotic limit of their more general formula.

This new work is part of a broader project of Pähtz and Durán that blows fresh air on classical problems in sediment transport [3, 8, 9]. Their body of work introduces an elegant energy-dissipation framework for analyzing particle motion in sediment transport, and it displays remarkable agreement with experiments. But questions still remain about sand transport in different fluids, leaving open the quest for models that can be robustly deployed. Sediment transport, literally, lies at the interface of two very active research areas: granular mechanics and fluid turbulence. Pähtz and Durán focus on the behavior of the granular phase, but there are still many open questions regarding the overlying fluid flow and its interaction with the grains. For example, what role is played by turbulent vortices and turbulence-induced intermittency (which form the fluctuating components of the overlying flow) [10]? On the more applied end, it would be useful to explore what happens when we move away from ideal spheres toward more realistically shaped granular materials. Do the results of Pähtz and Durán still hold? Are there straightforward methods to include features such as packing disorder, polydispersity, or angularity of grains in sediment transport models? Fortunately for scientists, this research field is not yet out of breath.

References

B. Andreotti et al., Granular media: Between fluid and solid (Cambridge University Press, Cambridge, 2013)[Amazon][WorldCat].
F. Charru et al., “Sand ripples and dunes,” Annu. Rev. Fluid Mech. 45, 469 (2013).
T. Pähtz and O. Durán, “Unification of aeolian and fluvial sediment transport rate from granular physics,” Phys. Rev. Lett. 124, 168001 (2020).
O. Durán et al., “On aeolian transport: Grain-scale interactions, dynamical mechanisms and scaling laws,” Aeolian Res. 3, 243 (2011).
J. F. Kok et al., “The physics of wind-blown sand and dust,” Rep. Prog. Phys. 75, 106901 (2012).
E. Lajeunesse et al., “Bed load transport in turbulent flow at the grain scale: Experiments and modeling,” J. Geophys. Res. 115, F04001 (2010).
R. A. Bagnold, The physics of blown sand and desert dunes (Dover Publications Inc., Mineola, 2012)[Amazon][WorldCat].
T. Pähtz and O. Durán, “Fluid forces or impacts: What governs the entrainment of soil particles in sediment transport mediated by a Newtonian fluid?” Phys. Rev. Fluids 2, 074303 (2017).
T. Pähtz and O. Durán, “Universal friction law at granular solid-gas transition explains scaling of sediment transport load with excess fluid shear stress,” Phys. Rev. Fluids 3, 104302 (2018).
K. A. Bacik et al., “Wake induced long range repulsion of aqueous dunes,” Phys. Rev. Lett. 124, 054501 (2020).

About the Authors

Nathalie Vriend is a Royal Society University Research Fellow in the BP Institute at the University of Cambridge, UK. Her research program aims to gain a deeper understanding of the physics of dynamic granular materials using detailed laboratory experiments, targeted field work, numerical simulations, and theoretical modeling. Vriend leads a research group with active projects in granular rheology and avalanching, dune structure and migration, and sound propagation. In the past she worked on the dynamics of real snow avalanches, singing sand dunes, and seismic wave propagation.

Karol Bacik is a Ph.D. student in the Department of Applied Mathematics and Theoretical Physics at the University of Cambridge, UK. He obtained his B.Sc. degree from Imperial College London, UK, and a MASt in mathematics from the University of Cambridge. His academic interests include fluid mechanics and granular materials. Currently, he studies the dynamics of sand dunes using laboratory measurements and theoretical modeling.