Defect or No Defect: It’s a Toss Up
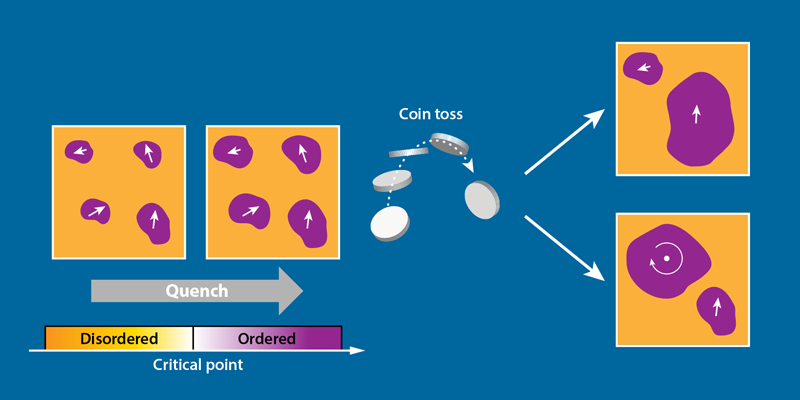
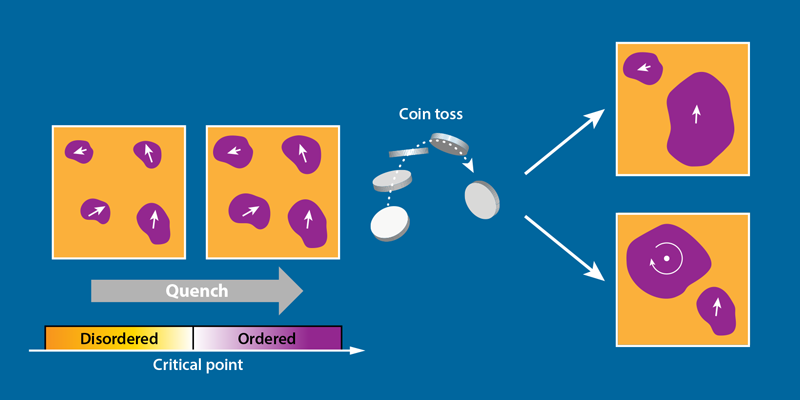
From nanoscale magnets to the cosmos itself, the onset of order is often accompanied by the development of defects having universal features. These topological defects form when the system is thrown out of equilibrium as it cools, or “quenches,” from a disordered phase into an ordered phase, inducing local pockets of order to grow and come together. A crowning theoretical prediction—developed over three decades ago by Tom Kibble [1] and Wojciech Zurek [2]—is that the density of topological defects obeys universal power-law scaling with respect to the quench rate. Now, Fernando Gómez-Ruiz from the Donostia International Physics Center in Spain and colleagues model the quenching process in terms of the probability that a defect forms at the juncture of multiple pockets. With this statistical picture, the researchers demonstrate that not only the mean defect density but also the entire defect distribution exhibits universal power-law scaling [3]. These findings are significant for exploring nonequilibrium phenomena in a range of systems including ultracold atoms, magnets, liquid crystals, and the early Universe.
Kibble’s original treatment envisioned that a phase transition in the early Universe led to a network of line defects, called “cosmic strings,” giving rise to structure formation. Zurek subsequently proposed that a similar mechanism could be at work in the very different context of tangles of vortex lines created in liquid helium-4. Both scenarios assume that the system is characterized by an order parameter, which, in its simplest form, points along a direction that can change from point to point. At high temperature, this order parameter has no preferred direction (disordered phase), but at low temperature, global alignment appears (ordered phase). As the system approaches the critical point that separates the disordered and ordered phases, the length scale over which the order is correlated grows larger and larger. Specifically, this length scale diverges as a universal power law with respect to a temperature variable that characterizes how close the system is to criticality. The timescale over which the system relaxes to equilibrium also exhibits universal power-law divergence.
So how do these defects form? As the cooling or quenching process begins, small regions of local order appear within the disordered medium. These regions form a mosaic of causally disconnected domains of local order, each pointing in a random direction with respect to the rest. The regions grow until they encounter each other. At a juncture of three or more domains, the orientation of the order parameter may form a circular pattern that is incongruent with a single direction. As a result, the juncture “winds” into a topological defect—a vortex in this case (Fig. 1). Most of the topological defects accrue close to the critical point when the relaxation of the system is too slow to keep up with the quench rate, thrusting the system out of equilibrium. Similar to the correlation length and relaxation time, the density of defects adopts a universal power-law scaling with respect to the quench rate, whereby faster quenching results in more defects.
The Kibble-Zurek scenario plays out in a range of systems, which can host a menagerie of topological beasts: kinks, domain walls, vortex loops, monopoles, hedgehogs, skyrmions, and more. Which of these defects forms depends on the dimensions of the system and on the topology of the order parameter. Beyond average defect density, the scenario relates to a slew of observables, including excitation densities, entropy, and residual energies. And it extends equally well to quenching across classical and quantum phase transitions, as has been explored in the paradigmatic case of the transverse-field Ising model for magnetism [4]. The Kibble-Zurek signatures can be difficult to observe, but several experiments over the past few decades have confirmed the predicted scaling in condensates, multiferroics, superconductors [5], and even laboratory settings mimicking cosmic strings [6].
The ingenuity of Gómez-Ruiz and co-workers’ approach [3] lies in framing the Kibble-Zurek picture as one in which a topological defect may nucleate at the junction of ordered domains. Or it may not. These two possibilities are like the flip of a biased coin, with the “nucleate” option having a specific probability p, and the “no nucleate” option having a probability 1−p. This probabilistic description allows analysis of the full counting statistics for the distribution of defects. As with any two-possibility probabilistic event, the authors postulate a binomial distribution for the number of defects produced in a given number of trials. This form enables them to relate the variance—as well as other higher-order correlations and fluctuations—to the average number of defects. To confirm this result, the authors demonstrate that their predictions agree with numerical simulations of stochastic dynamics in a 1D chain model having kink defects. The remarkable conclusion is that the entire statistical distribution follows the same universal scaling with respect to the quench rate.
These findings bear plentiful insights on the progression toward order, including the presence of long tails in the defect distribution and the condition for adiabaticity to be maintained such that no defects are produced. The predictions provide researchers with a way to analyze systems in which the statistics are limited by a relatively modest number of trials. The approach should also be valuable in understanding errors and switching processes in quantum annealers and simulators. The work comes at a very timely moment, given the surge of interest in nonequilibrium phenomena that relate to many-body localization, thermalization, and critical dynamics. Almost everywhere we look, we can find drastic, out-of-equilibrium shifts—the current pandemic being a glaring example.
Many fields are now ripe for exploring nonequilibrium predictions, like those from Gómez-Ruiz et al. The excellent control and dynamic tunability in ultracold gases have already unlocked a veritable playground for Kibble-Zurek physics [7]. Topological quantum matter, in its absence of local order, offers ground-state degeneracies, fractional defects, and entanglement features as alternative measures of the dynamics [8]. And quench studies in solid-state magnets are poised to probe the Ising model [9]. As for the early Universe, new observational probes could offer thrilling insights into how small-scale fluctuations govern structure formation [10], potentially revealing clues about the cosmos’ plunge from disorder to order.
This research is published in Physical Review Letters.
References
- T. W. B. Kibble, “Topology of cosmic domains and strings,” J. Phys. A 9, 1387 (1976).
- W. H. Zurek, “Cosmological experiments in superfluid helium?” Nature 317, 505 (1985).
- F. J. Gómez-Ruiz et al., “Full counting statistics of topological defects after crossing a phase transition,” Phys. Rev. Lett. 124, 240602 (2020).
- J. Dziarmaga, “Dynamics of a quantum phase transition and relaxation to a steady state,” Adv. Phys. 59, 1063 (2010).
- A. del Campo and W. H. Zurek, “Universality of phase transition dynamics: Topological defects from symmetry breaking,” Int. J. Mod. Phys. A 29, 1430018 (2014).
- I. Chuang et al., “Cosmology in the laboratory: Defect dynamics in liquid crystals,” Science 251, 1336 (1991).
- Jérôme Beugnon and Nir Navon, “Exploring the Kibble–Zurek mechanism with homogeneous Bose gases,” J. Phys. B 50, 022002 (2017).
- G. Kells et al., “Topological blocking in quantum quench dynamics,” Phys. Rev. B 89, 235130 (2014); A. Chandran et al., “Kibble–Zurek scaling and string-net coarsening in topologically ordered systems,” J. Phys. Condens. Matter 25, 404214 (2013).
- D. M. Silevitch, “A ferromagnet in a continuously tunable random field,” Nature 448, 567 (2007).
- N. Musoke, “Lighting the dark: Evolution of the postinflationary universe,” Phys. Rev. Lett. 124, 061301 (2020).