Surface Tension Scars Soft Solids
In daily life, we are surrounded by soft materials. Most biological tissue comprises materials that are soft, meaning that they readily deform under typical mechanical stresses. Large deformations of soft solids lead to complex morphologies that arise when the free surface succumbs, accordion-like, to a compressive force. Under enough compressive strain, a free interface will bend into a crease, generating deep, folded valleys and, ultimately, regions of self-contacting surfaces. Creases formed via compression in biological tissues permeate nature and include the sulci of the brain and the folds of a bent elbow. Such creases often persist in the form of a permanent “scar” on the surface of the soft material. However, despite the ubiquity of such features, it is not clear why scars remain once the stress is relaxed. Nor is it clear why creases form at a particular location in a homogenous material that’s compressed uniformly. Michiel van Limbeek, of the Max Planck Institute for Dynamics and Self-Organization in Germany, and his colleagues [1] now find that soft materials subjected to repeated cycles of deformation develop scars from a folding-unfolding asymmetry due to liquid wetting (Fig. 1).
One possibility that has previously been proposed to explain the appearance and persistence of scars on soft solids is a mechanism seen in other systems, such as folded or crumpled paper [2, 3]. In those cases, permanent weakening or damage alters the material’s mechanical properties locally, leaving specific sites vulnerable to subsequent creasing. Alternatively, adhesion between the two sides of a fold might cause the surfaces in the crease to stick together, producing a configuration that remains even when the stress is removed. But neither plastic deformation nor adhesion can account for sensitivity to liquid-solid surface tension.
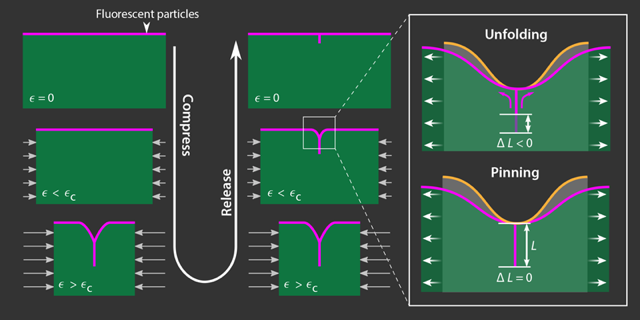
To understand the phenomenon of creases in soft materials, van Limbeek and his colleagues conducted an experiment involving a layer of soft polymer gel deposited on top of a pre-stretched rubber sheet. The soft polymer gel was then immersed in liquids with greater or lesser surface tension. By gradually relaxing the tension on the rubber sheet, they compressed the gel layer uniformly, one micrometer at a time. Eventually, the gel surface began to bend, ultimately forming a crease as the two sides of the bend came into contact with each other. Then the researchers released the compression gradually and observed how the surface uncreased—and how it didn’t—when the gel was immersed in different liquids.
Observations of the gel’s surface morphology with confocal microscopy allowed the researchers to measure directly the extent and angle of the gel’s deformation at the crease. Fluorescently labeled nanoparticles affixed to the gel’s surface highlighted the gel-liquid interface, making it possible to monitor the crease continuously as the two sides of the crease made contact and became otherwise inaccessible to direct measurement.
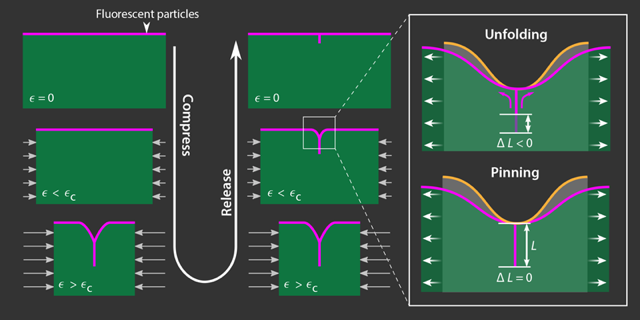
The experiments showed a hysteresis in the crease’s response to compression and relaxation. Specifically, the depth of the crease for a given strain depended on whether the gel was in the compression or relaxation phase of the cycle. Such a result would be expected if the system’s dynamics were controlled by adhesion between the two sides. However, adhesion alone cannot explain the way the surface profile changed while the full range of compression was applied and removed when the gel was immersed in different fluids. Under compression, the crease in cross section resembled the letter Y, with the Y’s “stalk” representing the self-contacting region and the “arms” representing the folded surface of the gel. When the compression was relaxed, the crease appeared more like the letter T, with the surface bending sharply into the area of self-contact (Fig. 2). The different shapes suggest that the unfolding process required more energy than was needed to form the crease in the first place when the surface tension increased. This energy difference could be accounted for by the need to overcome surface-tension forces in addition to adhesion between the two sides.
The researchers propose that the role of surface tension in this system parallels a phenomenon common in interfacial fluid mechanics known as contact-line pinning. When a liquid-air interface meets a solid surface—such as a liquid droplet resting on a tabletop—the three-phase junction forms what’s known as a contact line. The angle between the tabletop and the tangent to the liquid-air interface can be used to measure surface tension when the droplet is at equilibrium. When not at equilibrium, this stress drives the contact line to move; however, thanks to tiny surface heterogeneities, the contact-line motion is often not smooth. Experiments show that on the smallest scales, contact lines shift in fits and starts because they remain locally stuck or pinned in place [4]. Van Limbeek’s result shows that this same pinning of a contact line is responsible for the persistence of creases on soft solids.
As systems that exhibit strongly nonlinear behavior and large deformation, creases and interfacial folds have become useful tools for probing questions as mundane as “why does desiccated fruit wrinkle?” and as rich as “why does the brain have folds?” [5]. By identifying another nonlinear phenomenon that arises from contact-line pinning, van Limbeek and his colleagues have added to that investigative toolbox.
The discovery of an alternative mechanism for surface scarring in a similar (though not mechanically identical) way to how paper creases when repeatedly crumpled [6] could also have practical applications—for example, in soft-robotics devices that fold [7] or in surface engineering for fluid transport [8]. Indeed, one could envision manipulating the surface tension of soft solids to “program” their creasing pattern with a view to controlling the transport of liquids over such surfaces. Manipulating the local surface tension of a soft material that can expand by swelling might also offer a way to direct its morphological evolution, thus guiding a swelling surface to take on a desired shape [9]. By identifying the key role of contact-line pinning in the formation of such creases, van Limbeek and colleagues have opened the door for such applications.
References
- M. A. J. van Limbeek et al., “Pinning-induced folding-unfolding asymmetry in adhesive creases,” Phys. Rev. Lett. 127, 028001 (2021).
- T. Tallinen et al., “The effect of plasticity in crumpling of thin sheets,” Nat. Mater. 8, 25 (2008).
- O. Gottesman et al., “Furrows in the wake of propagating d-cones,” Nat. Commun. 6, 7232 (2015).
- D. M. Kaz et al., “Physical ageing of the contact line on colloidal particles at liquid interfaces,” Nat. Mater. 11, 138 (2011).
- E. Hohlfeld and L. Mahadevan, “Unfolding the sulcus,” Phys. Rev. Lett. 106, 105702 (2011).
- J. Andrejevic et al., “A model for the fragmentation kinetics of crumpled thin sheets,” Nat. Commun. 12, 1470 (2021).
- A. Firouzeh and J. Paik, “Robogami: A fully integrated low-profile robotic origami,” J. Mech. Robot. 7, 021009 (2015).
- M. Coux and J. M. Kolinski, “Surface textures suppress viscoelastic braking on soft substrates,” Proc. Natl. Acad. Sci. U.S.A. 117, 32285 (2020).
- Y. Klein et al., “Shaping of elastic sheets by prescription of non-Euclidean metrics,” Science 315, 1116 (2007).