Photons Get Slippery

Kaden Hazzard

Viewpoint

Photons Get Slippery

Department of Physics, Rice University, Houston, TX, USA

October 11, 2021• Physics 14, 139

Researchers have turned light into a superfluid by using a “synthetic” dimension, which is created by using temporal degrees of freedom to mimic spatial degrees of freedom.

Figure caption — **Figure 1:** Sketch of how an optical mesh lattice creates a synthetic dimension. (a) In real space, light moves from an initial point in space and time ( $x = 0, t = 0$ ) to reach different spatial coordinates ( $x$ ) at times ( $t = 1, 2, \dots$ ). (b) To realize a synthetic dimension, light pulses replicate this behavior in time, with time subintervals playing the role of effective spatial locations. (c) To realize the dynamics illustrated in (b), the researchers employ a scheme known as an optical mesh lattice, in which two fiber-optic loops of different sizes are connected by a beam splitter (open box).

Any physics student knows from their first lessons in optics that light moves in straight lines, unaffected by other light rays—beams from two flashlights do not bounce off each other. However, Martin Wimmer at the Friedrich Schiller University Jena, Germany, and colleagues have used a technique based on a so-called synthetic dimension to create pulses of light that interact and behave collectively as a superfluid [1]. In so doing, they have demonstrated this to be a tunable platform for exploring the interplay between many-body interactions, topology, and dissipation—features that are central to many fields of physics.

To understand the synthetic dimension, which is crucial to these experiments, note that a usual dimension of space is defined through a set of locations combined with a notion of “locality”: particles can interact with and move to only nearby locations. Synthetic dimensions replicate this locality using nonspatial degrees of freedom, which may offer greater flexibility for engineering and measurement, as compared to spatial dimensions. Researchers have previously taken advantage of these benefits by implementing synthetic dimensions on a number of platforms, which they have used to study exciting physics, including spin-orbit coupling and a multitude of topological phenomena [2, 3].

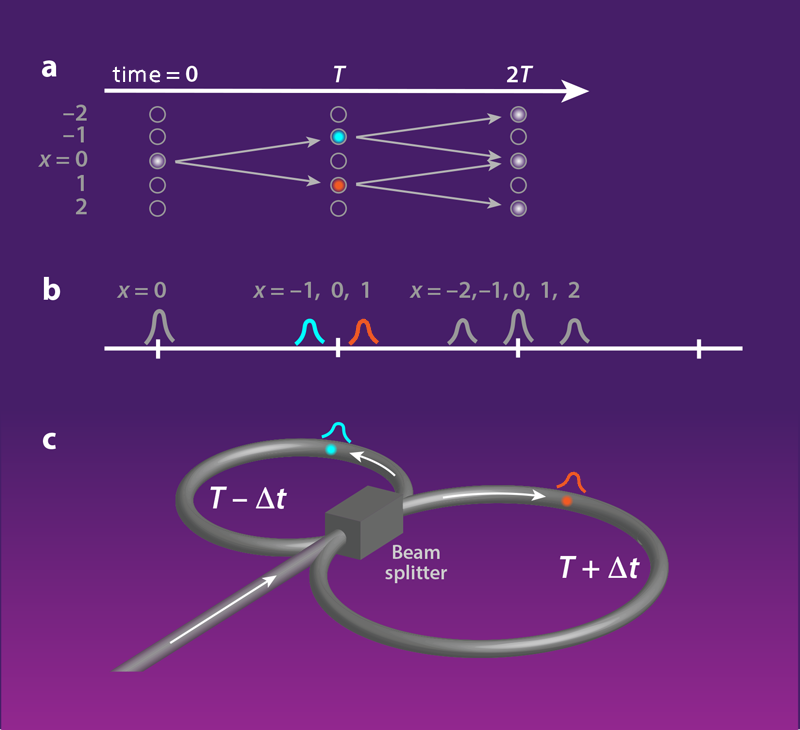
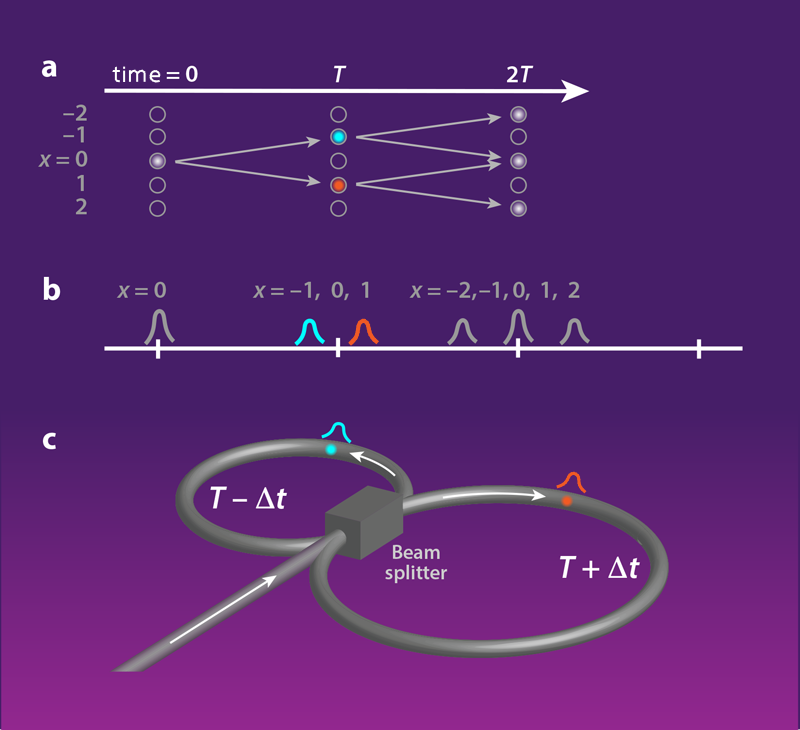
To realize a synthetic dimension for light, Wimmer and colleagues use an optical mesh lattice: an experimental setup in which the arrival times of light pulses serve as the analog of position (Fig. 1). In their experiment, time is divided into intervals $T$ , and each interval represents a discrete time step, $t = 1, 2, \dots$ . Discrete positions corresponding to sites on a lattice $(x = \dots, - 2, - 1, 0, - 1, 2, \dots)$ are mapped onto this time sequence as subintervals separated from each other by $Δ t$ . A pulse arriving at $T$ represents the lattice position $x = 0$ , for example, while a pulse at $T - Δ t$ represents $x = - 1$ . Moving from one lattice position to another (for example, from $- 1$ to $- 2$ ) corresponds to a change in the arrival time of the light pulse relative to $T$ (in this case, from $T - Δ t$ to $T - 2 Δ t$ ). This process mimics motion in real space: as a particle can only move in space by passing through nearby points, its analog in the synthetic dimension can move only to nearby lattice sites.

To implement such motion in the synthetic dimension, the researchers join two loops of fiber-optic cable of slightly different lengths via a beam splitter. Light propagates around the short loop in time $T - Δ t$ and around the long loop in $T + Δ t$ . Therefore, a light pulse at synthetic position $x$ and synthetic time step $t$ will be shifted to $x - 1$ or $x + 1$ at time step $t + 1$ if it passes through the short or the long loop, respectively. After a pulse completes a loop, the beam splitter splits it into two equal parts that continue on through both loops.

While this synthetic motion isn’t in and of itself very interesting, the specific physical system in which the synthetic dimension is realized allows powerful capabilities. Here, the nonlinear dielectric response of the fiber used in the experiment produces a power-dependent phase shift, meaning that multiple light pulses interact when they overlap within a loop. These interactions change the system’s behavior from that of an ideal gas into one with fluid-like properties. Optical mesh lattices exhibiting such light-light interactions have previously been used to study phenomena such as solitons [4, 5] and non-Hermitian topological effects [6–8], but fluid properties arising from interactions and motion—in particular, superfluid-like flow—have not been observed until now.

Wimmer and colleagues measure the speed of “sound” in this fluid of light, where sound refers to waves that propagate in the synthetic dimension. Their technique is similar to dropping a stone in a pond: by repelling some of the pond’s water, the stone excites ripples, which spread at the speed of water waves. In this experiment, the “pond” is a roughly homogeneous fluid spanning about ten synthetic sites; the “stone” is a repulsive force that the researchers generate around a couple of sites at the center of the fluid. This repulsive force produces ripples of light that propagate outward in the synthetic dimension at the light superfluid’s speed of sound. Measurements of how the ripples propagate agree qualitatively (with some deviations likely due to experimental imperfections) with hydrodynamic theory. Specifically, the light acts like a superfluid, which passes across obstacles without dissipation.

To further explore the properties of this superfluid, Wimmer and colleagues drag an “obstacle” through it. More precisely, they oscillate the position of a localized potential-energy well and measure the energy that this deposits in the fluid. In an ordinary fluid, energy would be deposited whatever the velocity of the obstacle, whereas in a superfluid, dissipation only occurs above a so-called critical velocity. Indeed, the researchers observe this behavior in their synthetic superfluid: for sufficiently slow oscillations, the potential energy is unchanged, while for oscillations faster than a critical oscillation rate, energy is transferred to the fluid. The broad agreement between the measured and predicted critical velocities confirms the superfluid interpretation.

These results demonstrate the opportunities afforded by engineering light interactions in optical mesh lattices. The tunable interaction strength, together with the spatial and temporal control of the potential energies and of the lattice geometry, makes this platform extremely versatile. The superfluid physics observed by Wimmer and colleagues is a beautiful example of how this versatility can be harnessed to make light behave in a novel and interesting way. In the future, a similar technique may be used to explore nonlinear band structures such as swallowtails [9], the interplay of condensate with thermal excitations, and the behavior of interacting Bose condensates in the presence of topology or dissipation.

An intriguing (though more speculative) direction would be to extend these experiments to the quantum regime, where photons—individual quanta of the light field—are relevant. In this regime, the experiments could serve as quantum simulators, able to mimic physical systems that are intractable for classical computers, or they might be able to generate quantum states that could be harnessed in sensing devices that outperform any classical device. While the technical challenges for reaching the quantum regime are daunting, I have watched experimentalists overcome daunting challenges time and time again. Whatever directions experiments take, optical fluids in synthetic dimensions of optical mesh lattices provide rich phenomena for physicists to explore.

References

M. Wimmer et al., “Superfluidity of light and its breakdown in optical mesh lattices,” Phys. Rev. Lett. 127, 163901 (2021).
T. Ozawa and H. M. Price, “Topological quantum matter in synthetic dimensions,” Nat. Rev. Phys. 1, 349 (2019).
T. Ozawa et al., “Topological photonics,” Rev. Mod. Phys. 91, 015006 (2019).
A. L. M. Muniz et al., “2D solitons in $𝓟 𝓣$ -symmetric photonic lattices,” Phys. Rev. Lett. 123, 253903 (2019).
M. Wimmer et al., “Observation of optical solitons in PT-symmetric lattices,” Nat. Commun. 6, 7782 (2015).
C. Chen et al., “Observation of topologically protected edge states in a photonic two-dimensional quantum walk,” Phys. Rev. Lett. 121, 100502 (2018).
H. Chalabi et al., “Synthetic gauge field for two-dimensional time-multiplexed quantum random walks,” Phys. Rev. Lett. 123, 150503 (2019).
S. Weidemann et al., “Topological funneling of light,” Science 368, 311 (2020).
E. J. Mueller, “Superfluidity and mean-field energy loops: Hysteretic behavior in Bose-Einstein condensates,” Phys. Rev. A 66, 063603 (2002).

About the Author

Kaden Hazzard is an associate professor of physics at Rice University, Texas. He received his Ph.D. in 2010 from Cornell University, New York, after which he completed a postdoctoral fellowship at JILA, Colorado. He is a theorist interested in quantum many-body systems, especially in ultracold matter. His group works at the locus of ultracold systems, condensed matter, and quantum information. Ongoing research includes novel quantum simulations using atomic, molecular, and optical systems, synthetic dimensions, exactly solvable models, and exotic matter. For more information, visit https://kaden.rice.edu/