Measuring the Neutron Lifetime with Record-Breaking Precision

Shannon F. Hoogerheide

Viewpoint

Measuring the Neutron Lifetime with Record-Breaking Precision

National Institute of Standards and Technology, Gaithersburg, MD, USA

October 13, 2021• Physics 14, 142

An improved version of a “bottle” experiment lets researchers lower the uncertainty on this important parameter—but a tantalizing discrepancy remains.

Figure caption — **Figure 1:** A cartoon image of the UCN $𝜏$ Collaboration’s experiment. A known quantity of ultracold neutrons (blue cloud) is held in a magnetogravitational trap (asymmetric pink bowl) for a specified period. During that period, some neutrons undergo beta decay (inset). At the end of the period, a detector (grey sheet) is lowered into the trap to count how many neutrons remain.

Outside of atomic nuclei, neutrons decay quickly into other particles, with an average lifetime $𝜏_{n}$ of approximately 15 minutes. Obtaining a precise value for $𝜏_{n}$ has potentially far-reaching consequences for our understanding of the Universe, as it offers a way to test important details of the laws of physics that are relevant to particle physics, astronomy, and cosmology. Now, with an experiment at the Los Alamos Neutron Science Center (LANSCE) in New Mexico, the $UCN 𝜏$ Collaboration has achieved the most precise measurement of $𝜏_{n}$ to date [1]. At 877.75 s, with a total uncertainty of 0.039%, this measurement has less than half the uncertainty of the previous best experiments—one conducted by the same group [2] and one from a European collaboration [3].

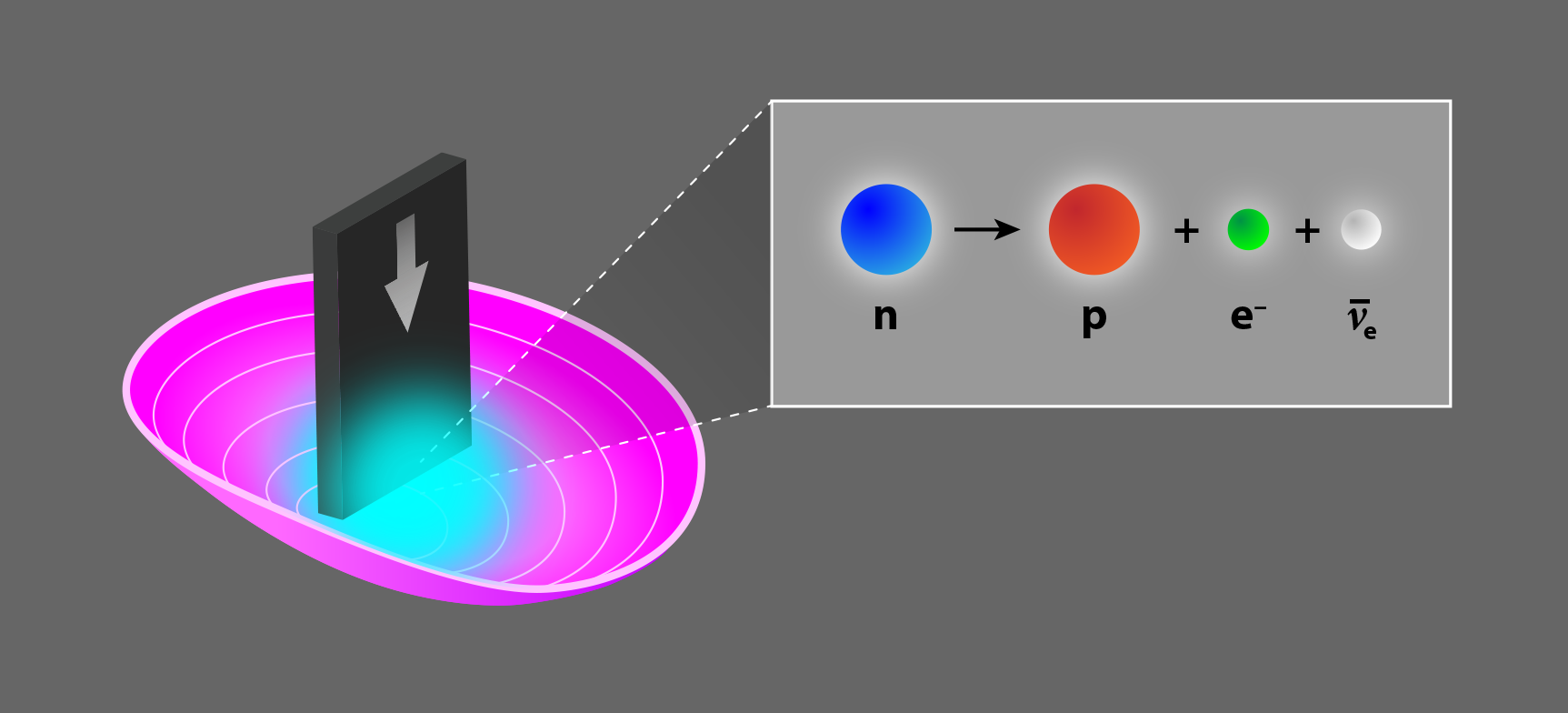
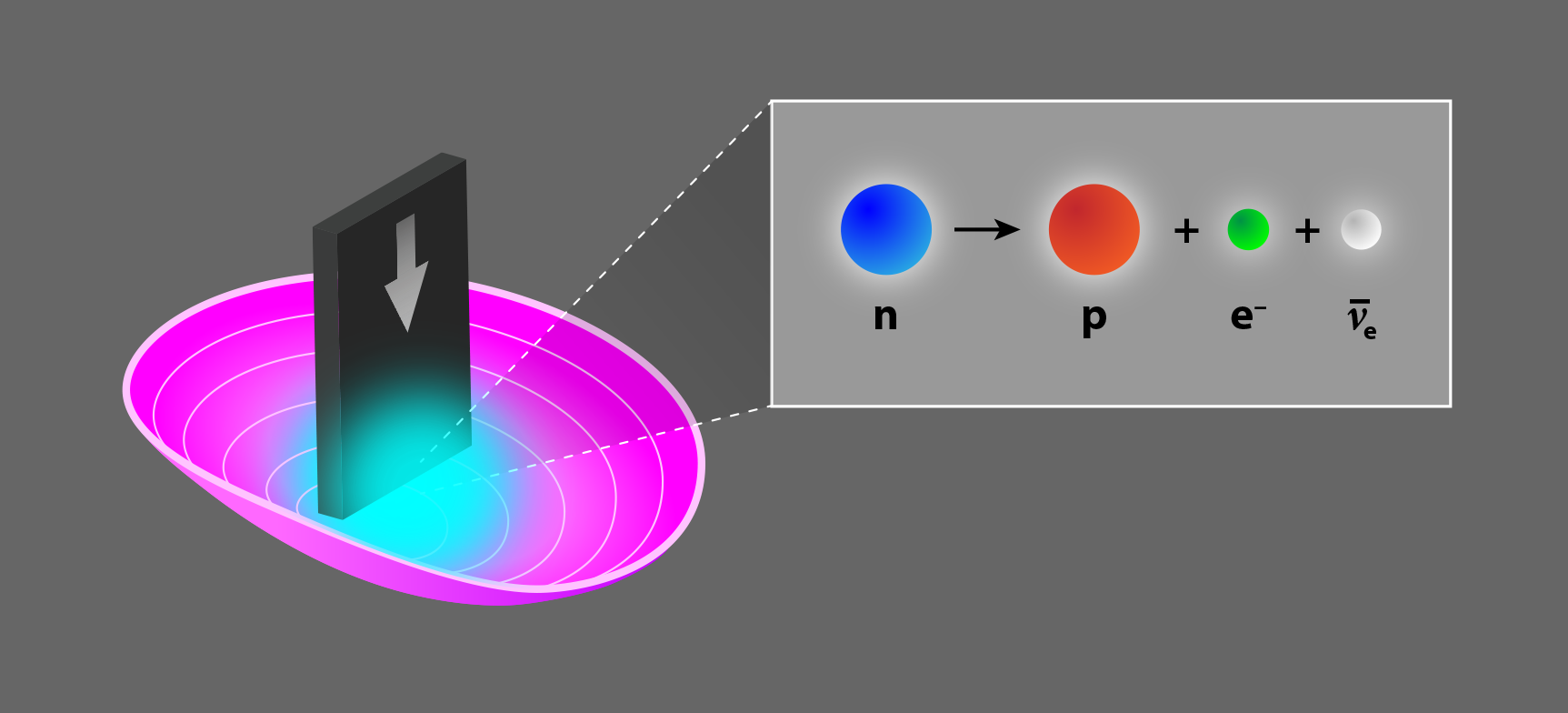
The new measurement was made using a so-called bottle experiment, in which a trap (the “bottle”) is filled with a known number of ultracold neutrons (UCNs). By counting how many neutrons remain after a certain interval, the neutron decay rate, and therefore the average neutron lifetime, can be calculated. One of the challenges in performing this measurement is that the neutron lifetime is long. Although 15 minutes might seem like a manageable interval, achieving a sufficient number of decays to reach the required statistical precision in a practical amount of time requires the confinement of large numbers of particles. Further challenges include slowing down, or moderating, the neutrons (reactors or spallation sources generate neutrons with several-hundred-MeV energies, whereas trapping requires neutrons with energies of a few hundred neV), controlling neutron losses, and evening out fluctuations in the stored UCN energy spectrum.

These challenges have been managed to some extent during earlier measurements conducted at LANSCE, but the new experiment reduces the uncertainty deriving from these effects to an unprecedentedly low level. The researchers use a setup that is similar to their previous experiments, in which UCNs at approximately 180 neV are polarized so that they seek magnetic-field minima before being fed into a magnetogravitational trap—an open-topped bowl made of permanent magnets arranged in a so-called Halbach array (Fig. 1). The UCN sample is then “cleaned,” meaning the particles with the highest energy are either captured by boron-10-coated ZnS surfaces or scattered out of the trap. This cleaning process is important to ensure the trap contains only the lowest-energy UCNs, which have little chance of escaping during the storage period. Any escaping neutrons could lead to an error in the determination of $𝜏_{n}$ . After cleaning, the UCNs are stored in the trap for 20–1550 s and then counted.

The new study differs from previous experiments in the addition of a buffer volume between the neutron source and the trap in which the UCNs are held before the storage period begins. This buffer flattens the energy distribution of the UCNs by minimizing the effects of source fluctuations, and it serves as an additional cleaning stage.

A further difference comes at the end of the storage period. Whereas other UCN bottle experiments dumped the UCNs out of the trap so that they could be counted at a separate detector, the $UCN 𝜏$ Collaboration utilizes an in situ detector that can be lowered into the trap in stages. Not only does this technique eliminate the possibility of incurring losses while the UCNs are transported to the detector, but it also allows the team to map out the energies and trajectories of the UCNs by taking measurements at different heights. This additional information provides a way of checking for systematic particle losses.

The $UCN 𝜏$ researchers also improved the way they analyze their data. In their latest study, they use three independent, blinded analyses to reduce the contributions of all systematic effects, of abnormal running conditions and unphysical data points, and of statistical biases. Each analysis determines $𝜏_{n}$ by two different methods: a “paired” analysis, which averages the short- and long-storage-time runs, and a “global” analysis, which uses a maximum likelihood fit over all acquired data. The results of the blinded analyses are compared, and the data are unblinded only when the three $𝜏_{n}$ values agree to within 0.1 s. The final result for $𝜏_{n}$ comes from an unweighted average of the central values from the three analyses.

As a result of these experimental and analytical improvements, the researchers have been able to reduce the effect of all known systematics to the level where the few corrections that must be applied are smaller than the experiment’s overall uncertainty. The resulting precision could help to shape our most fundamental theories. For example, the neutron lifetime is one of the inputs used to calculate the abundance of helium-4 in the early Universe due to big bang nucleosynthesis (BBN) [4]. Combining BBN calculations with astronomical observations therefore offers a powerful probe of new physics.

An analysis of $𝜏_{n}$ in combination with other properties of neutron beta decay can also be used to test the standard model. For example, such an analysis can help to reduce the uncertainty in the value of the weak axial vector coupling constant, which governs processes involving charged weak interactions including BBN, neutron star formation, solar fusion, and (anti)neutrino detection. The standard model predicts that this parameter, together with the vector coupling constant, fully describes such interactions, while some beyond-the-standard-model theories require additional scalar and tensor terms, which would in turn affect the value of $𝜏_{n}$ . A combined analysis can also determine an important parameter describing the weak interaction called the quark mixing matrix element $V_{u d}$ . The current best value for $V_{u d}$ comes from observing a set of nuclear beta decays involving complex nuclei, but such derivations demand nuclear-structure corrections. These corrections are unnecessary for free-neutron decay, so extracting this parameter from $𝜏_{n}$ may be more reliable. The $UCN 𝜏$ Collaboration’s new result means that free-neutron determinations of $V_{u d}$ are nearly competitive with those from superallowed nuclear decays, giving physicists yet another handle in their quest for new physics.

As impressive and important as this result is, it should be noted that the improved precision is insufficient to resolve a lingering discrepancy affecting neutron-lifetime measurements. Bottle experiments like that conducted by the $UCN 𝜏$ Collaboration, in which the remaining neutrons are counted, represent just one way of measuring $𝜏_{n}$ . This value can also be measured by observing the products of neutron beta decay in a cold-neutron beam. On average, these beam experiments yield a value for $𝜏_{n}$ about 8 s longer than that indicated by bottle experiments [5]. On its own, the $UCN 𝜏$ Collaboration’s new result doesn’t close this gap (the uncertainty in both types of experiments was already much smaller than 8 s). Eliminating the discrepancy will require new complementary measurements such as those utilizing the beam method, measurements that combine both beam and bottle methods, or even novel space-based techniques [6]. Fortunately, many experiments are underway or in development to do just that [7].

References

F. M. Gonzalez et al. (UCNτ Collaboration), “Improved neutron lifetime measurement with UCN $𝜏$ ,” Phys. Rev. Lett. 127, 162501 (2021).
R. W. Pattie et al., “Measurement of the neutron lifetime using a magneto-gravitational trap and in situ detection,” Science 360, 627 (2018).
A. Serebrov et al., “Measurement of the neutron lifetime using a gravitational trap and a low-temperature Fomblin coating,” Phys. Lett. B 605, 72 (2005).
R. H. Cyburt et al., “Big bang nucleosynthesis: Present status,” Rev. Mod. Phys. 88, 015004 (2016).
G. L. Green and P. Geltenbort, “A puzzle lies at the heart of the atom,” Sci. Am. 314, 36 (2016).
D. J. Lawrence et al., “Space-based measurements of neutron lifetime: Approaches to resolving the neutron lifetime anomaly,” Nucl. Instrum. Methods Phys. Res. A 988, 164919 (2021).
D. Dubbers and B. Märkisch, “Precise measurements of the decay of free neutrons,” Annu. Rev. Nucl. Part. Sci. 71, 139 (2021).

About the Author

Shannon Hoogerheide is a staff physicist in the Neutron Physics Group at the National Institute of Standards and Technology (NIST). Her research focuses on precision measurements of fundamental physics using neutrons, including experiments to measure the neutron lifetime and the spin rotation of polarized neutrons. She is also involved in neutron interferometry, detector development, and neutron irradiations and calibrations. She received a B.S. in Physics from Calvin College and an A.M. and a Ph.D. in Physics from Harvard University, where she worked on measurements of the electron and positron magnetic moments. Prior to joining the Neutron Physics Group, she was a National Research Council Postdoctoral Fellow in the Atomic Spectroscopy Group at NIST where she worked with highly charged ions.