A Third Way to Explain Fine Tuning
What do the Higgs mass and Earth’s orbit ellipticity have in common? Both have values that are orders of magnitude smaller than theoretical estimates would suggest. These quantities appear to result from an extremely fine-tuned cancellation of two much larger quantities—a fact that many physicists find implausible (Fig. 1). These and other “fine tunings,” however, might only be apparent, and their explanation may hold the key for paradigmatic changes in our understanding of nature. Particle physics features two of the most intriguing fine-tuning puzzles: the Higgs boson mass and the cosmological constant.
For a long time, the lore had it that these particle-physics tunings may be related to new symmetries, such as the elusive supersymmetry, or to statistical arguments—our fine-tuned Universe is just one of many possible multiverses. In recent years, however, new possible explanations have emerged [1–5], culminating in a new proposal by Nima Arkani-Hamed of the Institute for Advanced Study, New Jersey, Raffaele Tito D’Agnolo of the University of Paris-Saclay, and Hyung Do Kim of Seoul National University [6]. The trio identified a new class of mechanisms for producing fine tunings, in which only specific values of the Higgs mass can “trigger” the formation of multiverses. The appeal of their model is that it makes testable predictions—the existence of new, potentially observable Higgs particles.
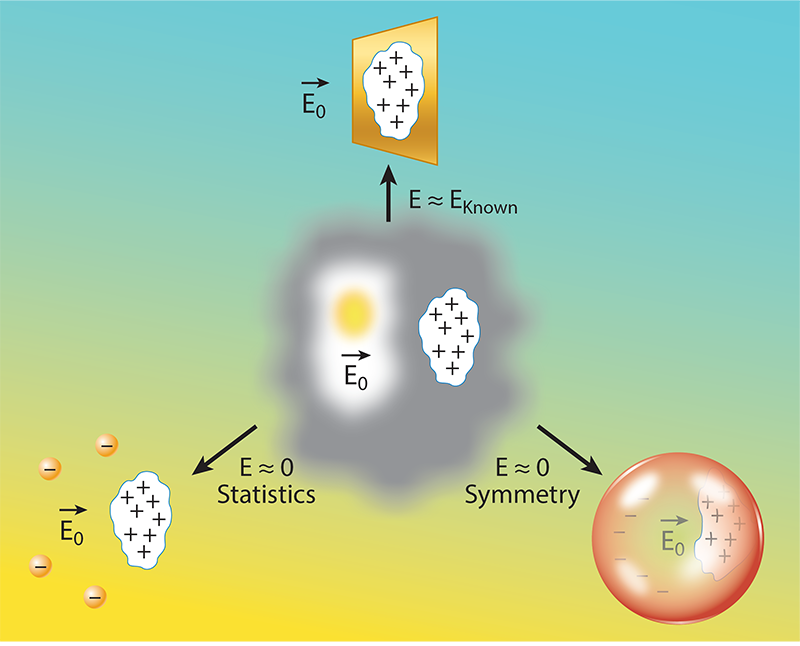
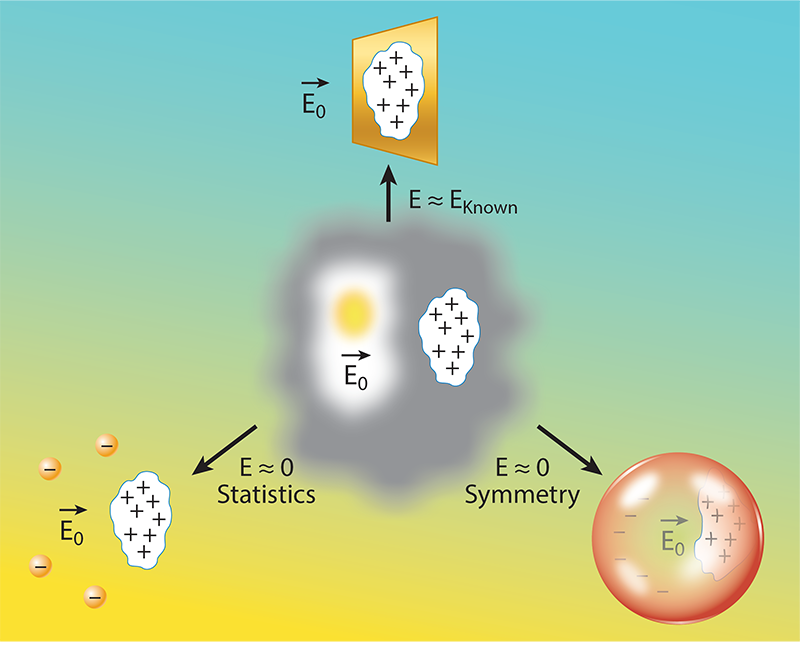
To understand fine tuning, consider a measurable quantity that could be theoretically computed were it not for the fact that the necessary information is partially unavailable. Take, for example, the electric field near a charged conducting surface of which we can observe only a small region (Fig. 2). The field can be computed from the known charges in this region but may be affected by other, unknown charges. The observed value will be the sum of a known and unknown contribution. An observed value close to that derived from the known contribution would indicate that the unknown contribution isn’t significant, and the difference may have a trivial explanation, such as some unaccounted-for difference in the conductor’s geometry.
But if the observed value is much smaller than that expected from the known contribution, it means that the known and unknown parts almost exactly cancel out. Often, this fine tuning reveals something new about the system. For instance, the conducting surface could extend to form a closed shell, or “Faraday shield,” inside which the electric field is zero. In this case, the tuning results from the symmetries of electromagnetism. It could also be that oppositely charged point particles are distributed so as to precisely cancel the electric field. This canceling could just be a statistical fluke—a chance arrangement that only occurs in one out of many possible experiments.
Similar examples abound in science. The mass of the electron appears to be fine tuned when one considers the large amount of energy that, according to classical electromagnetism, is stored in the electric field around the particle. But the explanation comes from a “new” particle, the positron, which influences the electron’s mass through the effect of fleeting electron-positron pairs generated in the quantum-mechanical vacuum around the electron. The low eccentricity of Earth’s orbit is an example of an apparent fine tuning that can be explained statistically: Earth is just one among myriad exoplanets whose orbits’ eccentricities are suitable for life to develop. In both cases, the apparent fine tunings were resolved by disruptive scientific discoveries—the discovery of the positron and of exoplanets.
Other fine tunings, however, still puzzle physicists, such as those found in the standard model of particle physics. The standard model has unparalleled predictive power, but two of its parameters—the Higgs mass and the cosmological constant—appear to be extremely precisely tuned: To obtain the relatively small observed values of these two parameters, physicists require additional, unknown contributions that can almost exactly cancel other extremely large contributions from physics at scales that are accurately described by the standard model. If the standard model were to be valid up to the Planck scale, these additional contributions must be tuned to one part in 1034 for the Higgs and to one part in 10120 for the cosmological constant. Could these tunings also be signposts to conceptual breakthroughs? Concocting testable explanations has been a goal of theoretical physicists for the past four decades.
Traditional solutions fit in two categories: a so-called dynamical explanation and a multiverse explanation. The dynamical option implies new structure, particles, or symmetries, such as supersymmetry—a theory in which the equations for matter and forces are identical—or Higgs compositeness—a theory in which the Higgs boson is a bound state of new strong interactions. The multiverse solution, on the other hand, provides a statistical explanation of why the observed cosmological constant is so small: We just happen to inhabit the one “anthropic” Universe among 10120 possible universes whose cosmological constant enables life [7]. But observations have so far failed to deliver evidence for either the dynamical or the multiverse explanation, so researchers are starting to consider alternative scenarios.
The third route explored by Arkani-Hamed, D’Agnolo, and Kim combines both dynamics and multiverses. Imagine a system whose energy spectrum depends on a parameter and exhibits—for special values of this parameter—a multiplicity of nearly degenerate ground states (a situation similar to that encountered in condensed-matter experiments, where the potential energy can be easily tweaked via experimental knobs). The researchers consider a particle-physics system where the special parameter is the Higgs mass. They show that this scenario requires the notion of “triggers”: certain couplings of the Higgs to other particles or forces that would cause the Higgs mass to affect other physical observables. In this scenario, nearly degenerate states—in this case, multiverses—only emerge for specific Higgs mass values. These triggers address both fine tunings at once because the multiverse allows for the existence of an anthropic universe. Unlike the original multiverse solution, however, triggers are falsifiable, as they are associated with new couplings or new particles that can be searched for. And unlike dynamical solutions, triggers don’t imply new forms of symmetry that have so far eluded detection.
The trio’s calculations show that there are only a handful of possibly relevant triggers (in the standard model but also, surprisingly, in theories that extend the standard model) and that the theory can deliver precise predictions for each trigger possibility. The most interesting trigger possibility involves the existence of further Higgs particles (a two-Higgs doublet model) with masses at or below the known Higgs boson mass (125 GeV). Such a scale is within reach of collider experiments, including those involving rare B-meson decays at the LHCb experiment or top decays at CERN’s ATLAS and CMS experiments. There is still a large portion of parameter space that is amenable to exploration, and the new theory of triggers pinpoints promising search targets whose discovery would require much more than a “tuning” of our scientific theories.
References
- L. F. Abbott, “A mechanism for reducing the value of the cosmological constant,” Phys. Lett. B 150, 427 (1985).
- G. Dvali and A. Vilenkin, “Field theory models for variable cosmological constant,” Phys. Rev. D 64, 063509 (2001).
- P. W. Graham et al., “Cosmological relaxation of the electroweak scale,” Phys. Rev. Lett. 115, 221801 (2015).
- A. Arvanitaki et al., “A small weak scale from a small cosmological constant,” J. High Energ. Phys. 2017, 71 (2017).
- J. R. Espinosa et al., “Cosmological Higgs-axion interplay for a naturally small electroweak scale,” Phys. Rev. Lett. 115, 251803 (2015).
- N. Arkani-Hamed et al., “Weak scale as a trigger,” Phys. Rev. D 104, 095014 (2021).
- S. Weinberg, “Implications of dynamical symmetry breaking: An addendum,” Phys. Rev. D 19, 1277 (1979).