The Tiniest Superfluid Circuit in Nature

Piotr Magierski

Viewpoint

The Tiniest Superfluid Circuit in Nature

Faculty of Physics, Warsaw University of Technology, Warsaw, Poland
Department of Physics, University of Washington, Seattle, WA, USA

February 25, 2021• Physics 14, 27

A new analysis of heavy-ion collision experiments uncovers evidence that two colliding nuclei behave like a Josephson junction—a device in which Cooper pairs tunnel through a barrier between two superfluids.

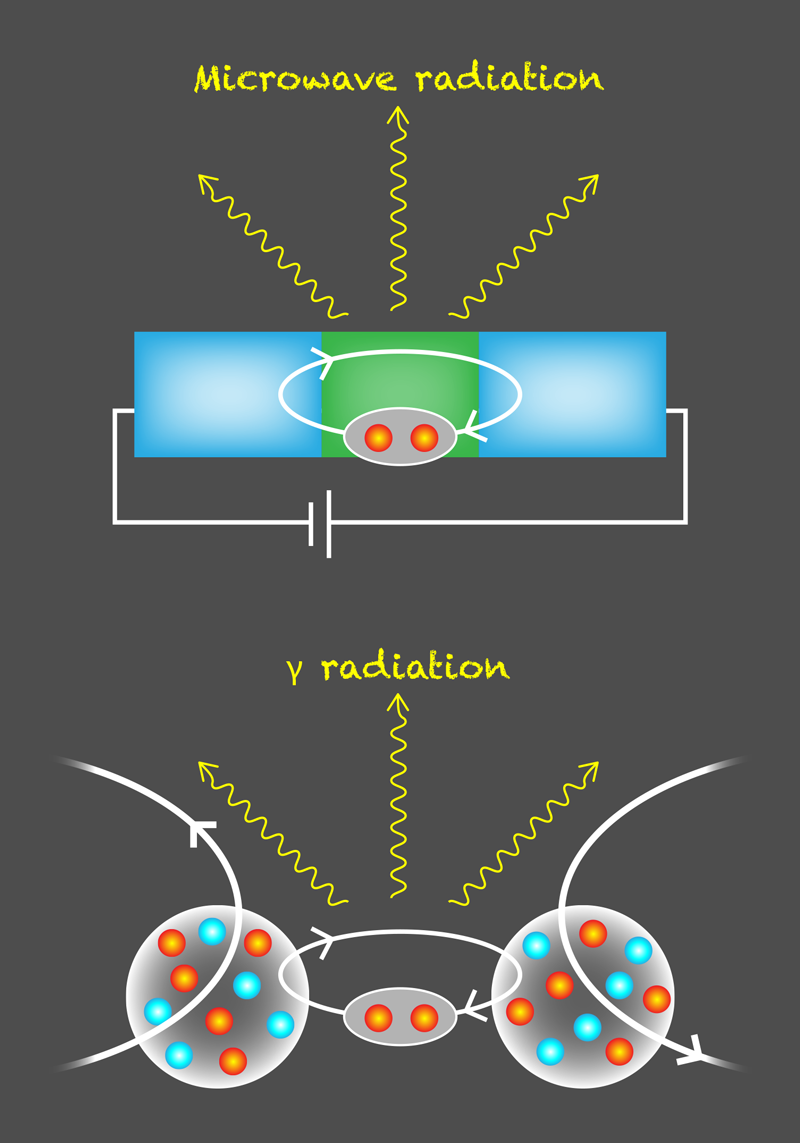
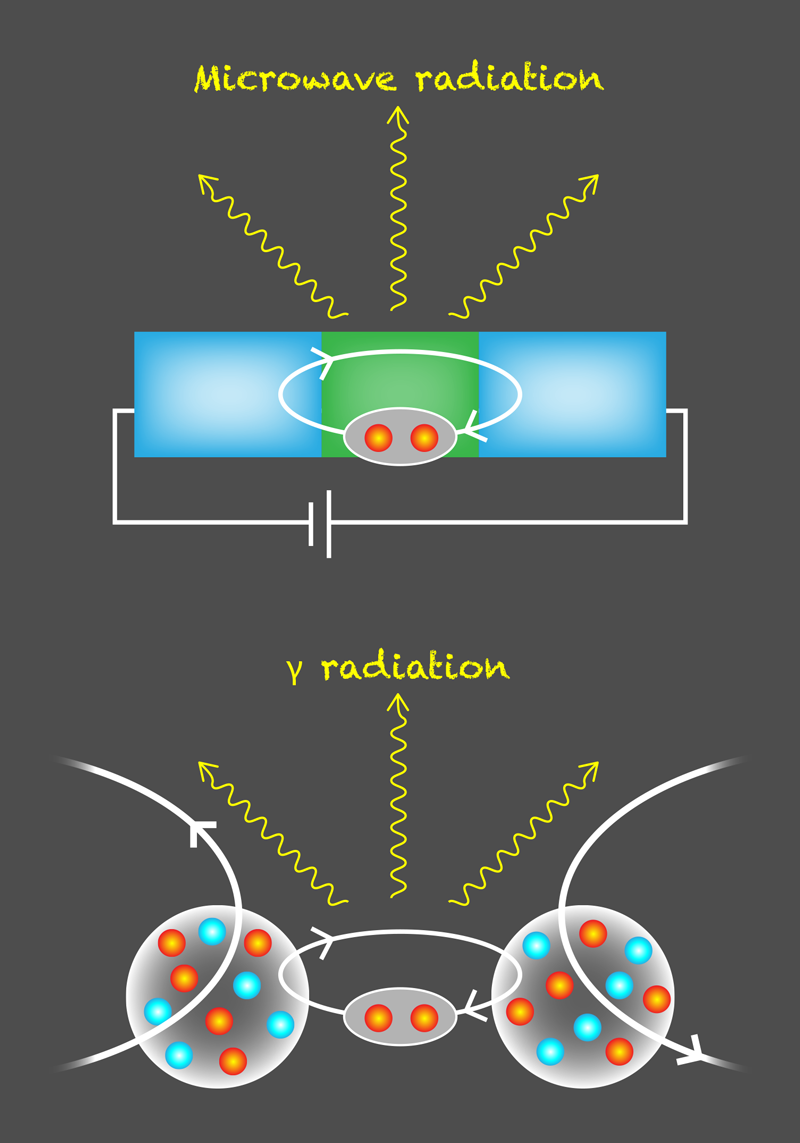
Figure caption — **Figure 1:** (Top) Sketch of a Josephson junction, in which Cooper pairs tunnel through a barrier (green) between two superconductors (blue). In the ac Josephson effect, an applied dc voltage produces an oscillating, or ac, current, leading to the emission of microwave photons. (Bottom) Potel and co-workers have shown that a similar description applies to colliding nuclei [4]. As the nuclei approach, neutron pairs tunnel back and forth between them, causing the emission of gamma-ray photons.

The Josephson effect is a remarkable example of a macroscopic quantum phenomenon, in which, without an applied voltage, current flows between two superconductors separated by a thin film of normal material. In this structure, called a Josephson junction, the current is due to the quantum tunneling of paired, superconducting electrons (so-called Cooper pairs) [1]. For decades, nuclear physicists have hypothesized that similar effects can occur on much smaller scales, since atomic nuclei could be regarded as superfluids consisting of paired nucleons. Recent experiments have supported this hypothesis, delivering hints that two colliding nuclei could be described as a Josephson junction in which entangled neutron pairs play the role of Cooper pairs (Fig. 1) [2, 3]. Now, Gregory Potel from Lawrence Livermore National Laboratory in California and colleagues have put these ideas on firmer ground [4]. Analyzing tin-nickel collisions from previous experiments, they found that experimental observables offer compelling signatures that two nuclei indeed form, for a split second, a Josephson junction.

The orderly motion of gigantic ensembles of correlated electron pairs makes superconductors behave as a single object—a macroscopic quantum state called a condensate. The condensate is characterized by its density and phase, and the latter plays the same role as the orientation of magnetic moments in a ferromagnet: an isolated ferromagnet can be rotated at no energy cost, but two ferromagnets with different orientations affect each other. Similarly, according to quantum mechanics, the phase doesn’t have implications for a single condensate. But if two condensates are sufficiently close, a Cooper-pair current, whose magnitude depends on the phase difference, may flow from one condensate to the other. A striking feature of this effect is that electric current may flow without a driving voltage.

There may be other systems in Nature where this effect occurs, and atomic nuclei, which can be regarded as superfluid ensembles of nucleons, are good candidates. This idea appeared among nuclear physicists as early as the 1970s [5]. In the 1980s and 1990s, several experiments indicated an enhanced probability of neutron-pair transfer between colliding nuclei—a possible manifestation of the Josephson effect. But the evidence for this interpretation wasn’t compelling. There were doubts, in particular, about whether ensembles of nucleons are sufficiently large to be treated as a pair condensate. Superconductivity is an emergent phenomenon: It appears when dealing with a huge number of particles but vanishes when the system is broken down into smaller constituents. But can we consider a nucleus made of about 100 nucleons a huge ensemble of particles? Can we expect that two nuclei in close proximity exhibit a Josephson effect?

The study by Potel and his colleagues provides strong arguments for affirmative answers to these questions. The researchers analyzed data from previous experiments in which tin-116 ( $^{116} Sn$ ) nuclei were collided with nickel-60 ( $^{60} Ni$ ) [2]. With energies between 140.60 and 167.95 MeV, these collisions are “gentle”: they allow the nuclei to overcome just enough of the Coulomb repulsion to get sufficiently close to exchange a few neutrons at most. Under such conditions, two reactions are possible: the transfer of one neutron and the transfer of two neutrons, producing $^{115} Sn +^{61} Ni$ and $^{114} Sn +^{62} Ni$ , respectively. The case of two-neutron transfer is particularly interesting, as it may carry signatures of the correlated pairing of neutrons in the nuclei.

The team devised a way to uncover the experimental evidence of Josephson flow. Their idea is that there can be a nuclear equivalent of the alternating current (ac) Josephson effect (Fig. 1). In this variant of the Josephson effect, a constant, or dc, voltage applied to a Josephson junction produces an ac current. This striking behavior arises because the voltage causes the phase difference between the two condensates to increase over time. Since phases that differ by multiples of $2 𝜋$ are equivalent, a linear phase growth produces an oscillating current. The researchers argue that for the nuclear case, a similar effect can occur because neutron pairs inside two colliding nuclei possess different energies. This energy difference plays the role of the dc voltage in the ac Josephson effect.

Therefore, similar oscillatory behavior is expected to occur during a nuclear collision: the back-and-forth tunneling of neutron pairs means that $^{116} Sn +^{60} Ni$ transforms into $^{114} Sn +^{62} Ni$ and then again into $^{116} Sn +^{60} Ni$ —a cyclical process whose frequency is determined by the energy difference of neutron pairs in initial and final nuclei. Because the collision lasts for only a short time, the team estimates that only about three such back-and-forth transfer cycles may occur in an experiment. However, even these few oscillations can lead to observable consequences. Since neutrons and protons interact strongly, oscillating neutron pairs cause protons to oscillate at the same frequency. Because of their charge, oscillating protons should emit electromagnetic radiation at this frequency. While electrons oscillating in a standard Josephson junction emit microwave photons [6], nuclei are expected to emit gamma-ray photons because of the much larger nuclear energy differences involved. The researchers calculate the expected radiation energy to be slightly less than 4 MeV, which matches the gamma-ray spectrum seen in previous experiments.

The results are thrilling for two reasons. First, they indicate that the principles of superconductivity valid for macroscopic phenomena in solids may be applicable to the much smaller (femtometer) nuclear scales—a truly spectacular conclusion. Second, the analysis shows that the pairing description is appropriate for a small number of particles—the hundreds of nucleons making up the nuclei. It is worth pointing out, however, that this description contains a puzzling inconsistency. According to quantum mechanics, the phase and the number of particles in the condensate are related by the uncertainty principle—much like the position and momentum of a quantum particle: if either quantity is well defined, the other isn’t. But for the nuclear case, the number of nucleons is always exactly defined. Further theoretical work will need to resolve this inconsistency.

These findings whet our appetite for more work aimed at validating superfluid nuclear models by confronting theory with experiments. In particular, it would be crucial to show that such models can deliver accurate, quantitative predictions for analogous effects in nuclear collisions beyond those involving tin and nickel.

References

B. D. Josephson, “Possible new effects in superconductive tunnelling,” Phys. Lett. 1, 251 (1962).
D. Montanari et al., “Neutron pair transfer in $^{60} Ni +^{116} Sn$ far below the Coulomb barrier,” Phys. Rev. Lett. 113, 052501 (2014).
D. Montanari et al., “Pair neutron transfer in $^{60} Ni +^{116} Sn$ probed via $𝛾$ -particle coincidences,” Phys. Rev. C 93, 054623 (2016).
G. Potel et al., “Quantum entanglement in nuclear Cooper-pair tunneling with $𝛾$ rays,” Phys. Rev. C 103, L021601 (2021).
K. Dietrich, “On a nuclear Josephson effect in heavy ion scattering,” Phys. Lett. B 32, 428 (1970).
S. Shapiro, “Josephson currents in superconducting tunneling: The effect of microwaves and other observations,” Phys. Rev. Lett. 11, 80 (1963).

About the Author

Piotr Magierski is Professor of Physics and Head of the Nuclear Physics Division at Warsaw University of Technology, Poland, and an Affiliate Professor at the University of Washington. He is a theoretical physicist whose research interests include superfluidity and superconductivity in systems far from equilibrium, such as nuclear fission and fusion reactions, nuclear matter in neutron stars, and ultracold atomic gases.