Common Ground in Avalanche-Like Events
Karin Dahmen loves noise. A theoretical physicist at the University of Illinois at Urbana-Champaign, she has spent most of her career studying the “crackling noise” emitted by different materials when they deform. The noise emitted when a piece of paper is crumpled, for example, is a series of discrete snaps that vary in loudness. If you were to plot the number of snaps for each loudness value, you would find that the curve follows a “power law” relation. Dahmen and others have found this type of distribution in a wide variety of so-called disordered materials, such as crystal shards, snowbanks, and Earth’s crust. And Dahmen has developed models that can replicate this mathematical trend and explain why it arises.
Many systems—not just disordered materials—exhibit behavior that scales with loudness, size, or some other measure. Similar power-law scaling patterns are observed in the spiking of neurons in the brain, in the dimming of the light emitted by a star, and in the spreading of a fire through a forest. Very recent studies also hint that power laws should pop up in the learning ability of artificial intelligence algorithms. “These similarities are telling us that all these different systems behave in the same ways under certain conditions and that the details of the system don’t matter,” Dahmen says. “That’s incredibly powerful.”
Dahmen and her colleagues hope to soon use the universality within disordered systems to predict—without the need for painstaking experiments—how new materials or hard-to-test systems deform, which could allow for cheaper and quicker design of materials. The possibility of converting a physics curiosity into a practical tool has others in the field excited, too. “It’s not simply about finding power laws,” says Jean Carlson, who studies earthquakes and forest fires at the University of California, Santa Barbara. “It’s about learning something that is going to be useful for solving a problem.”
A Sliding Resemblance
Compress a pillar made of a metallic glass—a material with randomly arranged atoms—and patches of atoms inside the pillar can rearrange in a series of sudden jumps. This mode of rearrangement resembles the series of slips that occurs as shifting tectonic plates rub against one another, causing earthquakes. The precipitous slide of snow in an avalanche can also be part of a series of slips. Each deformation event in the series has a certain size, with most events being small, some being of intermediate size, and a few being really big. Plot the number of events on a graph, and their distribution forms a power law. A power law distribution is different from an exponential one in that the power law’s shape looks the same if you zoom in or zoom out (by multiplying the inputs by a constant). “This [shape uniformity] tells you that the system behaves as if it has no typical length scale,” says Eduardo Jagla, a theoretical physicist at the Bariloche Atomic Centre in Argentina who studies avalanche-related problems.
Power-law scale-invariance also arises in the rearrangements of atoms that occur when a metal fork or nail is bent—a process that can produce an audible crackling sound. If the loudness distribution of snaps in the crackling sound is plotted on top of the size distribution of slips in a compressed pillar, the data are indistinguishable—the slips and snaps follow the same power law. This common trend has led physicists, including Dahmen, to suggest that these two materials belong to the same so-called universality class—a group of disparate systems that have identical macroscopic properties, regardless of their microscopic makeup.
Grouping materials this way allows researchers to simplify their models, as they don’t need to worry about the chemistry of the system or about other material-specific properties. “The models show that the scaling laws only depend on a few fundamental properties of the system, such as its symmetry, its dimensions, and maybe the range of its interactions,” Dahmen says. Any system that has those same symmetries, dimensions, and interactions should produce crackles and slips that look identical.
Physicists used to think that every system had its own unique power law, says James Sethna, a physicist at Cornell University and the former Ph.D. supervisor of both Dahmen and Carlson. “But now—and Karin has been the person who has slowly convinced me—we think that there are many systems that all exhibit the same universal behavior.” That universality is both a boon and a curse, he adds. “Universality makes things simpler: We can write one theory and keep using it over and over again. But it also makes things harder, as we have even less understanding of what makes one system different from another.”
What’s in the Model?
To develop a model, Dahmen first assumes that the material contains randomly distributed “weak” spots. In a granular material, these weak spots might be regions where the grains are less densely packed; in a crystal they could be defects. Second, she imagines that the weak spots have long-range elastic coupling. This coupling means that if one of these weak spots yields—the atoms or grains within it rearrange—the stress that is released will get transferred to other weak spots, potentially causing them to also give way. “It’s like a domino effect,” Dahmen says. The last modeling ingredient is to assume that the material sits near a so-called critical point in its phase diagram. For an equilibrium system, this point is where two phases of the material can coexist. For the nonequilibrium disordered systems that Dahmen studies, the critical point corresponds to conditions where the yielding of one weak spot would lead to a catastrophic failure of the material.
From these assumptions, Dahmen and her collaborators are able to predict the statistics and dynamics of the rearrangements, or “avalanches,” in the material. For example, they can determine the exponent in the power-law distribution of avalanches based on their size—defined by how many atoms or grains are rearranged in the event. These predictions depend on several factors, such as the symmetries, dimensions, and weak-spot coupling, which constitute the modeling inputs.
The models are demonstrating their worth. Wendelin Wright at Bucknell University in Pennsylvania has been testing the power-law predictions in the lab. In her experiments, Wright compresses a millimeter-sized pillar made of a metallic glass and monitors the crackling noise that the pillar produces. These crackles not only allow her to identify when an avalanche occurs in the material but also to estimate the size and propagation speed of the atomic rearrangements within the avalanche. “It’s very much like making a movie of an earthquake,” Wright says. She has now tested upwards of 15 statistical predictions of Dahmen’s models, with each one following the expected trend. “Without any fitting parameters, the model predicts the behaviors correctly,” Wright says.
Beyond Glasses and Grains
And it’s not just metallic glasses. Dahmen’s models match experimental data measuring avalanche-like behavior over 13 orders of magnitude, in systems ranging from nanometer-sized crystals to micrometer-sized magnets all the way to kilometers-long earthquakes. “With every data match, my confidence grows that the models work and that they are capturing the key mechanisms behind these material behaviors,” she says.
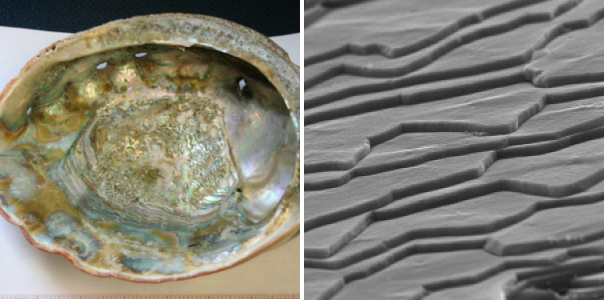
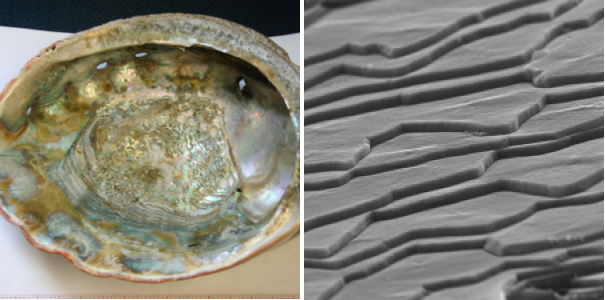
One of the latest materials to join the list is the nacre found in mollusk shells. “This material is very interesting,” says Ting Tan, a materials scientist at the University of Vermont. “Nacre should be very weak because it is made from 95% calcium carbonate—a very brittle material—but it’s actually very tough, with a strength thousands of times higher” than that of pure calcium carbonate. This strength comes from a protein-based material that glues together bricks of calcium carbonate in a wall-like structure. Applying a twisting force to a cylinder of nacre, Tan and his colleagues observed deformation behavior indicative of avalanche-like failures propagating within the shell. “The statistics and dynamics of the avalanche sizes exactly match Professor Dahmen’s predictions,” Tan says.
The agreement between theory and experiment has researchers excited that the models could be used to make deductions about other systems that are difficult or impossible to study in the lab. Sethna gives the example of boiling water: Researchers could study the liquid-vapor critical point of water by using a pressure cooker, but they haven’t because of the inherent difficulties of looking inside such a device. And they also have no need to—the amplitudes of water-molecule jiggles at the critical point follow the same scaling law as do the sizes of grain avalanches just before collapse. “The [models] allow us to study one system and make deductions about another,” Sethna says.
From the Lab to Applications
Wright thinks materials scientists could make similar deductions to predict the behavior of new materials. For example, one major goal in the metallic-glass field is finding new glass varieties that are resistant to large deformations. Techniques exist to fabricate almost any metallic glass, but rigorously testing the material properties of the vast number of possible glasses is unfeasible, she says. “If we could just take a few measurements on a glass and use them to predict its properties, that could be incredibly useful,” Wright says. Her measurements and Dahmen’s models suggest that this strategy could be successful.
Wright also thinks that the models could be used to help predict when a material is about to fail. Doing that could involve, for example, monitoring the number and sizes of slip events, which the models show should exhibit a sudden rise just before the material cracks and breaks apart. Others, however, are dubious that this predictive capability exists. “I’m not convinced that we could look at the statistics of the different events and decide based on those statistics whether or not the material will catastrophically fail,” says Craig Maloney, a computational physicist at Northeastern University in Massachusetts who studies avalanches in disordered materials. Maloney notes that power-law scaling only holds when the material is near its critical point—a regime unlikely to be of wide technological importance. “It’s unclear if the models are valid far from this regime,” he says.
That makes understanding when a model breaks down equally as important as knowing when it holds, something researchers such as Kirsten Martens are studying. A theoretical physicist at the University of Grenoble in France, Martens is picking apart the avalanche models to find out their validity limits. “It’s interesting to see that there’s so many similar behaviors, for example, in the deformation of granular systems, but there are also differences,” Martens says. For her, “understanding those differences is where the real interest and impact lies.” Lisa Manning from Syracuse University, New York, agrees. Manning studies scaling laws in biological tissues. “When the scaling laws don’t fit, that points to things that we’re missing in the models,” she says. “So it can be very powerful to ask the question: If so many things give you a scaling law, how do you break it?”
–Katherine Wright
Katherine Wright is the Deputy Editor of Physics Magazine.