Imaging an Elusive Electronic Transition in Graphene
Imagine a breeze of moist air condensing into water drops and dripping down on a cold glass. Electrons can undergo a transition that resembles this gas-to-fluid condensation: the transition is controlled by temperature and produces a fluid-like state in which electrons display remarkably different dynamics than in the gas-like state. Unlike the condensation of water vapor, however, the electron transition cannot be directly imaged with a camera. One reason for this difficulty is that the pattern of this electron fluid varies at submicron scales that can’t be clearly resolved by visible light. Another reason is that electron collisions and the redistribution of electron currents do not yield a change of surface morphology that can be picked up by light reflection. This imaging challenge has so far limited our microscopic understanding of these types of electronic transitions and their use in practical devices. Now, Alec Jenkins from the University of California, Santa Barbara, and colleagues have directly imaged the transition of electrons from a diffusive, gas-like state to a viscous, fluid-like state using a special microscope exploiting nitrogen-vacancy (NV) centers in diamond (Fig. 1) [1].
In most solid-state conductors, electrons, when placed in an electric field, flow like a gas. This gas-like motion arises from various types of scattering. Specifically, free electrons collide with lattice defects and with thermal vibrations of the ion lattice (known as phonons) while interacting only weakly with each other. Such scattering results in a current density that is proportional to the electric field—a behavior captured by the celebrated Ohm’s law. However, when electron-electron interactions become sufficiently strong, the motion of each electron is no longer independent of that of other electrons, which leads the electrons to exhibit a viscous-liquid-like behavior governed by hydrodynamic laws [2].
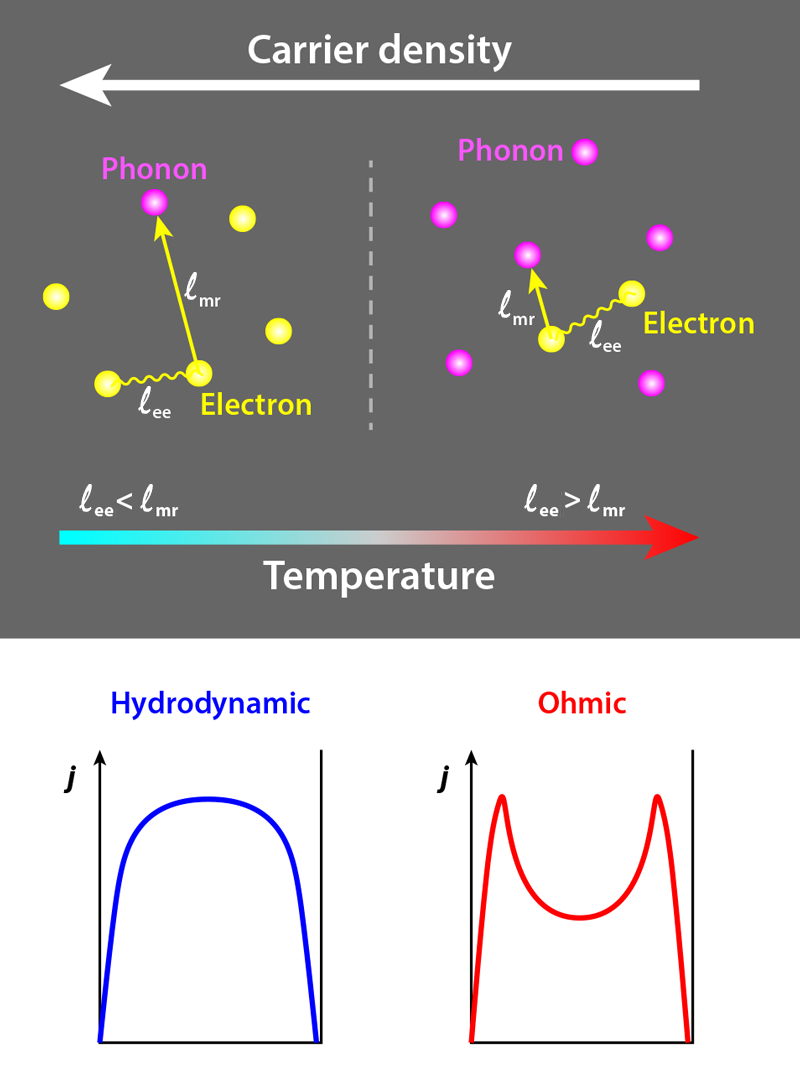
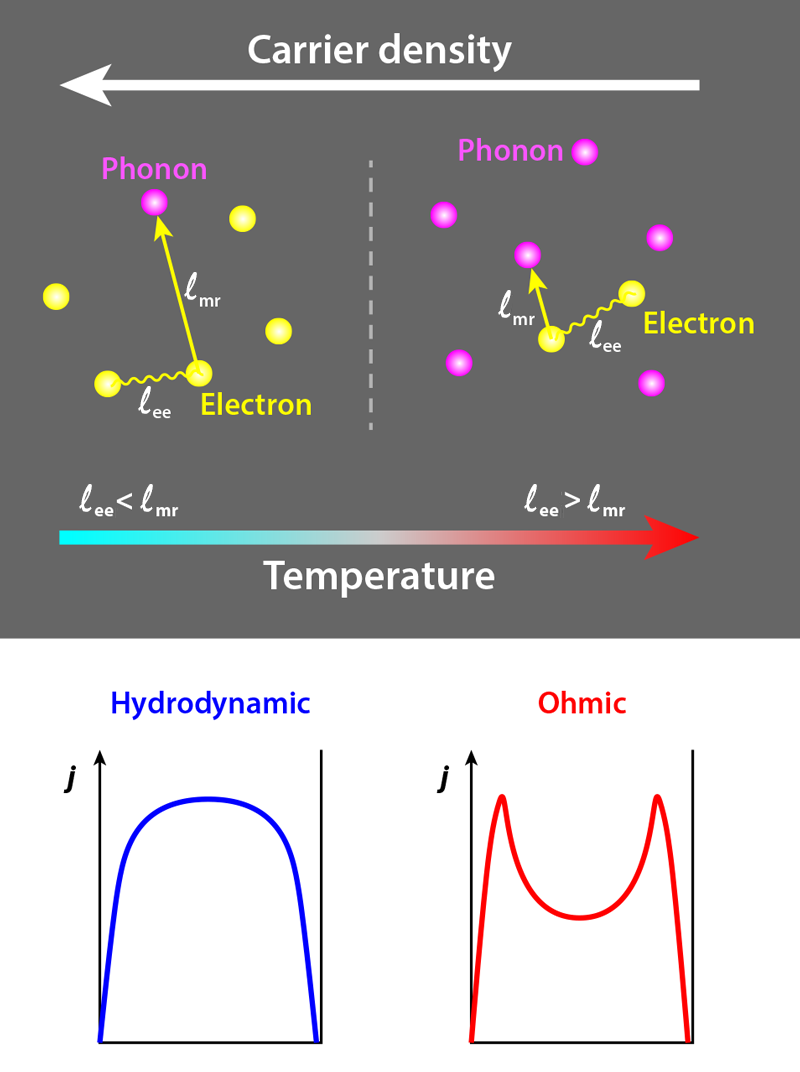
Reaching the hydrodynamic regime poses stringent material requirements connected to the three length scales at play: the size of the sample (W), the average length traveled by electrons between collisions with defects and phonons (the mean free path, ℓmr), and the length traveled by electrons between collisions with each other (the electron-electron scattering length, ℓee). For electron-electron interaction to be dominant, ℓee needs to be smaller than the other two. The conditions to observe such a phenomenon have thus only been realized in high-purity, low-dimensional electron systems, including wires in 2D (Al,Ga)As heterostructures [3], layered metal PdCoO2 [4], and graphene [5–10].
Graphene is of particular interest for studying the hydrodynamic regime because it lacks lattice defects and has weak electron-phonon coupling, which leads to a small probability of collisions with defects and phonons and thus to a large ℓmr. The material also possesses a linear relation between electron energy and momentum (unlike conventional conductors, where this relation is parabolic). This difference decreases ℓee by reducing the effects of electron-electron collisions and the density of low-energy states that screen mutual electron interactions. Such features have allowed the observation of fluid behavior in graphene, associated with a range of exotic phenomena, including a negative local electrical resistance [5], the breakdown of the Wiedemann-Franz law that relates thermal and electrical conductivity [6], the emergence of distinct current-carrying modes that depend on charge density [7], and unusual Hall effects that are manifestations of viscous electron behavior [8, 9].
In most of these studies, however, the detection of the viscous electron flow is indirect, relying on macroscopic magnetotransport [5, 7] or on thermal conductivity [6] measurements combined with complex lithographic engineering of the electron paths. As a consequence, transport measurements depend on device fabrication details, and establishing the emergence of the viscous regime relies heavily on the theoretical interpretation of the data. The direct visualization of local current patterns indicating viscous electron flow has only been realized recently via scanning single-electron transistor microscopy [8] and via NV center magnetometry [1, 10]—the same approach followed by Jenkins and colleagues. No previous experiment, however, has directly visualized the transition from the ohmic regime to the fluid-like regime.
The detection of viscous flow requires a highly sensitive probe that can pick up the small electric signal generated by local currents or, alternatively, a magnetic signal produced by such currents. The latter has become possible by the progress of diamond-NV-center magnetometry [11], which provides a noninvasive method to sense local magnetic fields with high sensitivity and high spatial resolution over a broad temperature range. Jenkins and colleagues adopted this technique to map out the profile of the current flowing through a narrow constriction etched in a graphene sheet.
By controlling doping and temperature, Jenkins and colleagues were able to tune the relative scales of ℓmr and ℓee and to determine—from the current flow patterns in the vicinity of the constricted area—how the tuning affected the conduction regime. For ℓee>ℓmr, the flow is more homogeneously distributed across the channel, with current components at the constriction boundaries larger than those at the center. For ℓee<ℓmr, the flow gets more localized toward the constriction center. These drastic changes in current distribution are hallmarks of the breakdown of the ohmic behavior and of the onset of viscous flow (Fig. 2).
While a recent study also imaged the viscous regime in long graphene channels using an NV magnetometer [10], the work by Jenkins and colleagues provides the first visualization of the transition to such a regime from an ohmic regime. Compared to this previous work [10], the sample geometry and electron density tuning adopted here reduce the experiment’s sensitivity to boundary scattering effects and electron-hole recombination. This feature allowed the researchers to unambiguously establish that diffusive ohmic transport dominates at room temperature, while viscous transport only kicks in below 200 K as the electron-electron interactions get sufficiently strong—and ℓee sufficiently small. Altogether, these observations provide an elegant and clear demonstration of how this electronic transition can be controlled by making ℓee<ℓmr.
One can anticipate that similar approaches could lead to the observation of more exotic electron flow patterns in graphene—a material in which the viscosity of the electron fluid can be an order of magnitude higher than that of honey [5]—as well as in other materials with strong electron-electron correlations. Many phenomena associated with fluid behavior, including electron whirlpools [5], vortices [12], and turbulence [13], may be explored by placing these materials at extreme conditions (such as under large electric fields or thermal gradients). The ability to tune scattering mechanisms and to visualize local electron flows, as demonstrated by Jenkins and colleagues, holds great promise for deciphering the mechanisms underlying these phenomena and for finding strategies to harness them in practical applications.
References
- A. Jenkins et al., “Imaging the breakdown of ohmic transport in graphene,” Phys. Rev. Lett. 129, 087701 (2022).
- R. N. Gurzhi, “Hydrodynamic effects in solids at low temperature,” Sov. Phys. Usp. 11, 255 (1968).
- M. J. M. de Jong and L. W. Molenkamp, “Hydrodynamic electron flow in high-mobility wires,” Phys. Rev. B 51, 13389 (1995).
- P. J. W. Moll et al., “Evidence for hydrodynamic electron flow in PdCoO2,” Science 351, 1061 (2016).
- D. A. Bandurin et al., “Negative local resistance caused by viscous electron backflow in graphene,” Science 351, 1055 (2016).
- J. Crossno et al., “Observation of the Dirac fluid and the breakdown of the Wiedemann-Franz law in graphene,” Science 351, 1058 (2016).
- P. Gallagher et al., “Quantum-critical conductivity of the Dirac fluid in graphene,” Science 364, 158 (2019).
- A. I. Berdyugin et al., “Measuring Hall viscosity of graphene’s electron fluid,” Science 364, 162 (2019).
- J. A. Sulpizio et al., “Visualizing Poiseuille flow of hydrodynamic electrons,” Nature 576, 75 (2019).
- M. J. H. Ku et al., “Imaging viscous flow of the Dirac fluid in graphene,” Nature 583, 537 (2020).
- F. Casola et al., “Probing condensed matter physics with magnetometry based on nitrogen-vacancy centres in diamond,” Nat. Rev. Mater. 3, 17088 (2018).
- L. Levitov and G. Falkovich, “Electron viscosity, current vortices and negative nonlocal resistance in graphene,” Nature Phys 12, 672 (2016).
- D. Di Sante et al., “Turbulent hydrodynamics in strongly correlated Kagome metals,” Nat. Commun. 11, 3997 (2020).