Experiment Sees Elusive Magnetic-Fluid Instability
What do black holes, forming stars, and a tank of liquid metal in Princeton, New Jersey, have in common? The first two might and the third one definitely does play host to an important process in magnetized-fluid dynamics called magnetorotational instability (MRI). MRI has been well studied theoretically and computationally, and related processes have been seen experimentally [1]. But until now, there has not been an unambiguous laboratory confirmation of its existence. Yin Wang and his colleagues at Princeton University have demonstrated MRI in an ingenious liquid-metal experiment—the culmination of more than 20 years of work [2].
The team’s discovery is significant because MRI has long been suspected of being at the heart of accretion [3]. Accretion, in which material spirals inward in a flattened disk around a black hole or a young star, is a major source of the light coming from those objects. For accretion to occur, the material in the disk must lose its angular momentum. However, angular momentum is conserved: much like the trash we generate in our daily lives, it does not cease to exist when it is not wanted. Instead, angular momentum must be passed from the inner parts of the disk to the outer parts. What drives this angular-momentum transport has long been a mystery.
Although MRI was proposed in the late 1950s [4, 5], it wasn’t until the 1990s that it was identified as a potential mechanism for angular-momentum transport in accretion disks [6]. In the past 30 years, a large body of evidence has suggested that MRI-driven turbulence is likely to play a role in accretion. But until now, all that evidence has been theoretical or computational. Wang and colleagues’ work demonstrates that MRI does exist in nature, with properties predicted by theory.
MRI requires two key ingredients: an electrically conductive fluid whose rotational speed decreases outward and an intermediate-strength magnetic field. Such conditions can be produced in a laboratory experiment by adding a liquid metal to a well-established setup called Taylor-Couette flow. This setup consists of two concentric cylinders rotated at different speeds and separated by a gap filled with fluid—typically water or silicone oil. The stability of this fluid system has been studied extensively since 1923 when the physicist Geoffrey Ingram Taylor combined a pioneering experiment with detailed calculations [7]. Taylor showed that fluids rotating at different rates become unstable when their angular momentum decreases outward and when the flow is fast enough to overcome the fluids’ viscosity.
However, accretion disks are powered by the gravity of their central object and, as a result, their angular momentum does not decrease outward. Therefore, the simple form of instability described by Taylor is not present. Theorists have shown that by adding a magnetic field, an electrically conductive fluid can exhibit MRI, and the requirement for instability changes from decreasing angular momentum to decreasing angular velocity. The latter condition is satisfied in accretion disks. Therefore, given that black holes and young stars are nearly always threaded by magnetic fields, MRI is likely to occur in their disks. There are caveats to this conclusion, mainly in the case of young stars, where the disk temperatures are low enough that it is unclear whether the disks are sufficiently ionized to allow magnetic processes such as MRI to operate.
The Princeton experiment uses a liquid-metal alloy called galistan in a Taylor-Couette setup. Galistan has a viscosity about twice as large as that of fresh water but an electrical resistivity 100 million times smaller. Such low resistivity means that electric currents flowing in the fluid become important to its motion. In this magnetohydrodynamic regime, one of the main parameters governing instabilities is the ratio of viscosity to resistivity.
Although galistan is a much better electrical conductor than water, its resistivity is not zero. When a magnetic field passes through a fluid with zero resistivity, it moves with the fluid. But when the resistivity is not zero, the field can slip through the fluid in a process called diffusion. This process tends to smooth out magnetic-field gradients in the same way that a fluid’s viscosity smooths out velocity gradients. In galistan, field gradients are suppressed about a million times faster than velocity gradients.
To see MRI in a Taylor-Couette setup, a quantity called the magnetic Reynolds number must exceed a factor of a few. This quantity is roughly the ratio of the time it takes the fluid to move around the inner cylinder to the time it would take the fluid’s resistivity to diffuse away a magnetic field. For galistan, the diffusion time is short. Therefore, to trigger MRI, the fluid must move rapidly.
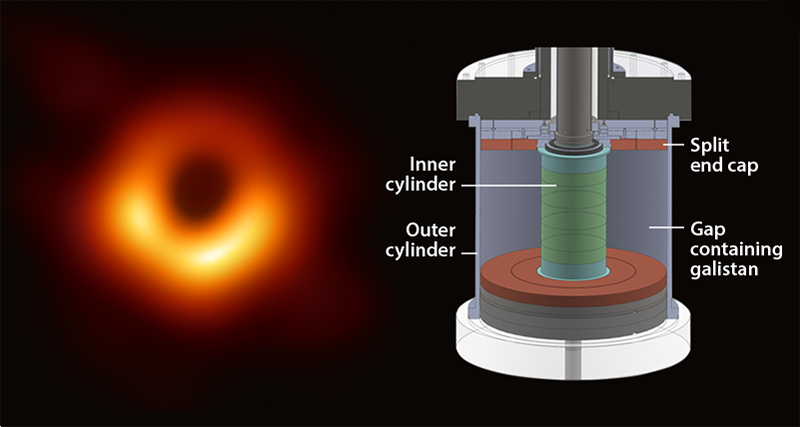
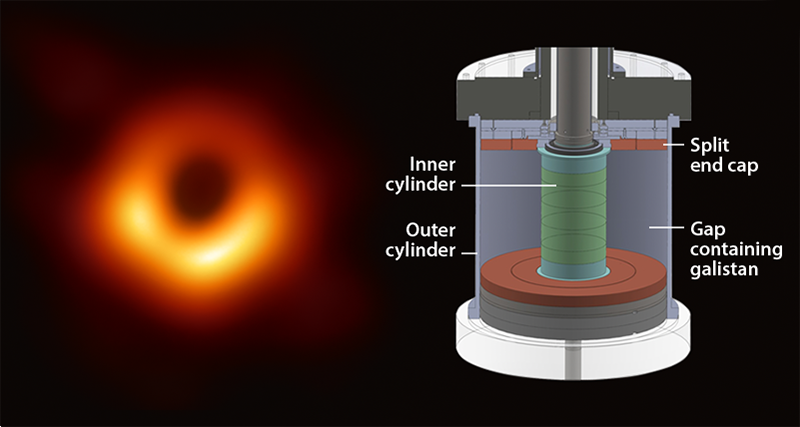
In turn, because the viscosity of galistan is about a million times smaller than its resistivity, there are many other fluid instabilities related to the top and bottom of the setup that could trigger turbulence without MRI. In an accretion disk, there are no lids at the top and bottom, but in an experiment, there are. This seemingly prosaic difference has plagued the laboratory study of MRI for decades. Wang and colleagues developed a clever way around this problem: the end caps are split so that they rotate at speeds intermediate between those of the inner and outer cylinders [8] (Fig. 1). This feature helps to alleviate the secondary flows that plague typical Taylor-Couette experiments, in which the end caps rotate with either the inner or outer cylinder.
The Princeton team made measurements of the radial component of the magnetic field on the inner cylinder, which revealed the predicted hallmarks of MRI. As the magnetic Reynolds number passed the critical threshold, the strength of this radial component began to increase nonlinearly—a key indicator of instability. As further evidence, MRI is predicted to be stabilized by magnetic fields that are stronger or weaker than certain thresholds, and Wang and colleagues saw exactly those behaviors.
The stability theory for MRI is nearly always derived analytically, assuming an infinitely long experiment. Therefore, to more precisely represent their setup, including the end caps, the Princeton team also performed numerical simulations. The experiments and simulations showed instability in the same range of values for the magnetic Reynolds number and for the background field strength. Moreover, the simulations showed angular momentum being transported outward, even when the magnetic Reynolds number was only slightly above the instability threshold.
This work provides a firm experimental basis for MRI, which is a major achievement given that this process has been long thought to be central to accretion but known to exist only through calculations. Although the results provide an estimate of the amount of angular-momentum transport in such experiments, future work will need to precisely measure this key quantity. Importantly, the properties of galistan differ greatly from those of the plasmas that make up accretion disks. Therefore, future experiments will need to study fluids with different viscosities and resistivities to those of galistan to infer the dynamics of these astrophysical objects.
References
- F. Stefani et al., “Experimental evidence for magnetorotational instability in a Taylor-Couette flow under the influence of a helical magnetic field,” Phys. Rev. Lett. 97, 184502 (2006).
- Y. Wang et al., “Observation of axisymmetric standard magnetorotational instability in the laboratory,” Phys. Rev. Lett. 129, 115001 (2022).
- J. Frank et al., Accretion Power in Astrophysics (Cambridge University Press, Cambridge, 2002)[Amazon][WorldCat].
- E. P. Velikhov, “Stability of an ideally conducting liquid flowing between cylinders rotating in a magnetic field,” Sov. Phys. JETP 36, 995 (1959).
- S. Chandrasekhar, “The stability of non-dissipative Couette flow in hydromagnetics,” Proc. Natl. Acad. Sci. U.S.A. 46, 253 (1960).
- S. A. Balbus and J. F. Hawley, “A powerful local shear instability in weakly magnetized disks,” Astrophys. J 376, 214 (1991).
- G. I. Taylor, “Stability of a viscous liquid contained between two rotating cylinders,” Phil. Trans. R. Soc. Lond. A 223, 289 (1923).
- M. J. Burin et al., “Reduction of Ekman circulation within Taylor-Couette flow,” Exp. Fluids 40, 962 (2006).