Measuring Entropy in Active-Matter Systems
A movie of a molecule jostling around in a fluid at equilibrium looks the same when played forward and backward. Such a movie has an “entropy production rate”—the parameter used to quantify this symmetry—of zero; most other movies have a nonzero value, meaning the visualized systems are out of equilibrium. Researchers know how to compute the entropy production rate of simple model systems. But measuring this parameter in experiments is an open problem. Now Sungham Ro of the Technion-Israel Institute of Technology, Buming Guo of New York University, and colleagues have devised a method for making local measurements of the entropy production rate [1]. They demonstrate the technique using simulations and bacteria observations (Fig. 1). The method, which involves comparing forward and time-reversed particle trajectories, could allow researchers to reveal the impact of local entropy production rates on the global dynamics of complex living systems from bacteria to tissues.
Active-matter systems are those composed of energy-consuming agents that exhibit complex collective behavior [2–4]. The classical examples of such agents are birds and fish, which can respectively form flocks that swoop and schools that swirl when they interact in large numbers. Scientists know that these systems break time-reversal symmetry at the single-agent level because of their constant energy consumption [5], and thus active-matter systems have nonzero entropy production rates on the local scale [6].
Scientists also know that active-matter systems break time-reversal symmetry on the global scale, where the agents are observed to collectively organize into patterns—like flocks or schools—whose length scales are much larger than the agents themselves. We don’t, however, know the connection between the global and local breaking of time-reversal symmetry. And simply knowing that the global system has a nonzero entropy production does not tell us much about the system’s behavior. For instance, it tells us how far the system as a whole is from equilibrium, but not where the system is out of equilibrium. Also, we remain in the dark about variations in the system’s thermodynamic properties on intermediate scales. Knowing this information could allow scientists to link the local dynamics of an active-matter system to its global pattern formation, allowing them to use one to predict the other.
To gain this information, scientists have suggested computing local entropy production rates using field-theoretical approaches, but the idea has only been tested for a few specific models [7–9]. Capturing the entropy production rate this way involves collecting “stationary” trajectories (movie frames) from the forward movie and then comparing those frames to ones from the time-reversed movie. This comparison should allow us to quantify regions of the system where nonequilibrium behavior is the most marked. However, accurately quantifying the difference between a stationary trajectory and a time-reversed one is challenging [10]. The work of Ro, Guo, and colleagues takes on this challenge.
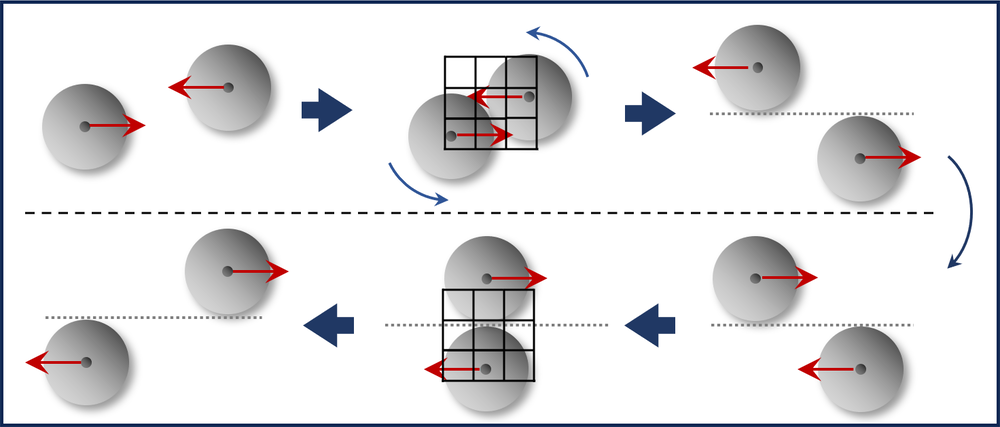
For the study, the team considers a generic active-matter system consisting of self-propelled particles that move randomly in space, performing a “persistent” random walk—a specific kind of random walk where particles move in roughly straight lines. They discretize the system on a grid, associating each point of the grid with an integer number that takes on one of a finite set of values, depending on whether there is a particle at that location (Fig. 2). The value assigned to each point varies in time, giving it a specific time sequence. For the time-reversed movie, the team takes each of these sequences and plays it in reverse: the last value becomes the first. The model takes the sequences in the two movies and compares them using a parameter known as the cross-parsing length, which is used in information theory to quantify the number of shared patterns in two sequences [11]. The more shared patterns in the forward and backward movies, the more symmetrical they are in time and the lower the entropy production rate. Thus, the cross-parsing length is linked to the local entropy production rate.
To benchmark their method, Ro, Guo, and colleagues applied it, for example, to numerical simulations of active Brownian particles undergoing so-called motility induced phase separation—where particles move slower in denser clusters, creating a system with dense and dilute regions—and to experiments with E. coli bacteria that are directed into a specific region via a funnel. For the Brownian particle simulations, they found that the entropy production rate is highest at the boundaries between the dense and dilute regions and lowest in their centers. For the E. coli experiments, they found that the entropy production is highest around the funnels.
The computational protocol introduced by Ro, Guo, and their colleagues will allow researchers to start exploring in more detail the nonequilibrium properties of both natural and fabricated active-matter systems. In principle, that could lead to studies of how nonequilibrium features spread in living systems and how these features connect to the patterns the systems form. For example, it could allow scientists to create nonequilibrium “atlases” for cells and to better understand the collective behavior of living organisms that have no equilibrium counterpart.
References
- S. Ro et al., “Model-free measurement of local entropy production and extractable work in active matter,” Phys. Rev. Lett. 129, 220601 (2022).
- M. C. Marchetti et al., “Hydrodynamics of soft active matter,” Rev. Mod. Phys. 85, 1143 (2013).
- C. Bechinger et al., “Active particles in complex and crowded environments,” Rev. Mod. Phys. 88, 045006 (2016).
- M. J. Bowick et al., “Symmetry, thermodynamics, and topology in active matter,” Phys. Rev. X 12, 010501 (2022).
- E. Fodor et al., “Irreversibility and biased ensembles in active matter: Insights from stochastic thermodynamics,” Annu. Rev. Condens. Matter Phys. 13, 215 (2022).
- E. Fodor et al., “How far from equilibrium is active matter?” Phys. Rev. Lett. 117, 038103 (2016).
- C. Nardini et al., “Entropy production in field theories without time-reversal symmetry: Quantifying the non-equilibrium character of active matter,” Phys. Rev. X 7, 021007 (2017).
- F. Caballero and M. E. Cates, “Stealth entropy production in active field theories near Ising critical points,” Phys. Rev. Lett. 124, 240604 (2020).
- M. Paoluzzi, “Scaling of the entropy production rate in a 𝜙4 model of active matter,” Phys. Rev. E 105, 044139 (2022).
- E. Roldán and J. M. R. Parrondo, “Entropy production and Kullback-Leibler divergence between stationary trajectories of discrete systems,” Phys. Rev. E 85, 031129 (2012).
- J. Ziv and N. Merhav, “A measure of relative entropy between individual sequences with application to universal classification,” IEEE Trans. Inform. Theory 39, 1270 (1993).