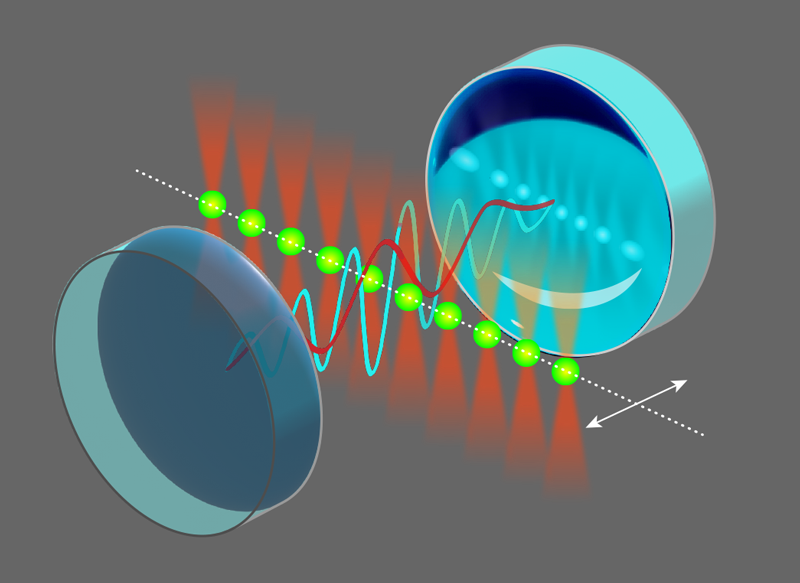
Atom Arrays for Superresolution Imaging
A touchstone for superresolution optical imaging techniques for cold atomic gases is the precision with which they can resolve individual atoms, which are far smaller than the wavelength of the light used for imaging (see Viewpoint: Zooming in on Ultracold Matter). Now, a team based in the US and Germany has turned this problem on its head. Instead of using light to probe atoms, they use atoms to probe an electromagnetic field, taking advantage of the atoms’ tiny size to image the field with high resolution [1]. Using a one-dimensional array of rubidium atoms trapped in optical tweezers, Emma Deist, at the University of California, Berkeley, and colleagues scanned a light field in a cavity with a spatial resolution below the wavelengths of both the cavity field and of the tweezer light. The work may usher in a new generation of metrology and sensing schemes based on individually controlled neutral atoms. It also introduces, for the first time, large arrays of individual atoms into the cavity quantum-electrodynamics (cavity QED) toolbox.
Techniques developed over the last few years have allowed researchers to create large, defect-free atomic arrays that can now approach 1000 atoms in two dimensions [2]. These advances have made atomic arrays a prominent platform for quantum information science, with applications ranging from quantum simulation to quantum computing to precision optical metrology [3]. Deist and colleagues extend the use of atom arrays in the latter category, employing a comparatively modest, one-dimensional array of up to ten atoms to probe the intensity of a standing-wave field inside an optical cavity.
The row of atoms used by the researchers extends along the radial direction of the cavity mode (i.e., perpendicular to the cavity axis). They scan this array along the cavity axis, thereby encompassing the two-dimensional plane defined by the cavity’s radial and axial directions (Fig. 1). The cavity field shifts the resonance frequency of an atomic transition, and, by measuring the rate of the fluorescence induced by a calibrated probe beam, the team determines the intensity of the field at any position in the wave. The result is a beautiful map of the profile of the field, revealing a Gaussian field distribution with a radius of 26𝜇m, consistent with predictions based on the cavity geometry and on the cavity field’s wavelength of 1560 nm.
Since the tweezer array localizing the atoms is positioned with electrically actuated adaptive optical elements, the positions of the atoms can be controlled with a precision much greater than the optical wavelength of the light used to generate the tweezers and detect the atoms. For example, the acousto-optic deflector (AOD) used to generate the tweezers provides a mapping between the radio frequency in the AOD and the position of the tweezer in the focal plane [3], with a typical conversion of ∼10𝜇m∕MHz. Thus, radio-frequency precision at the kHz level can, in principle, position a tweezer with a spatial precision of 10nm despite the size of the tweezer itself being ∼1𝜇m.
Deist and colleagues employ this capability to probe the cavity field on length scales shorter than the field’s 1560-nm wavelength and the 780-nm wavelength of the fluoresced light used to perform the measurement. The ultimate limit on the spatial precision of their approach is set by the accuracy with which the atoms can be localized within their respective tweezers. For atoms cooled to the motional ground state of their optical tweezers, the atomic wave function can be as small as ∼10nm (assuming a trap depth of ∼1mK and a tweezer 1∕e2 waist radius of ∼500nm). In their experiment, Deist and colleagues have slightly hotter atoms which, when combined with other technical factors, limit the spatial resolution to 300nm. However, further cooling [3] and other technical upgrades are readily available, offering significant improvements to the possible resolution.
The researchers also introduce a second field into the cavity with a wavelength of 781 nm—slightly larger than half that of the first field. This short-wavelength field induces forces sufficiently large to displace the atoms in the tweezers, thereby distorting the measurements of the long-wavelength cavity field made using the method described above. In this way, the team uses the atom array as a field-sensitive force sensor—an atomic-force supermicroscope.
The techniques demonstrated by Deist and colleagues could be helpful for diagnosing optical fields in myriad applications—not only in optical cavity systems such as that used in their experiment but also in optical lattice systems, where, for example, the investigation of Hubbard models requires ever-improving control of optical potentials [4]. Beyond optical metrology, marrying a scalable array of single atoms to an optical cavity with strong atom-photon coupling is an enabling breakthrough for quantum information technologies. Systems with atoms coupled to optical cavities—described by cavity QED—offer the ability to entangle atomic spins with photons. Such entanglement could then be used to generate atom-atom entanglement within the cavity, perform nondemolition measurements of atomic spins, and generate remote entanglement between separated systems via a photonic quantum bus—essential operations for quantum computing and communication hardware built on this platform. Cavity QED with single atoms or with atomic ensembles has been studied for the past few decades, but only recently has it been applied to a pair of individual atoms [5] and to an ordered array of atomic ensembles [6]. Deist and colleagues are the first to demonstrate a cavity QED system combined with a scalable array of individual atoms.
Another field of application involves schemes with highly excited “Rydberg” states [7], which have recently become the dominant approach to entanglement of neutral atoms. Entanglement “fidelities” using this approach now exceed 0.99 [8]—beyond what can readily be achieved using photon-mediated interactions in a cavity [5]. However, as Rydberg atoms interact with each other via their electric dipole moments, Rydberg interactions are inherently short range, which complicates the development of many-body entangled states such as logically encoded qubits. Photon-mediated interactions in optical cavities could solve this problem [9, 10] because they act on an infinitely long range. Unfortunately, stray electric fields generated by the dielectric surfaces of the mirrors cause a transient Stark shift in the Rydberg states that adversely affects the ability to reliably perform Rydberg-based entangling operations. Deist and colleagues avoid this problem by employing a near-concentric cavity with a large (1 cm) mirror spacing. Near-concentric cavities provide small mode volumes (and thus strong atom-photon coupling) even with such large mirror separation. Since the mirrors in this setup are sufficiently far away from the atoms, the marriage of cavity QED with strong coupling and Rydberg atom arrays is made possible for the first time.
References
- E. Deist et al., “Superresolution microscopy of optical fields using tweezer-trapped single atoms,” Phys. Rev. Lett. 128, 083201 (2022).
- S. Ebadi et al., “Quantum phases of matter on a 256-atom programmable quantum simulator,” Nature 595, 227 (2021).
- A. M. Kaufman and K.-K. Ni, “Quantum science with optical tweezer arrays of ultracold atoms and molecules,” Nat. Phys. 17, 1324 (2021).
- P. Zupancic et al., “Ultra-precise holographic beam shaping for microscopic quantum control,” Opt. Express 24, 13881 (2016).
- S. Welte et al., “Photon-mediated quantum gate between two neutral atoms in an optical cavity,” Phys. Rev. X 8, 011018 (2018).
- Avikar Periwal et al., “Programmable interactions and emergent geometry in an array of atom clouds,” Nature 600, 630 (2021).
- M. Saffman et al., “Quantum information with Rydberg atoms,” Rev. Mod. Phys. 82, 2313 (2010).
- I. S. Madjarov et al., “High-fidelity entanglement and detection of alkaline-earth Rydberg atoms,” Nat. Phys. 16, 857 (2020).
- W. Huie et al., “Multiplexed telecommunication-band quantum networking with atom arrays in optical cavities,” Phys. Rev. Res. 3, 043154 (2021).
- J. Ramette et al., “Any-to-any connected cavity-mediated architecture for quantum computing with trapped ions or Rydberg arrays,” arXiv:2109.11551 .