Two Spins Take the Quantum Bus

Guido Burkard

Viewpoint

Two Spins Take the Quantum Bus

Department of Physics, University of Konstanz, Konstanz, Germany

May 2, 2022• Physics 15, 65

Coupling between remote spins on a chip via virtual photons exchanged through a superconducting resonator could lead to gate operations between distant spin qubits.

Figure caption — **Figure 1:** Two qubits coupled to the same microwave resonator can be coupled via the exchange of virtual photons.

Both superconducting and semiconducting systems are the focus of intense ongoing research and development as platforms for quantum-information hardware. At the same time, superconducting-semiconducting hybrid quantum systems are attracting considerable attention, since they can combine interesting physical properties of both material classes and can sometimes exhibit entirely new properties. Now, a group led by Lieven Vandersypen at Delft University of Technology in the Netherlands has succeeded in coherently coupling two electron spins in separate semiconductor nanostructures via the exchange of virtual photons through a superconducting microwave resonator [1]. Their demonstration marks a milestone in semiconductor spin-qubit research and offers new possibilities for spin-based quantum computing.

Nearly a century ago, physicists found that the electron comes with an intrinsic quantized angular momentum. This electron spin lends itself to quantum computing, as its two states, up and down, can serve as the “0” and “1” of a qubit [2]. While the electron charge reacts to both electric and magnetic fields, the spin only couples to the magnetic field. For spin qubits, this is a good thing because in solid-state devices the main source of deleterious noise is electric. This spin advantage is particularly true for isotopically purified $^{28} Si$ —the material used by the Delft team [1]—where magnetic noise is suppressed to an exceedingly low level.

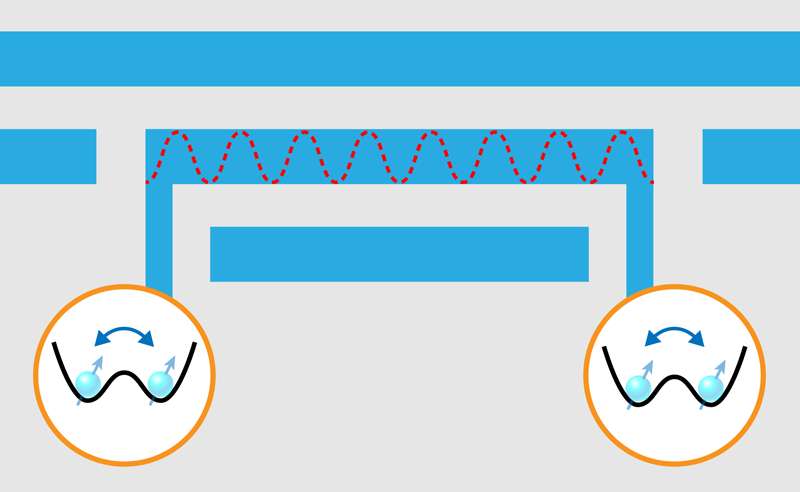
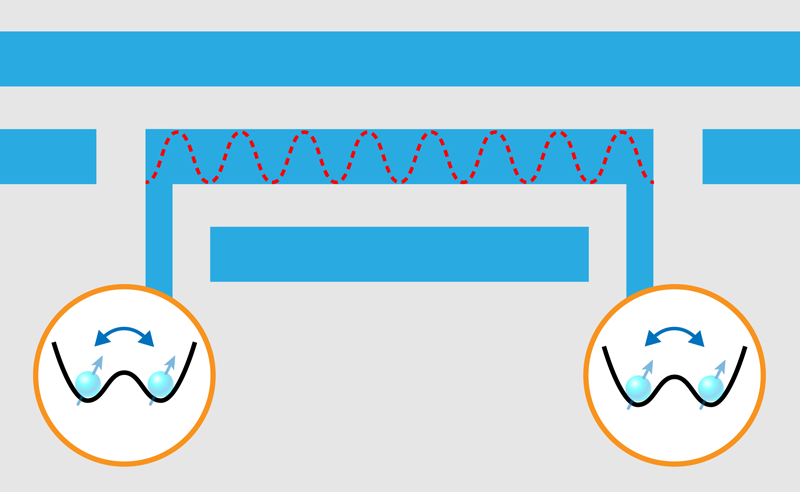
However, the noninteraction of spin with electric fields can pose a problem when one needs a long-range interaction, or “quantum bus,” for coupling two distant qubits (Fig. 1). In the superconducting world, this problem was solved 15 years ago by using a superconducting microwave resonator as quantum bus between two distant superconducting qubits on a processor chip [3]. Superconducting qubits are based on electric charge, which couples directly to the electric field created by a cavity photon. Microwave photons are typically used for on-chip communication because their frequency matches the transition frequency of both superconductor and semiconductor qubits. However, for spin qubits, photon-mediated interactions are more difficult to realize, as the coupling between electron spins and the magnetic field of a cavity photon is much weaker. How, then, can long-range interactions between spin qubits be achieved while protecting those qubits from electric fluctuations? This problem can be solved if the coupling of the spin to the electric field can be effectively switched on and off.

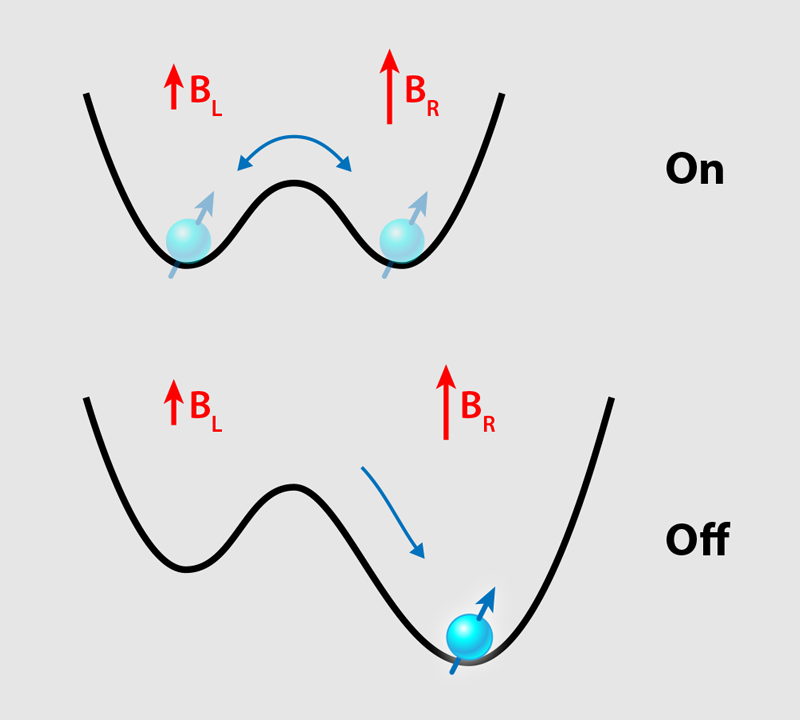
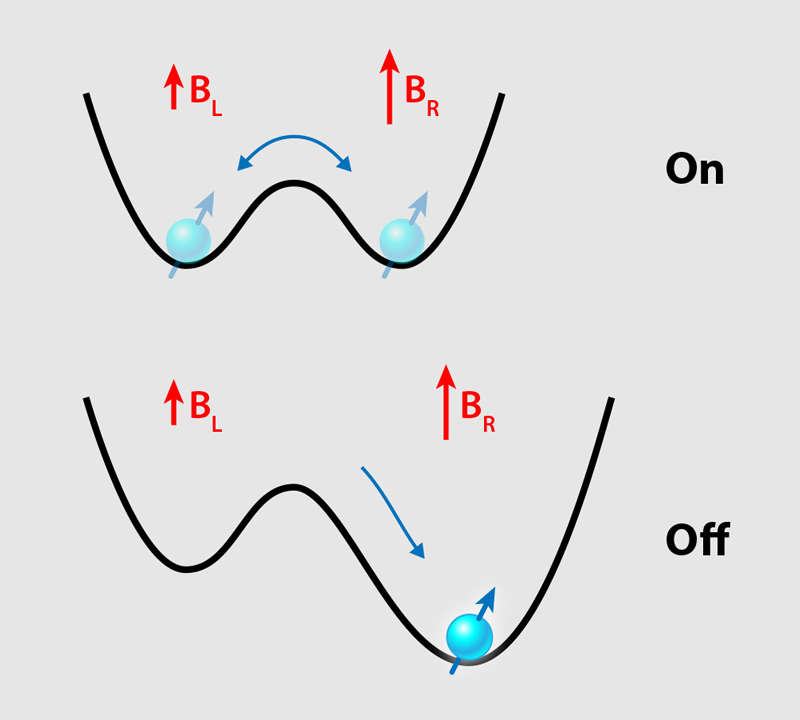
The new work by the Delft group [1] makes use of an effective method to control the spin-photon coupling. The method uses a trick called a flopping-mode qubit, in which a single electron behaves as both a spin qubit and a charge qubit [4]. The charge qubit is associated with the electron’s position in a double-well potential, with the left side of the potential chosen to be the “0” state and the right side chosen for the “1” state. The coupling of the spin and charge qubits relies on the presence of a magnetic-field gradient produced by an on-chip micromagnet [5], which causes the spin qubit to experience a different magnetic field when the electron moves between the two sides of the potential.

The spin-charge-coupling mechanism can be switched on by making the double-well potential symmetric, thus allowing the electron to explore both wells (Fig. 2). In this condition, the system is maximally sensitive to the electric field of a cavity photon. The coupling is switched off by making the double well very asymmetric, such that the electron falls into the lower potential well where it remains immobile and thus insensitive to electric fields.

This technique enabled a series of breakthrough experiments, published in 2018 [6–8], in which strong spin-photon coupling was first observed between the electronic spin in a semiconductor quantum-dot structure and the photons in a superconducting microwave resonator. The achievement of the strong coupling regime of cavity quantum electrodynamics is significant and means that the spin-photon coupling $g_{s}$ exceeds the spin and cavity decay rates. This allows for the coherent exchange of quantum information between the spin and the photon and represents the first necessary step toward the exchange of quantum information between two spins via the cavity photons (Fig. 1). Using this technique, researchers observed the first signatures of cavity-mediated interactions between two remote spin qubits [9]. In this case, the microwave cavity mode was on resonance, which means the cavity-photon and spin-qubit energies coincided.

Building on this earlier work, the Delft team designed an experiment with two silicon-based quantum dots connected to the ends of a 250- $𝜇$ m-long superconducting microwave cavity [1]. The researchers tuned the energy splitting between the up and down states for each of the two qubits using a combination of on-chip micromagnets and a homogeneous external magnetic field [9]. What sets the new work apart is that it operates in the so-called strong dispersive regime, where the cavity photon and qubit frequencies differ by an amount $Δ_{s}$ that is much greater than the spin-photon coupling $g_{s}$ and where the spin-photon interaction creates an energy shift in the cavity frequency exceeding the spin and cavity decay rates. As a result of these energy offsets, interactions between the two qubits are mediated by virtual photons—in other words, photons that have a very small probability of being detected in the cavity. Coupling spins via virtual photons is the preferred method because it is much less affected by the occasional loss of cavity photons. Previous work has utilized the strong dispersive regime for realizing superconducting two-qubit gates [3], and the regime has been targeted in models of future semiconductor spin-based two-qubit gates [10].

To achieve strong dispersive coupling, the Delft team used a high-impedance superconducting resonator to strengthen the charge-photon coupling and, as a result, the spin-photon coupling $g_{s}$ [1]. Having reached the strong dispersive regime, the Delft team realized two hallmark demonstrations. First, they observed the nonlocal spin-spin exchange mediated by virtual cavity photons. This demonstration required the exchange coupling $J \approx g_{s}^{2} ∕ Δ_{s}$ to be larger than the decay rates and involved turning on the coupling of both spins to the common photon mode simultaneously. The team then tuned the qubit frequencies by rotating the external magnetic field and monitored the states with a microwave pump-probe detection scheme. As the two qubit frequencies became equal, the qubit states hybridized and produced a measurable splitting of $2 J$ in the energy of the spin states. The second hallmark demonstration was the observation of a photon-number-dependent shift of the qubit energy, which will allow for photon-state measurement and high-fidelity qubit readout by measuring a qubit-state-dependent shift of the photon frequency.

With these new results, spin qubits are catching up with superconducting qubits as a practical quantum-computing platform. What still need to be demonstrated are quantum bits that can be made to work in the time domain by switching the coupling on and off. But the newly achieved long-range connectivity—combined with the potential for high-fidelity readout, the long coherence times, and the small footprint on the chip—puts semiconductor spin qubits in an ideal position to realize large-scale and high-fidelity quantum processors.

References

P. Harvey-Collard et al., “Coherent spin-spin coupling mediated by virtual microwave photons,” Phys. Rev. X 12, 021026 (2022).
D. Loss and D. P. DiVincenzo, “Quantum computation with quantum dots,” Phys. Rev. A 57, 120 (1998).
J. Majer et al., “Coupling superconducting qubits via a cavity bus,” Nature 449, 443 (2007).
M. Benito et al., “Input-output theory for spin-photon coupling in Si double quantum dots,” Phys. Rev. B 96, 235434 (2017).
M. Pioro-Ladrière et al., “Electrically driven single-electron spin resonance in a slanting Zeeman field,” Nature 4, 776 (2008).
X. Mi et al., “A coherent spin–photon interface in silicon,” Nature 555, 599 (2018).
N. Samkharadze et al., “Strong spin-photon coupling in silicon,” Science 359, 1123 (2018).
A. J. Landig et al., “Coherent spin–photon coupling using a resonant exchange qubit,” Nature 560, 179 (2018).
F. Borjans et al., “Resonant microwave-mediated interactions between distant electron spins,” Nature 577, 195 (2019).
Ada Warren et al., “Long-distance entangling gates between quantum dot spins mediated by a superconducting resonator,” Phys. Rev. B 100, 161303 (2019); M. Benito et al., “Optimized cavity-mediated dispersive two-qubit gates between spin qubits,” 100, 081412 (2019).

About the Author

Guido Burkard studied physics at the Swiss Federal Institute of Technology (ETH) in Zurich and received his Ph.D. from the University of Basel in Switzerland. Since 2008, he has been a full professor at the University of Konstanz, Germany. He previously held a faculty position at RWTH Aachen University, Germany, and was SNF assistant professor at the University of Basel, after a postdoctoral appointment with the IBM Thomas J. Watson Research Center at Yorktown Heights, New York. His research interests encompass condensed-matter theory and quantum information, with special focus on the theory of solid-state qubits and hybrid quantum systems. In 2019 he was recognized as an Outstanding Referee by the American Physical Society