Memories Become Chaotic before They Are Forgotten
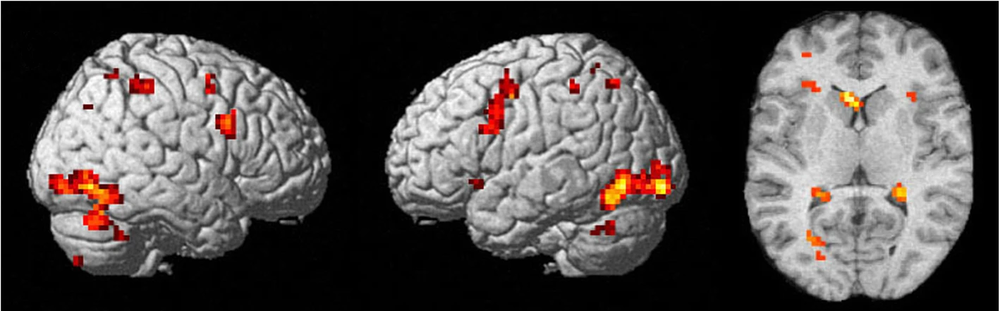
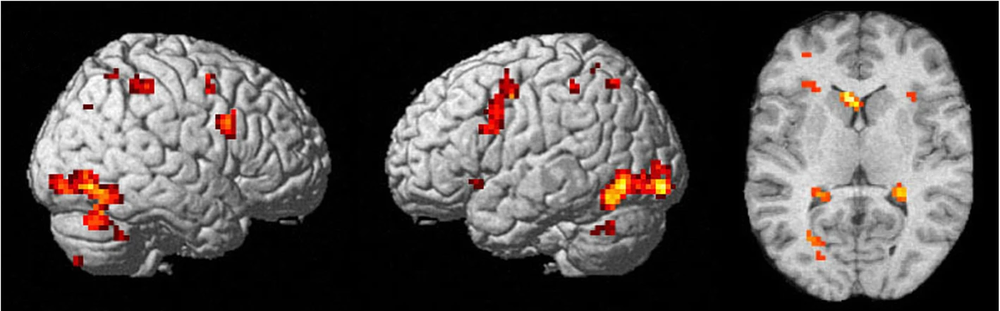
Theoretical constructs called attractor networks provide a model for memory in the brain. A new study of such networks traces the route by which memories are stored and ultimately forgotten [1]. The mathematical model and simulations show that, as they age, memories recorded in patterns of neural activity become chaotic—impossible to predict—before disintegrating into random noise. Whether this behavior occurs in real brains remains to be seen, but the researchers propose looking for it by monitoring how neural activity changes over time in memory-retrieval tasks.
Memories in both artificial and biological neural networks are stored and retrieved as patterns in the way signals are passed among many nodes (neurons) in a network. In an artificial neural network, each node’s output value at any time is determined by the inputs it receives from the other nodes to which it’s connected. Analogously, the likelihood of a biological neuron “firing” (sending out an electrical pulse), as well as the frequency of firing, depends on its inputs. In another analogy with neurons, the links between nodes, which represent synapses, have “weights” that can amplify or reduce the signals they transmit. The weight of a given link is determined by the degree of synchronization of the two nodes that it connects and may be altered as new memories are stored.
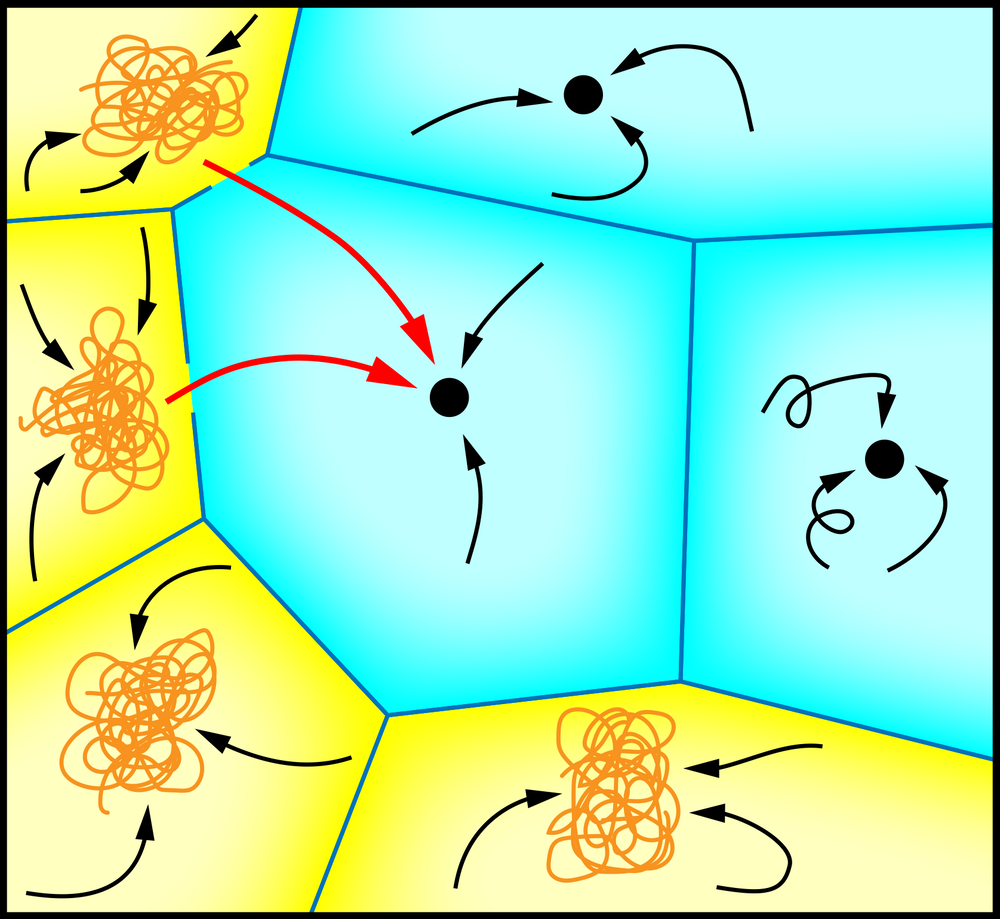
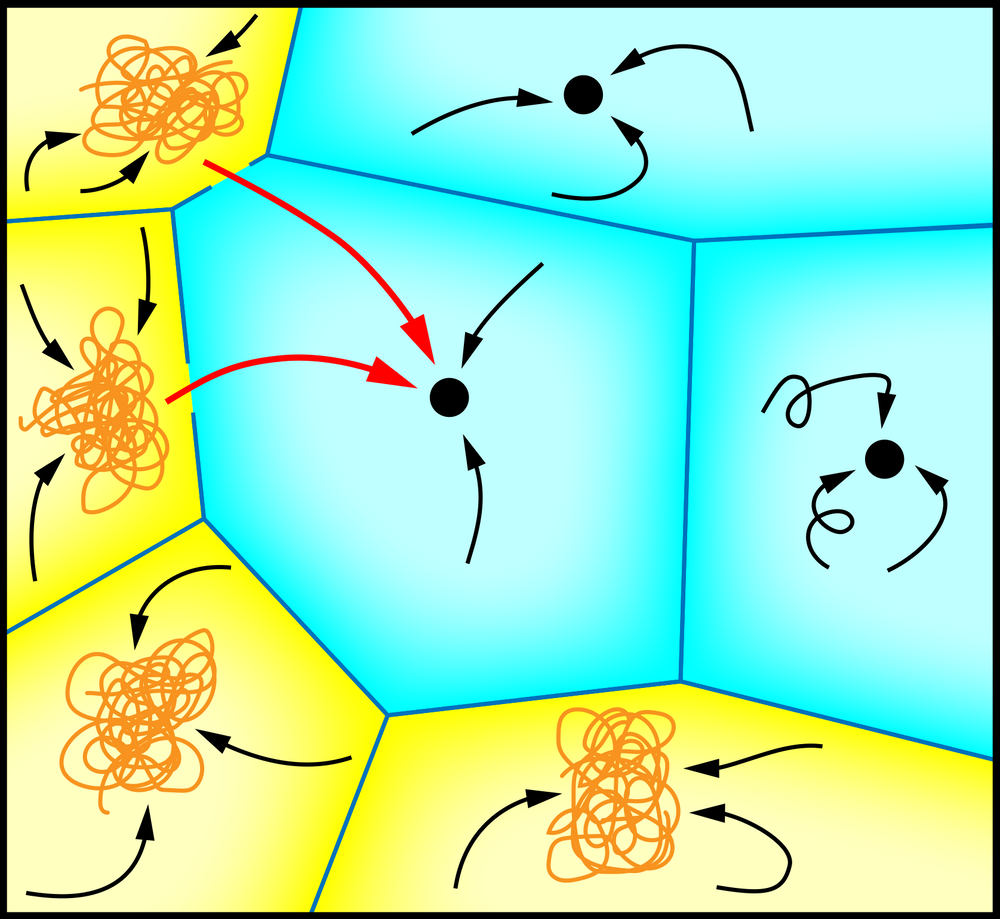
In attractor networks, the signals exchanged between nodes have values taken to represent the firing rates of real neurons; the firing rates become the inputs that determine the responses of the receiving neurons. There is a constant, shifting flux of such signals traveling through the network. To imprint a “memory” in the network, researchers can take a long binary number (representing the remembered item), assign one of its digits to each node, and then observe how the network’s activity evolves as the weights readjust. The signals passing between nodes eventually settle into a repeating pattern, called an attractor state, which encodes the memory.
The memory can be retrieved if a new binary number with a simple mathematical relation to the one that created the memory is applied to the nodes, which may shift the activity of the network into the corresponding attractor state. Typically, an attractor network can hold many distinct memories, each of which corresponds to a different attractor state. The activity of the network then wanders between all of these states.
Previous studies of biological neural networks have shown that their network activity is noisier (more random) than might be expected from a network imprinted only with well-defined, stable attractor states [2–4]. In addition, research on attractor networks has suggested that they can undergo “catastrophic forgetting”: if too many memory states are imprinted, none can be retrieved at all [5].
Neuroscientist Ulises Pereira-Obilinovic of New York University and O’Higgins University in Chile and his colleagues investigated how this behavior changes if the memory states are not permanent. The researchers’ rule for updating weights causes the weights established when a memory is imprinted to gradually fade as subsequent memories are added. Their simulations produce two types of memory states. As memories are sequentially imprinted, the newest ones correspond to “fixed-point” attractors with well-defined and persistent patterns, much like the orbits of the planets around the Sun. But as the memory states age and fade, they transform into the second type, chaotic attractors, whose activity never precisely repeats, making them more like weather patterns. A transition from fixed-point to chaotic dynamics in neural networks has been reported before [6, 7] but not in networks that could both learn and forget.
As more memories are learned by the network, the apparent randomness in chaotic attractors increases until the oldest attractor state dissipates into mere noise. At this stage the memory can no longer be retrieved: it is completely “forgotten.” So the results imply that, in this network, “forgetting” involves first a switch from regular to chaotic activity (which makes the retrieved memory less faithful to the original), followed by dissolution into noise, with a characteristic decay time. There is also no catastrophic forgetting because older memories fade automatically in this model, and so there is no possibility of overload.
If this process of “forgetting” applies to the brain, the researchers predict that the fluctuations in neuron firing times should be greater when older memories are being retrieved because these will be stored as chaotic and increasingly noisy states. The researchers say that this idea should be testable by recording neural activity during memory tasks with increasing delays between the input and the person’s or animal’s response to recalling the memory.
Neuroscientist Tilo Schwalger of the Technical University of Berlin believes that the predictions should indeed be testable and that the findings might turn out to be applicable to neural networks in animals. Neuroscientist Francesca Mastrogiuseppe of the biosciences organization Champalimaud Research in Portugal agrees, adding that the research “sits at the intersection between two major lines of work in theoretical neuroscience: one related to memory; the other related to irregular neural activity in the brain.” The new results show that the two phenomena might be linked, she says.
–Philip Ball
Philip Ball is a freelance science writer in London. His latest book is How Life Works (Picador, 2024).
References
- U. Pereira-Obilinovic et al., “Forgetting leads to chaos in attractor networks,” Phys. Rev. X 13, 011009 (2023).
- F. Barbieri and N. Brunel, “Irregular persistent activity induced by synaptic excitatory feedback,” Front. Comput. Neurosci. 1 (2007).
- G. Mongillo et al., “Synaptic theory of working memory,” Science 319, 1543 (2008).
- M. Lundqvist et al., “Bistable, irregular firing and population oscillations in a modular attractor memory network,” PLoS Comput. Biol. 6, e1000803 (2010).
- J. P. Nadal et al., “Networks of formal neurons and memory palimpsests,” Europhys. Lett. 1, 535 (1986).
- B. Tirozzi and M. Tsodyks, “Chaos in highly diluted neural networks,” Europhys. Lett. 14, 727 (1991).
- U. Pereira and N. Brunel, “Attractor dynamics in networks with learning rules inferred from in vivo data,” Neuron 99, 227 (2018).