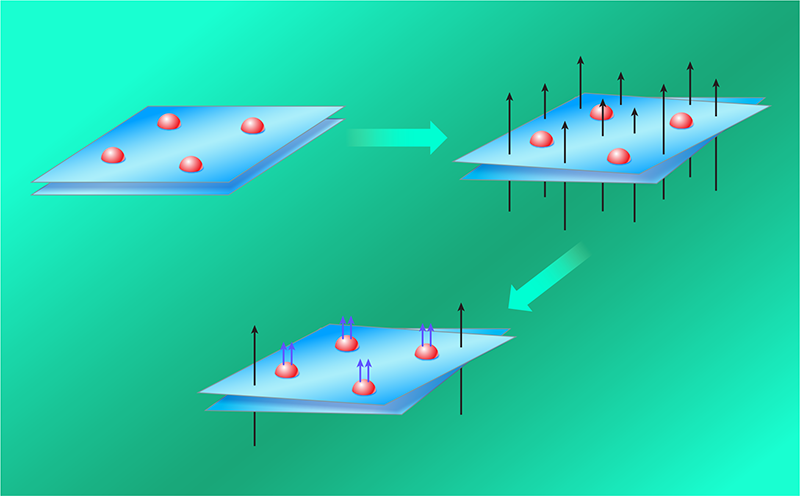
In a Twist, Composite Fermions Form and Flow without a Magnetic Field
Materials scientists have engineered systems in the laboratory that yield exotic particles not seen in nature. In particular, when electrons are confined to two dimensions, cooled to near absolute zero, and exposed to a strong magnetic field, they capture part of this field and turn into weakly interacting particles called composite fermions (CFs). CFs display striking phenomena such as the fractional quantum Hall effect (FQHE). (See [1] for reviews of CFs, the FQHE, and other early developments.) Recently, experiments showed that a particular twisted semiconductor bilayer exhibits CFs and the FQHE without an applied magnetic field [2–5] (Fig. 1). Now, based on a theoretical analysis of these experiments, two research teams predict that this twisted bilayer should also realize a state called a CF Fermi liquid [6, 7]. The ability to create a CF Fermi liquid at zero magnetic field would enable a comprehensive exploration of this peculiar state, which provides a new paradigm for metallic behavior and can serve as a parent to other interesting states.
The path to these discoveries runs through several previous breakthroughs. In the early 1980s, physicists were drawn to the system of a two-dimensional electron gas in a strong magnetic field by the unexpected discoveries of the integer quantum Hall effect (IQHE) and of the FQHE in this system. The IQHE refers to the observation of plateaus where a charge-transport parameter known as the Hall resistance RH is precisely quantized at values given by RH = h/(ne2). Here, h is Planck’s constant, e is the electron’s charge, and n is an integer. This quantization is a property of n filled Landau levels, which are electronic bands of constant kinetic energy created by the magnetic field. Materials with filled Landau levels display the IQHE, instead of the insulating behavior expected from filled bands, because Landau levels are topological—that is, they have a nonzero integer value of what mathematicians call the Chern number C [8]. Any topological band, whether produced by a magnetic field or by some other means, will exhibit RH = h/(Ce2) when fully occupied by electrons.
The FQHE refers to the existence of a plateau at RH = h/(fe2), where f is a fraction. Such a plateau occurs when electrons fill approximately this fraction of a Landau level. The number of observed fractions has swelled from one (f = 1/3) in 1982 to about 100 today. In contrast to the IQHE, the FQHE is caused by strong electron correlations resulting from the repulsive Coulomb interaction. Essentially, to avoid one another as efficiently as possible, electrons capture an even number of magnetic-field quanta and transform into CFs. The CFs “see” only the uncaptured field, and their IQHE manifests as the FQHE of electrons at sequences of odd-denominator filling fractions.
The strategy for producing CFs and the FQHE at zero magnetic field is, then, to identify a material that has an electronic band mimicking a Landau level. This band must be topological (have a nonzero Chern number), be of roughly constant kinetic energy, and generate a pseudomagnetic field that is as uniform as possible. Building on earlier works [9], researchers predicted that these desired properties would be exhibited by certain bands in a MoTe2 semiconductor bilayer whose layers are slightly twisted relative to each other [10]. Indeed, recent optical [2, 3] and transport [4, 5] experiments showed that this system displays the FQHE at the odd-denominator filling fractions of f = 2/3 and f = 3/5 without a magnetic field.
Now Hart Goldman and colleagues at the Massachusetts Institute of Technology [6] and Junkai Dong and colleagues at Harvard University [7] present comprehensive numerical and analytical studies of the interacting electrons that partially populate one of the aforementioned topological bands in twisted bilayer MoTe2. The two teams’ results strongly suggest that CFs also form at the even-denominator filling fractions of f = 1/2 and f = 3/4 without any external magnetic field. At these fractions, CFs would see no pseudomagnetic field and are predicted to condense into a CF Fermi liquid—a strongly correlated metallic state that is fundamentally distinct from the ordinary, weakly correlated, electron Fermi liquid found in metals.
The recent transport experiments showed a gapless state—one that lacks an energy gap between its ground and excited levels—at f = 1/2 [4]. That observation is consistent with the behavior of a CF Fermi liquid but does not prove its existence. Goldman and Dong and their colleagues propose several ways to experimentally distinguish a CF Fermi liquid from an ordinary electron Fermi liquid. These methods include observing oscillations in the system’s electronic properties as one varies either the concentration of charge carriers or the strength of an applied magnetic field.
The observation of the FQHE and the prediction of a CF Fermi liquid at zero magnetic field will undoubtedly spark further study that promises to deliver the FQHE at additional filling fractions and other exciting discoveries. The topological bands of twisted semiconductor bilayers are not identical to Landau levels and might produce phenomena beyond those seen with Landau levels. Moreover, the absence of a magnetic field will facilitate new experiments—such as angle-resolved photoemission spectroscopy of these CF states, studies of topological phase transitions induced by applying a perpendicular electric field, probes of the coupling of CF states to superconductivity, and investigations of charge transport across the junction between a CF Fermi liquid and an ordinary electron Fermi liquid. Finally, the CF Fermi liquid could be a precursor to an unusual CF superconductor harboring particles known as non-Abelian anyons that have been envisioned as building blocks of future fault-tolerant quantum computers.
References
- B. I. Halperin and J. K. Jain, “Fractional Quantum Hall Effects: New Developments,” (World Scientific, Singapore, 2020)[Amazon][WorldCat].
- J. Cai et al., “Signatures of fractional quantum anomalous Hall states in twisted MoTe2,” Nature (2023).
- Y. Zeng et al., “Thermodynamic evidence of fractional Chern insulator in moiré MoTe2,” Nature (2023).
- H. Park et al., “Observation of fractionally quantized anomalous Hall effect,” Nature (2023).
- F. Xu et al., “Observation of integer and fractional quantum anomalous Hall effects in twisted bilayer MoTe2,” Phys. Rev. X 13, 031037 (2023).
- H. Goldman et al., “Zero-field composite Fermi liquid in twisted semiconductor bilayers,” Phys. Rev. Lett. 131, 136501 (2023).
- J. Dong et al., “Composite Fermi liquid at zero magnetic field in twisted MoTe2,” Phys. Rev. Lett. 131, 136502 (2023).
- D. J. Thouless et al., “Quantized Hall conductance in a two-dimensional periodic potential,” Phys. Rev. Lett. 49, 405 (1982).
- F. D. M. Haldane, “Model for a quantum Hall effect without Landau levels: Condensed-matter realization of the ‘parity anomaly’,” Phys. Rev. Lett. 61, 2015 (1988); C. L. Kane and E. J. Mele, “Z2 topological order and the quantum spin Hall effect,” 95, 146802 (2005); R. Bistritzer and A. H. MacDonald, “Transport between twisted graphene layers,” Phys. Rev. B 81, 245412 (2010).
- F. Wu et al., “Topological insulators in twisted transition metal dichalcogenide homobilayers,” Phys. Rev. Lett. 122, 086402 (2019).