Two Black Holes Masquerading as One
Black holes are astonishing objects that can pack the mass of Earth into a space the size of a pea. A remarkable attribute is their stunning simplicity, which is encapsulated in the celebrated uniqueness theorems [1]. Briefly stated, these theorems say that there is only one solution to Einstein’s equations of general relativity for a fully collapsed (nonevolving) system having fixed mass and angular momentum [2]. The implication is that all black holes that have settled down to equilibrium with the same mass and rotation are precisely the same: their entire behavior described by a single equation—the so-called Kerr solution—filling only a few lines of paper!
But there is a catch. The uniqueness theorems make a number of assumptions, the key one being that the space around the black hole is “empty”—in other words, there is no energy that might influence the black hole. Such energy can arise from fields, for example, those of the standard model, or from a “cosmological constant,” which is a form of dark energy that might be behind the accelerated expansion of our Universe today. In a fascinating study, Óscar Dias from the University of Southampton, UK, and colleagues demonstrate that uniqueness is violated in the presence of a positive cosmological constant [3]. Specifically, they show that a pair of black holes whose mutual attraction is balanced by the cosmic expansion would look the same to a distant observer as a single isolated black hole. The results may lead to a rethinking of how simple black holes really are.
The question of black-hole uniqueness has long been an issue. Interpreting gravitational waveforms from merging binary systems is made possible because of the simplicity of the individual black holes involved in the merger. Uniqueness is also the basis of Stephen Hawking’s information loss paradox [4]. When matter collapses to form a black hole, all the complex information about what fell in is lost since the resulting black hole is defined only by its total mass and angular momentum.
Given the importance of uniqueness for both observations and theory, a relevant question is how generally it holds. This is simplest to address for “static” solutions, in which the system is in equilibrium and is not rotating. It is long known that if one adds energy-carrying matter fields, such as the Maxwell field of electromagnetism, then uniqueness can be violated. A clear example is a black hole that swallows charge, forcing the electric field to “turn on” in the space around the black hole. In this case, one can show that there is a static solution that describes a single charged black hole. However, it is possible to find different solutions where two or more black holes with like charges repel each other in a way that exactly counters their gravitational attraction, allowing them to be placed at rest anywhere [5]. This multi-black-hole arrangement can be chosen to have precisely the same total mass and charge as the single black hole, so that the two solutions can’t be distinguished from afar. In other words, fixing mass, and now also charge, does not dictate a unique solution to Einstein’s equation.
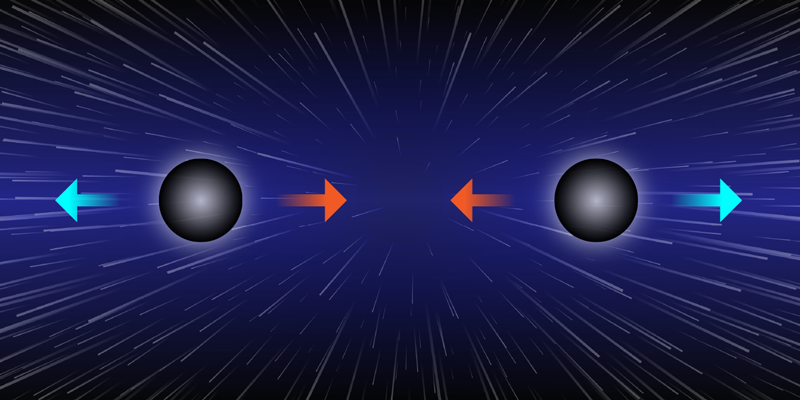
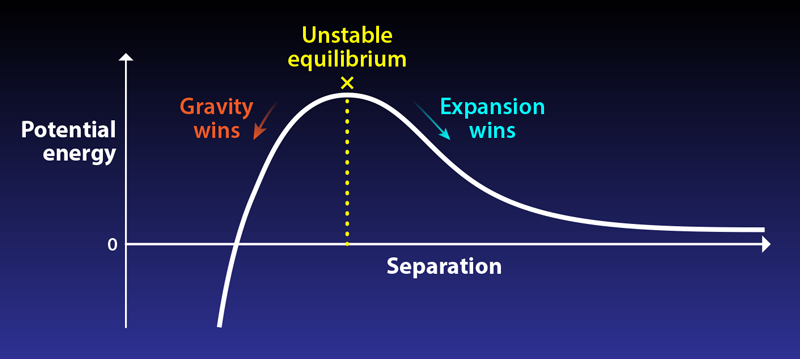
Dias and colleagues have uncovered a new violation of uniqueness. They construct new static binary-black-hole solutions in the presence of a positive cosmological constant, but no matter fields, using a similar idea to the like-charged black holes. Two black holes are positioned precisely so that their gravitational attraction is balanced by the acceleration due to the cosmological constant. These black holes can have the same total mass as a single isolated black hole, explicitly showing that fixing mass does not lead to a single unique static solution. The researchers emphasize that it is natural to think such solutions exist. If the black holes are small compared to the length scale of the cosmological constant, one may mathematically approximate them as two particles attracted by Newton’s force of gravity but repelled by a force representing the cosmological expansion. If these black holes are set up in precisely the correct way, they sit in an unstable equilibrium, akin to a pen balanced on its pointed end. Any disturbance will ruin this perfect balance.
Despite this Newtonian intuition, mathematical theorems [6, 7] have implied such binary solutions could not exist in Einstein’s theory, and no such solutions had previously been written down. This lack of solutions is not surprising, as having two black holes breaks rotational symmetry. Then Einstein’s equation takes the form of coupled, nonlinear partial-differential equations, and there seems little hope of writing simple solutions with pen and paper. The new approach taken by Dias and colleagues is to exploit numerical methods [8]. The researchers are expert in this numerical approach and achieve a technical tour de force. The results reveal that indeed these balanced two-black-hole solutions exist, and for the same masses as for the single-black-hole solution. “But wait!” I hear you say. “Didn’t theorems claim they do not exist?” While that was the expectation, Dias and colleagues point out a logical inconsistency in the proof of one theorem [6] and a limiting assumption in another [7]. In the end, they argue that there is no contradiction between the numerical solutions and the earlier theorems.
For the first time, uniqueness is claimed to fail for solutions to Einstein’s equation in the absence of matter fields. This failure requires a positive cosmological constant, an energy component that could explain the Universe’s accelerated expansion. These new exotic static binary black holes are thought to be unstable equilibria and therefore not expected to be relevant in nature. However, Dias and colleagues point out that when the black holes are allowed to rotate, it is possible that their spin interaction may stabilize the solutions. This raises the fascinating possibility of having an isolated pair of solar-mass black holes in our Universe, balancing happily a few hundred light years apart and impossible to distinguish from a single black hole from far away. In any event, our understanding of the important uniqueness properties of Einstein’s equation has been significantly advanced in this work.
References
- P. T. Chruściel et al., “Stationary black holes: Uniqueness and beyond,” Living Rev. Relativ. 15, 7 (2012).
- R. P. Kerr, “Gravitational field of a spinning mass as an example of algebraically special metrics,” Phys. Rev. Lett. 11, 237 (1963), .
- Ó. J. C. Dias et al., “Static black binaries in de Sitter space,” Phys. Rev. Lett. 131, 131401 (2023).
- S. W. Hawking, “Breakdown of predictability in gravitational collapse,” Phys. Rev. D 14, 2460 (1976).
- S. D. Majumdar, “A class of exact solutions of Einstein's field equations,” Phys. Rev. 72, 390 (1947); A. Papapetrou, “A Static solution of the equations of the gravitational field for an arbitrary charge distribution,” Proc. R. Ir. Acad., Sect. A A51, 191 (1947).
- A. ul Alam and W. Yu, “Uniqueness of de Sitter and Schwarzschild-de Sitter spacetimes,” Commun. Anal. Geom. 23, 377 (2015).
- P. LeFloch and L. Rozoy, “Uniqueness of Kottler spacetime and the Besse conjecture,” C. R. Math. 348, 1129 (2010); S. Borghini et al., “On the uniqueness of Schwarzschild-de Sitter spacetime,” arXiv:1909.05941.
- T. Wiseman, “Numerical construction of static and stationary black holes,” arXiv:1107.5513.