Matching a Measurement to a Quantum State
A quantum sensor is a device that can leverage quantum behaviors, such as quantum entanglement, coherence, and superposition, to enhance the measurement capabilities of a classical detector [1–5]. For example, the LIGO gravitational-wave detector employs entangled states of light to improve the distance-measurement capabilities of its interferometer arms, allowing the detection of distance changes 10,000 times smaller than the width of a proton. Typically, quantum sensors use systems prepared in special quantum states known as probe states. Finding the ideal probe state for a given measurement is a focus of many research endeavors. Now Jarrod Reilly of the University of Colorado Boulder and his colleagues have developed a new framework for optimizing this search [6]. The approach could aid in developing quantum sensors that surpass the standard quantum limit—the minimum noise level of a device that can be obtained without special quantum-state preparation—and so could dramatically increase measurement sensitivity [7–9].
The capabilities of quantum sensors are rapidly expanding, and they are increasingly finding their way from laboratories to the real world. As such, the technology is poised to play a significant role in myriad fields. Quantum sensors can detect parameters ranging from magnetic fields to temperatures, and they are expected to enhance the sensitivities of devices including single-photon detectors; laser imaging, detection, and ranging (lidar) detectors; and atomic clocks, which are fundamental to global positioning systems.
In many devices, the quantum sensor plays a crucial role in parameter estimation. Generally, quantum parameter estimation consists of three steps: First, the quantum system, such as a qubit or a collection of qubits, is prepared in its optimal probe state. Second, the probe state undergoes a unitary evolution, a step also known as quantum evolution. This unitary evolution can be thought of as “sensitivity tuning” where the probe state changes based on the value of the parameter of interest. This step thus encodes information about the parameter into the probe state. Third, an optimal measurement is executed and information about the parameter extracted.
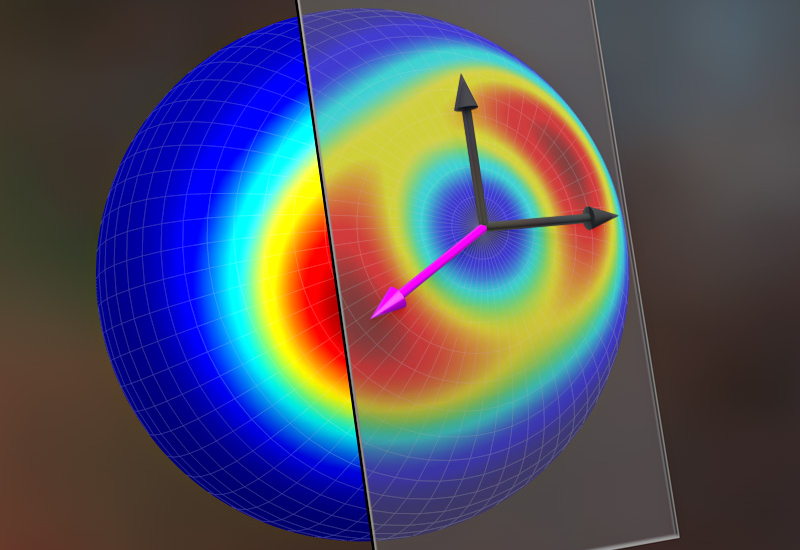
How to find the optimal probe state for a specific system or parameter of interest is a problem on which the quantum sensor community is increasingly focusing. For a given quantum sensor, the decision of which probe state to use is typically done by searching for the state with the maximal quantum Fisher information (QFI). QFI is the quantum analog of Fisher information, which measures the information some observable carries about some unknown parameter. A quantum probe state’s QFI evaluates its sensitivity to variations in the parameter of interest, and so is regarded as a key indicator of the reliability of that state when used in a quantum sensor. The higher a probe state’s QFI, the more accurate the measurement of the parameter of interest should be.
The method of Reilly and his colleagues flips that search protocol on its head. Rather than hunting for the best probe state for a given measurement, their framework finds the best measurement for a given probe state. This approach, which also uses QFI, allows them to assess the full potential of a given probe state for all quantum sensing applications. In their approach, the researchers take their probe state. Then they determine its QFI matrix (QFIM). Diagonalizing that matrix, they show that they can identify the optimal generator for that probe state for a specific quantum sensing purpose. The generator can thus be thought of as the specific measurement or quantum operation that when applied to a quantum probe state will maximize the estimation precision parameters related to the system being measured.
To understand more broadly how the method works, consider the problem of trying to find the longest route that a ball rolling down a hill can traverse in a fixed time period. In the classical world, the answer is simple—the path will map the route with the steepest slopes—so the search requires finding that path. In the quantum world, the answer is more complex. Quantum hills exist in enormous numbers of dimensions, making brute force searches intractable. But Reilly and colleagues’ method follows an idea similar to the classical one—it finds some optimal trajectory of the probe state through space and time in a way reminiscent of how classical general relativity can predict light paths by finding optimal trajectories through curved space-time. Using geometrical concepts, they determine which transformations cause a specific entangled quantum system to evolve in the fastest way and, therefore, which parameters the state is most sensitive to.
As well as improving current quantum sensors, the method of Reilly and colleagues has the potential to open the door for the use of quantum sensors for multiparameter estimation, which is required in many imaging and metrology applications. Their proposal introduces a novel perspective on quantum sensing by emphasizing the importance of high-precision measurements for choosing the right generator for a given quantum state. Research and development in this area will likely lead to innovative breakthroughs in the coming years, driving advancements in quantum technology and in our understanding of quantum mechanics.
References
- S. L. Braunstein and C. M. Caves, “Statistical distance and the geometry of quantum states,” Phys. Rev. Lett. 72 (1994).
- M. G. A. Paris, “Quantum estimation for quantum technology,” Int. J. Quantum Inform. 07, 125 (2009).
- V. Giovannetti et al., “Quantum Metrology,” Phys. Rev. Lett. 96 (2006).
- V. Giovannetti et al., “Advances in quantum metrology,” Nature Photon 5 (2011).
- V. Giovannetti et al., “Quantum-enhanced measurements: Beating the standard quantum limit,” Science 306 (2004).
- J. T. Reilly et al., “Optimal generators for quantum sensing,” Phys. Rev. Lett. 131, 150802 (2023).
- B. Teklu et al., “Bayesian estimation of one-parameter qubit gates,” J. Phys. B: At. Mol. Opt. Phys. 42 (2009).
- D. Brivio et al., “Experimental estimation of one-parameter qubit gates in the presence of phase diffusion,” Phys. Rev. A 81 (2010).
- M. G. Genoni et al., “Optical phase estimation in the presence of phase diffusion,” Phys. Rev. Lett. 106 (2011).