Why It’s Hard to Break Plastics
Plastics and other polymer materials are often very resistant to cracking—a fact that models have not been able to accurately capture. Now a research team has developed a model of polymer fracture that explains how these materials remain intact under intense stretching. [1]. The key to the model is that it accounts for polymer chains that extend deep within the material and that can share the strain that would break a material with more localized chains. The insights could lead to the development of new structures with an enhanced resistance to shocks.
Researchers typically study fracture by cutting a small notch or crack into a material and then pulling it apart. The amount of work required to enlarge the crack is called the fracture energy. For most materials, the fracture energy is equal to the energy it takes to break the molecular bonds located along the crack tip, where the enlargement occurs. For polymers, the situation is more complex, as the molecules are long chains. In the 1960s, theorists came up with a model of polymer fracture based on the rupture of individual chains at the crack tip [2]. “The problem is that this model underestimates by a factor of 10 to 100 the energy required to fracture a polymer material,” says Xuanhe Zhao from the Massachusetts Institute of Technology.
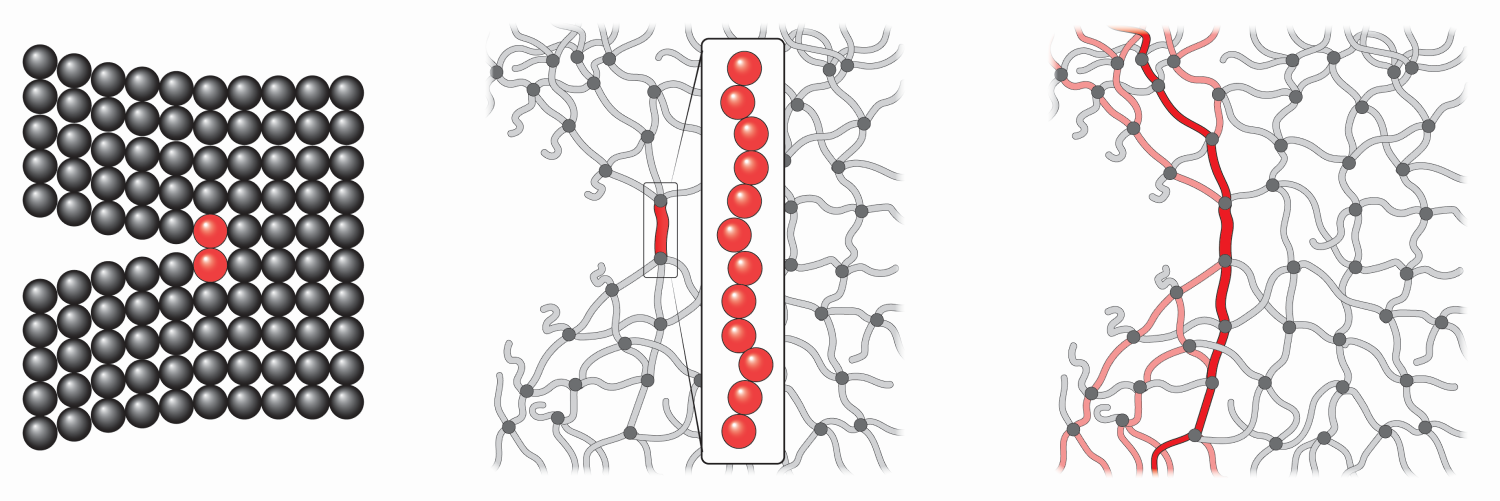
Zhao and his colleagues have tackled this problem by considering a polymer as a network of interconnected chains. Each chain is modeled as a long spring with a stiffness that varies as the chain is stretched. Initially, the chain is coiled like a floppy piece of string, and pulling it apart is relatively easy. But once the chain is pulled straight, it becomes much more resistant to further lengthening. This big jump in stiffness has been captured in previous polymer models, but no one had yet incorporated this behavior into a model of polymer fracture, Zhao says.
The team simulated a variety of polymer networks with a range of different geometries and stiffness values. In each case, they inserted an initial crack and then simulated a force that tries to widen the crack, mimicking fracture experiments. They found that the fracture energy was at least 10 times larger than that predicted in previous models. To understand this improved performance, the researchers looked at where the pulling energy is released within the material after the crack is enlarged. The simulations showed that this “dissipation” energy extended over a wide region within the polymer network. This behavior contrasts with previous models in which the dissipation has been localized around the crack tip.
Zhao explains the extended dissipation as the result of “shared stretching” across neighboring chains. A single chain at the crack tip is connected to a large number of chains that branch out from the tip. As the material is initially pulled apart, the tip chain uncoils and straightens. More pulling would normally cause it to break, but the tip chain instead starts pulling on its neighbors, causing them to stretch. When the tip chain finally snaps, all those neighbors relax by recoiling, Zhao says.
To support the conclusions of their simulations, the researchers performed experiments with a plastic sheet that they patterned to resemble a polymer network. The pattern consisted of multiple zigzag-shaped elements that behave like macroscopic versions of coiled polymer chains. When the two ends of one of these zigzag elements are pulled apart, the Z shape unfurls easily at first, but then the element becomes stiff when pulled straight. The team cut an initial crack in the sheet and then observed how it responded to a crack-widening force. The experimental results were consistent with the simulations in that the stretching was shared over a large neighborhood of zigzag elements.
To go further, the team plans to perform simulations that more accurately account for the disordered geometry within a real polymer network. They are also designing metamaterials—materials whose properties are based on their macroscopic structure rather than on their chemical composition—inspired by the principles of their polymer model. “If you design each segment like this, then you can dramatically enhance the intrinsic fracture toughness of your metamaterials,” Zhao says. He foresees these metamaterials being used as shock absorbers in items such as car seat cushions.
“Polymer fracture is ubiquitous in physical systems, but it is a complex phenomenon,” says soft matter researcher John Kolinski from the Swiss Federal Institute of Technology in Lausanne (EPFL). The new work helps explain this phenomenon by identifying a key mechanism: the storing of strain energy in an extended region of stiffened polymer chains. “The researchers use a combination of simple experiments and numerical calculations that clearly demonstrate this mechanism,” Kolinski says.
–Michael Schirber
Michael Schirber is a Corresponding Editor for Physics Magazine based in Lyon, France.
References
- B. Deng et al., “Nonlocal intrinsic fracture energy of polymerlike networks,” Phys. Rev. Lett. 131, 228102 (2023).
- G. Lake and A. Thomas, “The strength of highly elastic materials,” Proc. R. Soc. London, Ser. A 300, 108 (1967).