Might There Be No Quantum Gravity After All?
Physicists’ best theory of matter is quantum mechanics, which describes the discrete (quantized) behavior of microscopic particles via wave equations. Their best theory of gravity is general relativity, which describes the continuous (classical) motion of massive bodies via space-time curvature. These two highly successful theories appear fundamentally at odds over the nature of space-time: quantum wave equations are defined on a fixed space-time, but general relativity says that space-time is dynamic—curving in response to the distribution of matter. Most attempts to solve this tension have focused on quantizing gravity, with the two leading proposals being string theory and loop quantum gravity. But new theoretical work by Jonathan Oppenheim at University College London proposes an alternative: leave gravity as a classical theory and couple it to quantum theory through a probabilistic mechanism [1]. Such a hybrid strategy was traditionally considered a nonstarter, as it was thought to lead to inconsistencies [2]. Oppenheim avoids these pitfalls, but at the cost of having to insert probability—a “roll of dice”—into the evolution of space-time. Future experiments could test the viability of this approach by probing whether gravity is quantum.
For the past 70 years one of the most important problems in fundamental physics has been to reconcile quantum physics with general relativity. There are two strategies for this unification: either quantize gravity or find a way to insert quantum matter into a classical gravitational framework. The former is clearly favored, but none of the quantum-gravity proposals have yet been experimentally confirmed. That would seem to leave an opening for the other strategy, but theorists have shown—through so-called no-go theorems—that coupling quantum matter to classical gravity leads to inconsistencies, such as violations of the famed Heisenberg uncertainty principle. Indeed, the best-known model for this quantum-to-classical coupling, the semiclassical Einstein equation [3], suffers from the inconsistencies predicted by these no-go theorems.
With his new approach, Oppenheim avoids the barriers of the no-go theorems by abandoning one of their underlying assumptions: that the coupling between classical gravity and quantum matter is reversible [4]. In a reversible theory, the state of the system at any given time can be used, together with the equations of motion, to uniquely determine the state of the system at any other time in the past or the future. However, not all theories need be reversible, they can also be stochastic. In a stochastic theory, the initial state of a physical system evolves according to an equation, but one can only know probabilistically which states might occur in the future—there is no unique state that one can predict.
Oppenheim develops a stochastic theory that relies on two separate statistical approaches for the quantum and classical parts of a system. In the statistical description of the quantum side, states are described using density operators that evolve as if the system were open—that is, susceptible to uncontrolled influences from the environment. In the statistical description of the classical side, states are probability distributions on phase space—a framework that is often used to model large numbers of particles, where one does not know the individual position and momentum of each particle.
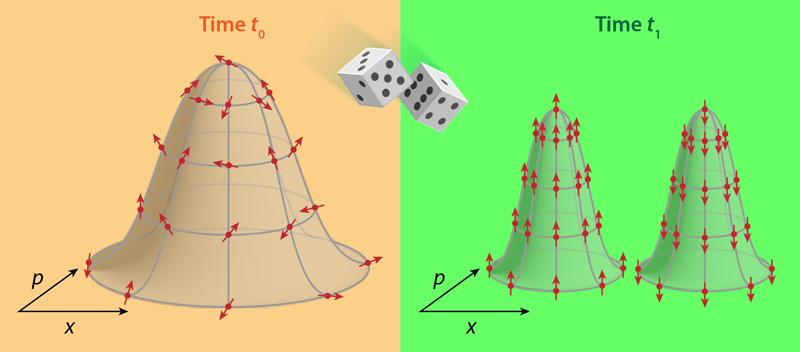
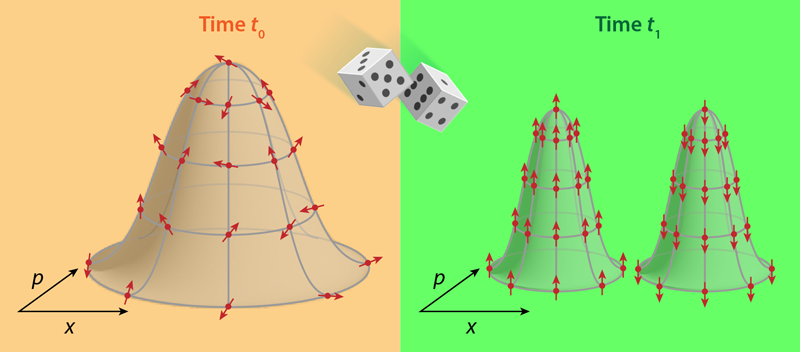
Oppenheim unites these two statistical descriptions in a classical quantum state, which consists of a classical probability distribution over phase space, combined with a quantum density operator that is defined at each point of that phase space (Fig. 1). For example, a particle might have a 15% probability of being in some region of phase space, and its spin state in that region might be an equal superposition of up and down states.
The next step is to derive a general equation for the coupling between the classical and quantum systems of the classical quantum state. Unlike previous (reversible) couplings, Oppenheim’s stochastic coupling does not mix quantum and classical features: it preserves the nature of each system. For example, the coupling ensures no violations of the uncertainty principle in the quantum system, as well as no faster-than-light signaling in the classical system. The resulting equation has multiple parts: a reversible Hamiltonian evolution for both the classical and quantum systems, decoherence of the quantum system, as well as probabilistic “jumps” between states. Such jumps can correspond to a measurement that splits the probability distribution of a particle into two parts, one corresponding to each measurement outcome.
Having determined the general form of classical–quantum couplings, Oppenheim turns his attention to coupling quantum field theory (QFT) to general relativity. Specifically, quantum fields on curved space-time are coupled to the classical metric of general relativity using the stochastic coupling equation. General relativity then imposes further constraints on the form of this general equation. A first requirement is that there exists a classical limit in which the standard equations of motion of general relativity are recovered. A second is that the laws of physics look the same for all observers. From these requirements, Oppenheim obtains a hybrid theory that features stochastic backreaction of the fields on the curved space-time; in other words, the quantum fields can change the curvature of the space-time as one would require from a unification of general relativity and QFT. Existing approaches to QFT do not have this feature—they treat the curvature as fixed. The new model therefore has the potential to describe a fundamental interaction between QFT and general relativity.
Oppenheim’s proposal is in a sense very radical: it flies in the face of 70 years of accepted wisdom of the fundamental physics community. Yet in another sense it is very conservative: it preserves the classical nature of general relativity and thus neatly avoids the host of conceptual difficulties facing existing unification proposals. For instance, space-time determines the causal relations between events, and any theory that quantizes space-time faces the problem of what it means for causal structure to have quantum properties, such as superpositions of causal orders. But trading quantumness for stochasticity has its own conceptual difficulties. For example, Oppenheim finds that quantum information can be lost in a black hole, a result that many physicists might find unacceptable. There are also fundamental questions about the origin of the probabilistic jumps.
So what’s next for this new theory of quantum matter and classical gravity? As with all physical theories, the true test lies in its agreement with experimental data. The model can be constrained by measurements of the coherence time of a massive object in a quantum superposition, as the coherence time can be related to the evolution of the space-time metric. Existing coherence-time data have already been used to rule out certain parameter ranges for classical–quantum hybrid models such as Oppenheim’s [5]. An even more decisive empirical test of these models could come from proposals to experimentally determine if the gravitational field is classical [6, 7] (see Synopsis: A Test of Gravity’s Quantum Side). The idea is to entangle two massive objects with just their gravitational interaction, which would imply that gravity is quantum at its base. Experimental groups are currently at work trying to improve their setups in order to be able to carry out these experiments. The race is on to determine whether this new proposal will win out over the established approaches.
References
- J. Oppenheim, “A postquantum theory of classical gravity?” Phys. Rev. X 13, 041040 (2023).
- C. M. DeWitt and D. Rickles, The Role of Gravitation in Physics: Report from the 1957 Chapel Hill Conference, Vol. 5 (Max Planck Institute for the History of Science, Berlin, 2011).
- C. Møller, “The energy-momentum complex in general relativity,” Relativistic Theories of Gravitation, edited by A. Lichnerowicz and M. A. Tonnelat Colloq. Int. CNRS Vol. 91 (1962).
- T. D. Galley et al., “Any consistent coupling between classical gravity and quantum matter is fundamentally irreversible,” Quantum 7, 1142 (2023).
- J. Oppenheim et al., “Gravitationally induced decoherence vs space-time diffusion: testing the quantum nature of gravity,” (2022) arXiv:2203.01982.
- S. Bose et al., “Spin entanglement witness for quantum gravity,” Phys. Rev. Lett. 119, 240401 (2017).
- C. Marletto and V. Vedral, “Gravitationally induced entanglement between two massive particles is sufficient evidence of quantum effects in gravity,” Phys. Rev. Lett. 119, 240402 (2017).