Finding Nonlinearities in Black Hole Ringdowns
“Spacetime tells matter how to move; matter tells spacetime how to curve.” This statement by physicist John Wheeler captures a defining feature of general relativity: its prediction of nonlinear spacetime dynamics. Such nonlinear evolution should be most evident in energetic spacetime events such as merging black holes, prompting the question of whether we can test for it using observations of gravitational waves emitted during such mergers. Two independent teams, led by Keefe Mitman at the California Institute of Technology [1] and Mark Ho-Yeuk Cheung at Johns Hopkins University in Maryland [2], show that this is the case. Using numerical simulations, they show the presence of nonlinearity in postmerger gravitational-wave signals. The result suggests that gravitational waves from black hole mergers are a promising place to search for the imprints of nonlinearity, offering a way to test our understanding of gravity in strong, nonlinear regimes.
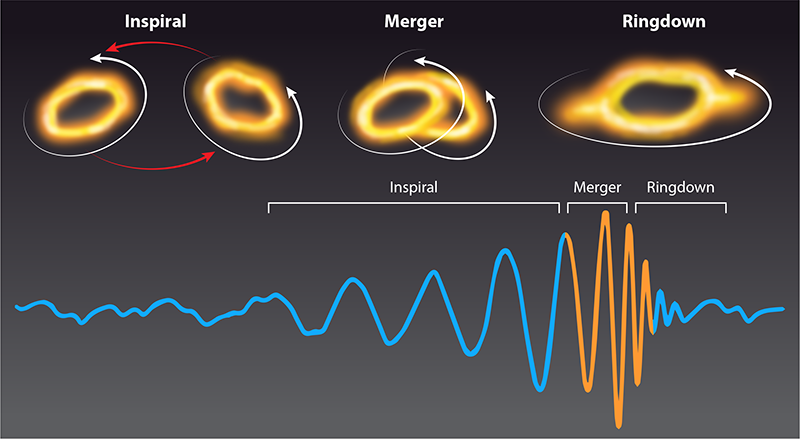
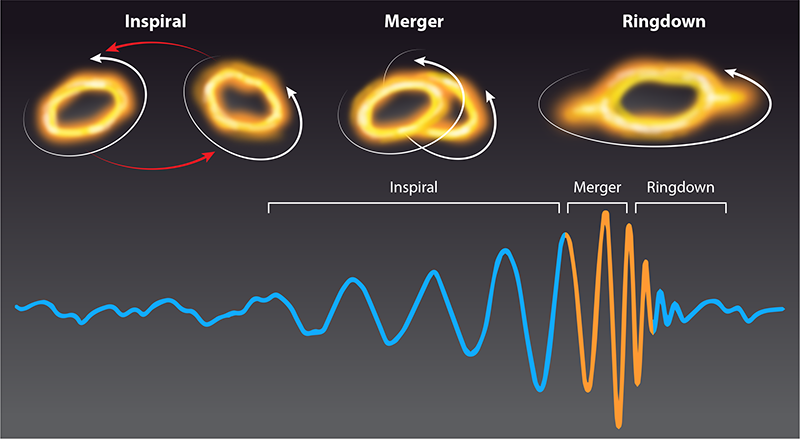
The dominant sources of signals observed by the LIGO, Virgo, and KAGRA gravitational-wave detectors are mergers of binary black holes in quasicircular orbits [3]. In numerical-relativity simulations of such systems, we can quantify the presence of significant nonlinearities in the region near the black holes during the merger and in the early stages of the postmerger phase [4] (Fig. 1). But whether these nonlinearities are manifest at a detectable level in gravitational-wave observations is an open question.
A pioneering study led by Matthew Giesler of the California Institute of Technology and colleagues [5] discovered that all of the postmerger features in a numerical relativity simulation of a black hole merger could be captured by superposition of linear-perturbation modes, that is, without accounting for nonlinearity that is seen near the black holes. This result incited considerable debate over whether the model is sufficiently flexible to phenomenologically capture the signal features or whether the imprints of nonlinearity are truly lost as the gravitational waves propagate far away from the black hole. The result was also perplexing because it appeared to contradict an earlier study [6], which found that, for the easier-to-simulate case of a head-on collision between black holes, linear perturbation was insufficient to describe postmerger signals.
When black holes merge, the remnant black hole is highly distorted; it gradually relaxes during a phase called the ringdown. During coalescence and in the early ringdown phase, the dynamics are expected to be governed by nonlinear evolution of the spacetime close to the black hole. Subsequently, however, the dynamics can be approximated as the evolution of perturbations on the remnant black hole’s spacetime. Just as a struck bell vibrates at its normal-mode frequencies, a perturbed black hole emits gravitational waves, which contain modes with a complex frequency spectrum characteristic of the black hole in this phase. Ringdowns can be analytically modeled as linear superpositions of damped sinusoids consisting of these characteristic frequency spectra. The modes are indexed by two angular numbers (l, m)—corresponding to the spherical harmonic basis functions onto which the ringdown is decomposed—and by an overtone index (n).
Mitman, Cheung, and their colleagues look for nonlinearity in a set of numerical relativity simulations of quasicircular binary black hole mergers produced by the Simulating eXtreme Spacetimes (SXS) Collaboration [7]. One way to spot nonlinearity in such a system is to find the second-order perturbation modes, which arise as an effect of the first-order modes interacting with themselves. At the first order, a quasicircular binary merger dominantly excites the (2, 2) linear perturbation mode. This implies that the dominant (and therefore easiest to detect) second-order mode would be seen in the (4, 4) mode. Some characteristic features of the second-order mode in (4, 4) are the following: the mode frequency is twice that of the (2, 2) mode, its amplitude is proportional to the square of the (2, 2) mode amplitude, and its phase is twice that of the (2, 2) mode shifted by a constant factor.
To find a mode that exhibits the above properties in the (4, 4) mode, the researchers perform numerical fits to the (4, 4) mode in a set of numerical simulations. In addition to the superposition of damped sinusoids corresponding to the first-order perturbation spectrum that researchers typically use, they include an additional free mode in their ringdown model. They show that this free mode picks the second-order mode frequency, considerably improving the fit of the ringdown model to the (4, 4) mode for all of the numerical simulations used.
To ensure that this improvement is not an overfitting artifact, they show that the amplitudes and phases of the sinusoids are stable under different choices of start time in their fit (allowing for the decay of the amplitudes over time). In addition, both studies show that the second-order mode amplitude is proportional to the square of the linear amplitude, as expected. This is convincing evidence for the second-order perturbation mode in ringdowns, showing that nonlinearities in the spacetime dynamics occurring in strong-field regimes near black holes propagate outward, and should manifest in the gravitational-wave signals detected billions of light years away.
In contrast to the dynamics during black hole coalescence, which are also likely governed by nonlinear dynamics, ringdowns are valuable for designing tests of gravity because we understand them analytically. Such tests could be conducted with next-generation ground-based detectors such as the Cosmic Explorer and the Einstein Telescope, which might be able to measure the second-order modes.
Finally, the peak amplitude of the second-order mode is comparable to or larger than the (4, 4) linear perturbation amplitude across the simulation set studied by the two teams. Therefore, not including this mode in the ringdown modeling might lead to biases in the estimates of the black holes’ parameters—such as their spin and mass—especially in gravitational-wave signals with high signal-to-noise-ratio ringdowns. This is an important insight for building analysis infrastructure for next-generation detectors.
References
- K. Mitman et al., “Nonlinearities in black hole ringdowns,” Phys. Rev. Lett. 130, 081402 (2023).
- M. H.-Y. Cheung et al., “Nonlinear effects in black hole ringdown,” Phys. Rev. Lett. 130, 081401 (2023).
- R. Abbott et al. (LIGO Scientific Collaboration, Virgo Collaboration, and KAGRA Collaboration), “GWTC-3: Compact binary coalescences observed by LIGO and Virgo during the second part of the third observing run,” arXiv:arxiv:2111.03606.
- S. Bhagwat et al., “On choosing the start time of binary black hole ringdowns,” Phys. Rev. D 97, 104065 (2018).
- M. Giesler et al., “Black hole ringdown: The importance of overtones,” Phys. Rev. X 9, 041060 (2019).
- R. J. Gleiser et al., “Colliding black holes: How far can the close approximation go?” Phys. Rev. Lett. 77, 4483 (1996).
- M. Boyle et al., “The SXS collaboration catalog of binary black hole simulations,” Classical Quantum Gravity 36, 195006 (2019).
- B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), “Observation of gravitational waves from a binary black hole merger,” Phys. Rev. Lett. 116, 061102 (2016).