Organelle Building Codes
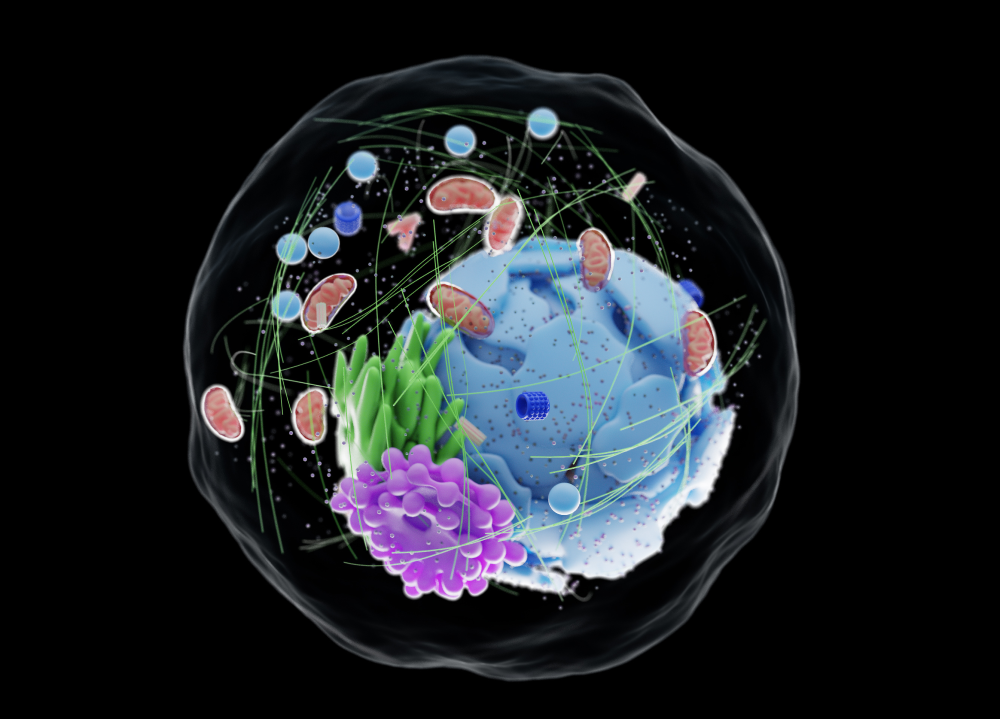
Biologists have identified within cells many specialized structures called organelles that carry out crucial tasks, but how cells regulate the size and the number of organelles has remained a puzzle. Now, using simulations backed by experiments, biophysicists have demonstrated that cells appear to produce organelles through a seemingly erratic, or “bursty,” growth process, which enables them to control average organelle sizes and numbers while also constraining organelle size variations within any cell [1]. The work helps to build up a more fundamental understanding of the mechanisms of cellular function.
The list of organelles includes lipid droplets, which store fat, and mitochondria, which generate chemical energy. Because the size of an organelle strongly influences how molecules diffuse across its boundaries, cells need to regulate both the size and the number of organelles with precision. In one standard view, organelles have a limited supply of building materials, and they grow continuously until those materials run out. This “limiting-pool” model predicts organelles of a relatively uniform size, with the average size of the organelles in a particular cell being roughly the same as that in other cells having the same number of organelles. But organelles within a single cell can vary from this average—something that current models have not addressed.
Shankar Mukherji of Washington University in St. Louis and his colleagues have investigated the size variations of organelles. Their approach considers the rate that cells construct components. “We wondered if organelle growth, far from being an orderly ‘brick-by-brick’ assembly, might occur in more random bursts,” Mukherji says.
To explore this idea, they began by simulating the limiting-pool model, as well as two alternative models for how organelles might grow by assembly from basic components. In the simulations, the number of organelles can increase through synthesis of a new organelle or through splitting of an existing organelle into two. The number of organelles can also decrease through mergers. For each model, a relationship was found between the average size and the number of organelles. The two alternative models predicted constant organelle size, regardless of numbers, and the limiting-pool model predicted that the size should gradually fall with increasing numbers of organelles.
Mukherji and colleagues then compared these model results to measurements of organelles in real cells of the yeast Saccharomyces cerevisiae, using a fluorescent protein to mark the organelle membranes. Analyzing images of three specific types of organelles—Golgi apparatuses, lipid droplets, and peroxisomes—they found that the limiting-pool model worked best in predicting the observed relationship between average size and number of organelles.
However, closer study revealed a significant disagreement between theory and experiment over the organelle size variations. In measurements in real cells, the researchers found that the variations were constant—always around 50% of the average organelle size. This observation conflicts with the limiting-pool model, which predicts that the relative size of intracellular variations should be greater in cells with smaller organelles.
To address this discrepancy, the team altered the limiting-pool model, using inspiration from earlier work. This new model assumes that organelles grow from a pool of building blocks in occasional bursts rather than at a steady rate. The bursts have random amplitude—where the amplitude corresponds to the amount of building blocks used. In a series of simulations with this model, the researchers again found that organelle average size decreased with increasing numbers, reflecting the limiting-pool growth. But they also found that the growth dynamics now led to much smaller variations in organelle size—just as seen in the real cells. The burst model can thus explain how cells balance organelle sizes and numbers while also keeping size fluctuations within a narrow window, Mukherji says.
The burst model also provides an explanation for why the organelles have different size distributions. For example, the Golgi apparatuses typically have larger average sizes and larger size variations than the peroxisomes. According to the burst model, these distinctions reflect differences in the frequency and amplitude of bursts. Specifically, Golgi bursts are expected to have larger amplitudes but smaller frequencies than peroxisomes. The researchers showed, however, that they could rescale their organelle data in such a way that all the distributions could be fit with a single curve. This “universal” behavior suggests that the burst mechanism underlies all organelle growth, despite the fact that each organelle has a unique building process.
“The question of how cells control the sizes of their organelles is as old as cell biology,” says biophysicist Jané Kondev of Brandeis University in Massachusetts. He says that the new study has made careful measurements of organelle size distributions, revealing universal size variations that could indicate a common growth mechanism. “I’m excited to see how much we learn about morphogenesis in cells from studies like this,” he adds.
–Mark Buchanan
Mark Buchanan is a freelance science writer who splits his time between Abergavenny, UK, and Notre Dame de Courson, France.
References
- K. P. Amiri et al., “Robustness and universality in organelle size control,” Phys. Rev. Lett. 130, 018401 (2023).