Quantum Phase Transition Predicted for Gaseous Water
The water molecule is a relatively simple system, composed of two hydrogen atoms and one oxygen atom. Put enough of these molecules together and they condense into liquid water, which, unlike individual water molecules, exhibits highly complex behavior [1]. Now researchers predict that water can also display exotic behavior in the gas phase—where the molecules effectively exist in isolation [2]. In simulations they find that a chain of gaseous water molecules can switch from having random orientations to having highly correlated ones. This so-called quantum phase transition indicates that the water molecule could be a candidate system for future quantum information processing devices.
It is impossible to discuss liquid water without mentioning hydrogen bonds, which bind water molecules together to form liquid water and ice. Much of the complex behavior of water molecules originates from the interplay of these hydrogen bonds with the van der Waals interactions between the molecules. Another very important property of water is the permanent dipole moment of its molecules. The strength of water’s dipole moment is such that water molecules that are far enough apart to be free of the pull of a hydrogen bond can still be close enough to experience the attraction of an intermolecular dipolar interaction, which can impact the phase behavior of the system. These dipolar interactions have recently been exploited to observe interesting quantum phenomena in optical lattices [3].
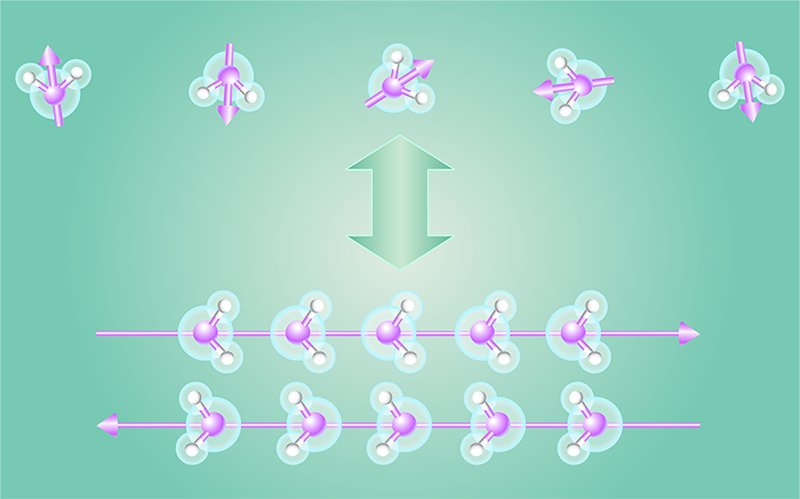
Motivated by this finding, Tobias Serwatka of the University of Waterloo, Canada, and his colleagues performed simulations of a linear chain of water molecules—a line of molecules that are far enough apart that they aren’t hydrogen bonded to one another (Fig. 1). They then computed the phase diagram of this chain, which involved finding the ground and excited orientational states of the molecules as a function of the molecule separation.
Serwatka and colleagues find that when they increase the linear density of water molecules in the chain, the chain undergoes a phase transition from being fully disordered to being a fully ordered line of dipoles, a 1D ferroelectric system. However, the degeneracy of their solution means that the actual ground state of the chain is antiferroelectric—the ground state is a linear combination of the two polarization directions of the dipoles (Fig. 1).
The parameter controlling this transition is the linear density of the water molecules. The phase transition occurs when the temperature of the system is exactly 0 K, eliminating any influence of thermal fluctuations. The entropy of the system is also zero. Thus, the order-to-disorder transition can only be driven by quantum fluctuations. The nature of the phase transition is further evidenced by the team’s identification of two order parameters—quantities that characterize the scaling of the system at the phase transition. Using a purely quantum order parameter and a purely classical one, the team shows that the waterline is in the so-called 1 + 1 Ising universality class.
Serwatka and colleagues envision using the orientational states in a water chain to encode quantum information in a future water-based quantum device. But realizing a dipole-locked chain will be challenging. Researchers have experimentally created 1D water-molecule chains by confining the molecules in a carbon nanotube [4]. But the water molecules tend to approach each other, allowing hydrogen bonds to form and erase the dipole alignment. To prevent this bonding, researchers can “pin” the molecules in place by encapsulating them in a 1D, hydrophobic crystal matrix. However, the electrons in such a matrix could also screen the very weak dipolar interactions between the water molecules that give rise to the predicted quantum phase transition. But even with this caveat, the results are still important and will likely be explored further by those developing quantum technology devices.
Regardless of whether the simulations can be experimentally realized, the results of Serwatka and his colleagues add to the body of work showing that the behavior of solid, liquid, and gaseous water is incredibly rich and physically connected: there are common behaviors in water’s phase transitions across the matter states (solid, liquid, gas) and the possible regimes (quantum or classical). For example, it is now widely confirmed that, at atmospheric pressure, the ground state of ice XI also undergoes a ferroelectric order–disorder phase transition, but this one is thermally driven, occurs at around 70 K, and involves hydrogen bonds [5, 6]. In such classical cases, the different phases are characterized by well-defined hydrogen-bonding patterns, but the various phenomena only occur because of the permanent dipole of water molecules. Whatever aspect of water researchers study next, one thing we can be certain of is that new, unexpected discoveries will keep coming—and making a splash.
References
- E. Brini et al., “How water’s properties are encoded in its molecular structure and energies,” Chem. Rev. 117, 12385 (2017).
- T. Serwatka, “Quantum phase transition in the one-dimensional water chain,” Phys. Rev. Lett. 130, 026201 (2023).
- X. Zhang et al., “Observation of quantum criticality with ultracold atoms in optical lattices,” Science 335, 1070 (2012).
- X. Ma et al., “Quasiphase transition in a single file of water molecules encapsulated in (6,5) carbon nanotubes observed by temperature-dependent photoluminescence spectroscopy,” Phys. Rev. Lett. 118, 027402 (2017).
- Y. Tajima et al., “Phase transition in KOH-doped hexagonal ice,” Nature 299, 810 (1982).
- B. Pamuk et al., “Electronic and nuclear quantum effects on the ice XI/ice Ih phase transition,” Phys. Rev. B 92, 134105 (2015).