Memory of Blood Cells
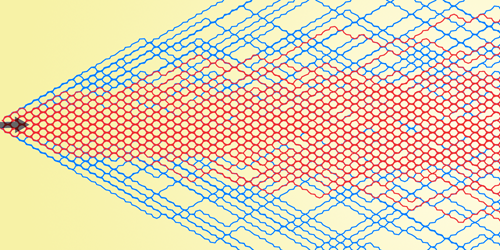
Blood flowing through arteries obeys simple fluid-dynamical equations. But from these large vessels branch progressively smaller ones, and in the tiniest vessels of all—capillaries, which are barely larger than red blood cells—the fluid equations are no longer valid. To obtain a better description of blood flow in such vessels, Chaouqi Misbah of Grenoble Alpes University in France and his colleagues numerically analyzed a system of particles traveling through a network of microchannels [1]. They found that the speed at which the particles spread through the lattice is governed by the particles’ concentration and deformability.
The researchers modeled a honeycomb lattice through which irregularly shaped, deformable particles traveled from top to bottom. When a particle encountered a fork, it could “choose” either the right or left channel. In a typical fluid—one in which the particles are very small relative to the channel width—the choice a particle makes is random and independent of its previous choices. This “random walk” causes the fluid to diffuse laterally as it moves through the network. But Misbah and his colleagues found that at low concentrations, irregularly shaped, stiff particles had a strong memory: if a particle chose the left fork previously, it strongly preferred to choose left again. Consequently, a fluid of such particles exhibited “superdiffusion,” spreading laterally much faster than in the random-walk case. If the researchers made the particles squishy, the memory effect wasn’t as strong, but the fluid still expanded outward faster than usual.
Misbah thinks that the role that particles’ stiffness and shape play on particle transport could have implications for diseases that affect red blood cells, such as sickle cell anemia and malaria.
–Katie McCormick
Katie McCormick is a freelance science writer based in Sacramento, California.
References
- Z. Shen et al., “Anomalous diffusion of deformable particles in a honeycomb network,” Phys. Rev. Lett. 130, 014001 (2023).