How Earth’s Magnetic Field Influences Flows in the Planet’s Core
Earth’s inner core is a hot, solid ball—about 20% of Earth’s radius—made of an iron alloy. The planet’s outer core, beneath the rocky mantle, is a colder, liquid metal. Geophysics models explain that, since the movement of a liquid metal induces electrical currents, and currents induce a magnetic field, convection and rotation produce our planet’s magnetic fields. But these models typically neglect an important contribution: how Earth’s magnetic field influences the very flows that generate it. Alban Pothérat of Coventry University, UK, and collaborators have now developed a theory that accounts for such feedback and vetted it using a lab-based “Little Earth Experiment” [1]. Their results inform a model pinpointing processes that might explain the discrepancies between theoretical predictions and satellite observations of Earth, opening new perspectives on the study of geophysical flows.
Understanding flows in planetary interiors is a long-standing challenge. “If you don’t account for the fact that the magnetic field itself changes the flow, then you won’t get the right flow,” says Pothérat. Indeed, both satellite data from the European Space Agency’s Swarm mission and state-of-the-art numerical simulations indicate certain circulating core flows where liquid produced at the boundary of the inner core is fed into the outer core, moves upward toward the poles, and from there finally flows back inward (Fig. 1).
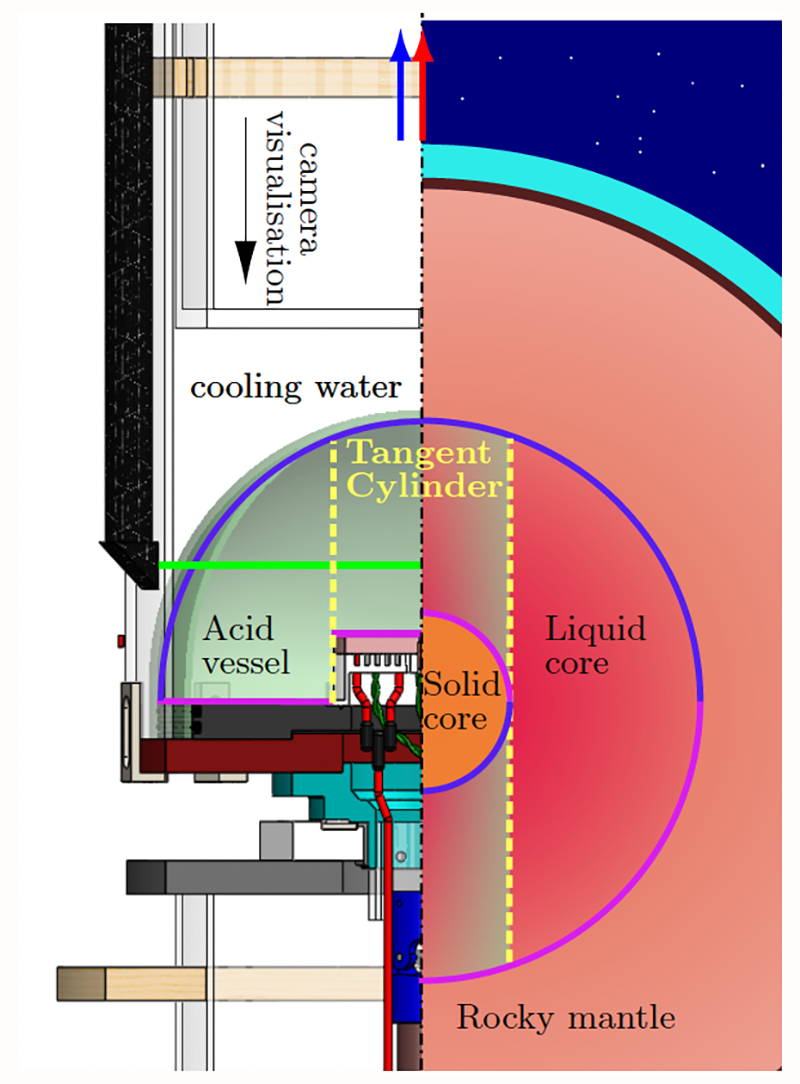
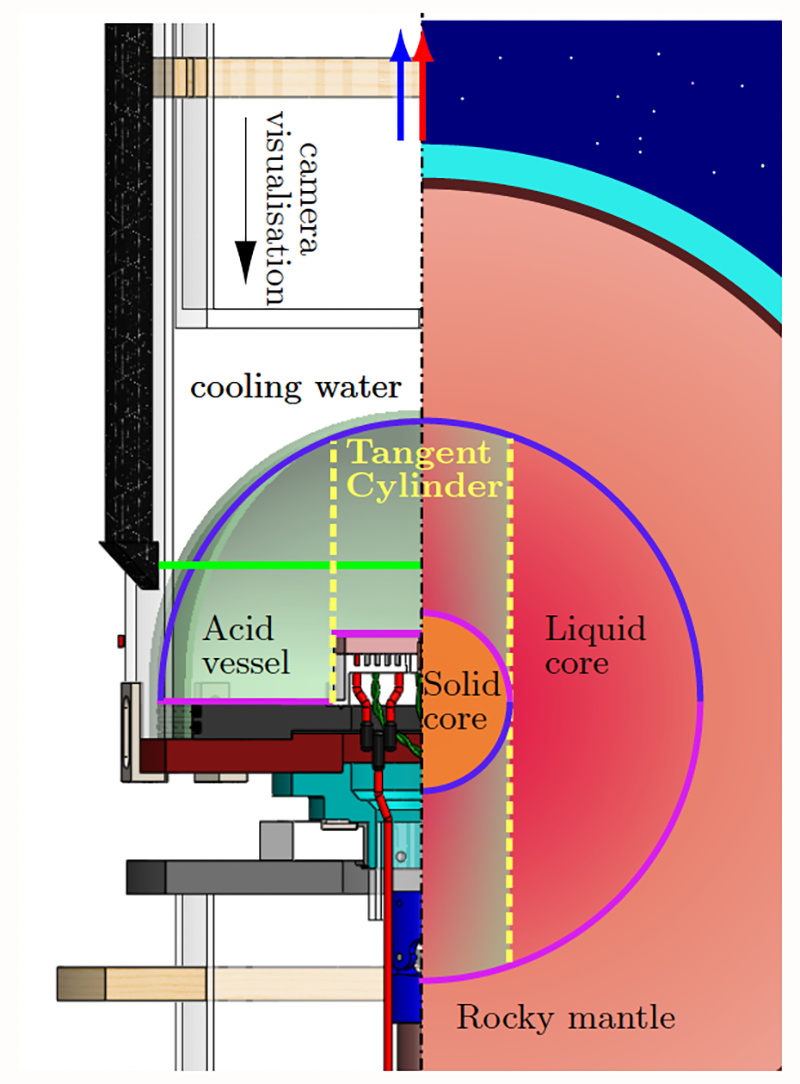
These observations can’t be explained by the established theory for rotating fluids, which assumes that magnetic-field-induced forces on the flow can be neglected, as they are dominated by rotation-induced Coriolis forces. If rotation is fast enough, goes the theory, flows of liquid are two dimensional and lie in the plane normal to the rotation axis. For planetary interiors, this imposes a constraint known as the Taylor-Proudman theorem: Fluid cannot flow across a boundary, called the tangent cylinder, defined by a radial distance equal to the solid-core radius. The flows documented on Earth, however, violate this condition. To explain the discrepancy, what’s needed is an experiment that captures convection, rotation, and magnetism all at once, says Pothérat.
Pothérat and his colleagues have realized such an experiment, using it to vet an extension of the established model associated with the Taylor-Proudman constraint. Previous Earth-mimicking setups used rotating tanks filled with a highly conductive but opaque liquid metal, which prevented the visualization of liquid flows. The team’s “Little Earth Experiment” (Fig. 2) instead used a low-conductivity, transparent sulphuric acid solution, which allowed the acquisition of maps that visualize flow structures in a magnetorotating fluid. “That’s the big originality,” says Pothérat. Since their liquid was much less conducting than a liquid metal, the team needed a large external magnetic field to create magnetic forces sufficiently strong to mimic planet-like conditions. They achieved such conditions using a 10-tesla magnetic field produced by the giant magnet of the Grenoble High Magnetic Field Laboratory in France. “The real feat of our experiment is fitting a rotating tank inside this enormous magnet,” says Pothérat.
The Little Earth Experiment involves a rotating hemispheric dome sitting on a flat, rotating table. The transparent-glass hemisphere was filled with a conductive fluid, which represented the outer core of Earth. At the hemisphere’s flat bottom, a cylindrical heating element protruding into the liquid played the role of Earth’s inner solid core, driving convection. A water-filled, cylindrical plastic tank sat on top of the hemisphere, providing a cooling effect that mimicked that due to Earth’s mantle. By lacing the conductive fluid with hundreds of thousands of micron-diameter hollow glass particles, which scattered incoming laser light, the researchers could track the particles’ positions and measure the fluid’s velocity at multiple points as the tank rotated.
The key measurements were maps of the fluid’s velocity at two heights—one near the solid core and one at latitudes close to the top of the hemisphere—obtained for electromagnetic and rotational forces representative of Earth-like conditions. Fitting such data, the researchers calculated that at least 10% of the liquid flowed in a circulating pattern similar to that occurring in Earth’s core: From the solid core the liquid flowed toward the top of the dome and then toward the equatorial regions. “We can finally see what the flow looks like,” says Pothérat.
The researchers established that the polar component of the magnetic field drives flow between polar and equatorial regions, concluding that this field-induced flow must be taken into account for explaining convective flows that can’t be described by rotation alone. Modifying the conventional theory by adding a magnetic field pointed in the polar direction allowed the researchers to predict exactly when and how much liquid flowed across. The magnetic field fully explains why the flow crosses the tangent-cylinder boundary, says Pothérat.
Hao Cao, a geophysics researcher at the University of California, Los Angeles’s Department of Earth, Planetary, and Space Sciences, calls the work “impressive” and says that the experimental verification of flow regimes “illustrates the critical role of magnetic fields in shaping fluid dynamics in Earth’s and planetary cores.” He adds a cautionary note regarding its direct application to real planetary cores, pointing out that “the fluid dynamics in this experiment has minimal impact on the magnetic field itself.” That’s not the situation expected in planetary cores, he says.
–Rachel Berkowitz
Rachel Berkowitz is a Corresponding Editor for Physics Magazine based in Vancouver, Canada.
References
- A. Pothérat et al., “Magnetic Taylor-Proudman constraint explains flows into the tangent cylinder,” Phys. Rev. Lett. 133, 184101 (2024).