Smooth Control of Active Matter
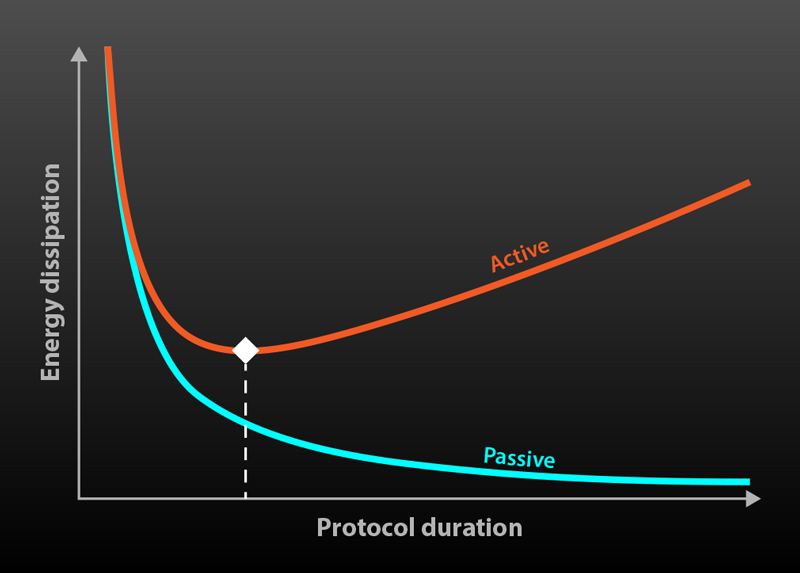
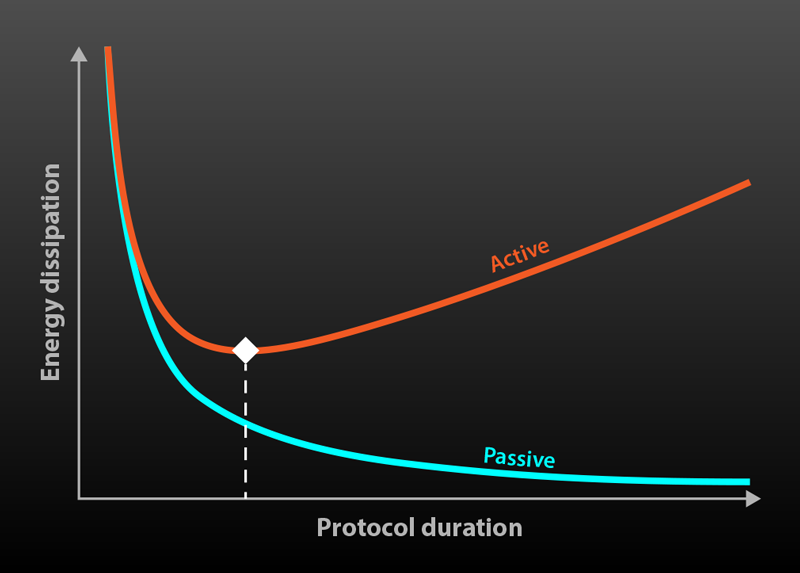
The control of active matter, a class of systems in which each constituent constantly converts energy into directed motion, holds great potential for applications ranging from the targeted delivery of drugs to the creation of smart materials. Using an active-matter system to achieve a particular goal requires that one can efficiently drive it from one state to another. However, active matter’s intrinsic nonequilibrium condition presents a major challenge for theoretical treatments, meaning the most efficient way of driving a system is often difficult to predict. Now Luke Davis at the University of Luxembourg and colleagues have introduced a general framework to determine thermodynamically optimal protocols to drive active systems between different states in a way that minimizes the associated heat dissipation [1]. Their derivation, which applies to the regime of slow, weak driving, offers the key insight that the underlying energy conversion in active systems leads to a trade-off between internal and external dissipation, resulting in the optimal driving process having a finite duration. This is in sharp contrast to passive matter, where quasistatic—that is, infinitely slow—driving is always the most energy efficient.
The search for optimal solutions is an important and centuries-old field of research in mathematics, physics, and engineering. A common goal relevant to biology and the design of machines is finding a process that minimizes heat losses to the environment as the system is driven from one state to another [2–5]. For passive systems, which have historically been the main focus of thermodynamics, these losses go to zero when the system is driven so slowly that it is kept near equilibrium at all times—in the so-called quasistatic limit. To find thermodynamically optimal control strategies that minimize such losses under the constraint of finite-time driving—meaning that the system is driven faster than the quasistatic limit—previous research has developed a versatile geometric approach [2–4] based on response theory, which describes how a system responds to a perturbation.
In this context, the control of active matter poses an interesting yet still largely unexplored challenge, as its underlying nonequilibrium condition enables collective behaviors not seen in passive systems, such as motility-induced phase separation. Active-matter systems also break detailed balance and reciprocity principles, which, in a passive system, require that state transitions show no bias in any direction and that perturbations in opposite directions are symmetrical. The breaking of these principles means that existing control strategies developed for passive systems cannot be straightforwardly applied to active systems.
To generalize thermodynamic control to active matter, Davis and colleagues exploit recent advances in response theory and stochastic thermodynamics [6–8]. As with thermodynamic optimization of passive matter, the team’s approach is based on the assumption that the driving only involves weak and slow changes of a single control parameter. This assumption allows the theoretical treatment to start at the quasistatic limit, where the system is in a steady state at each instant in time; the driving is added as a series of small perturbations to the steady-state behavior. Then, the researchers derive an expression for the average heat dissipation in terms of the correlation functions of the unperturbed dynamics [6–8].
The result is an approximate formula for the average heat dissipation under driving that can readily be evaluated based on steady-state experiments or computer simulations. From this formula, they find a general expression for the optimal driving protocol, and they unravel how the net heat dissipation scales in the limits of long and short protocol duration. From these scalings it follows that the optimal duration has a certain finite value, in contrast to the control of passive matter, where the optimal duration is infinitely long.
This finite value results from a compromise between the dissipation due to external control and the loss due to internal activity (Fig. 1). Minimizing the external-drive dissipation would require a slow, long-duration control process—as in the optimal passive case. But active-matter systems are constantly losing energy to the environment through their internal-drive mechanisms, so reducing that loss entails a fast control process with the shortest duration possible. The employed approach based on response theory is able to capture this trade-off because, at the optimal duration, the control is slower than the relaxation rate of the active matter, so it can still be treated as a small perturbation.
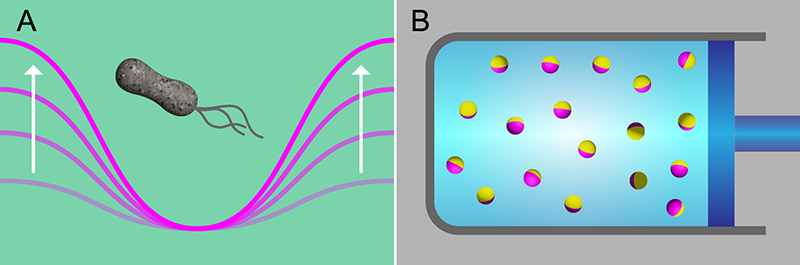
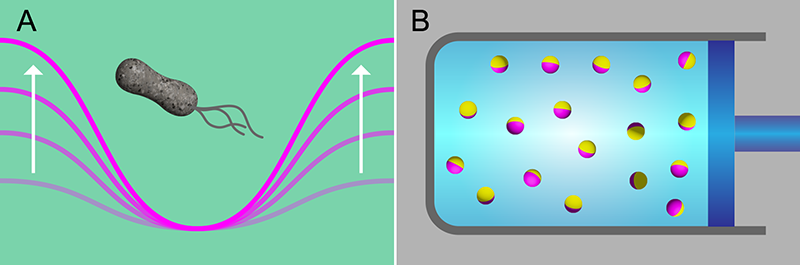
The discovery of the finite optimal protocol duration establishes a feature of minimum-dissipation control that is expected to hold for a broad class of active systems. To demonstrate their framework, Davis and colleagues apply it to specific scenarios. They consider a single active swimmer in a harmonic trap whose stiffness is slowly and weakly changed and a collection of repulsive active swimmers whose packing fraction acts as a control on the collective behavior (Fig. 2). Both examples confirm the general trends and moreover show that the optimal protocols have a richer phenomenology than in the case of passive systems.
Beyond these findings, the framework promises new insights into optimal control of a wide range of active systems. In addition to minimizing the dissipated heat, the framework can also be readily applied, for example, to maximize the extracted work, possibly guiding the design of efficient active heat engines [9] or to inspire new perspectives on microbiological processes. Another interesting application concerns the thermodynamically optimal switching between distinct collective states of active many-body systems, pointing toward the creation of active metamaterials that change their properties on demand.
An obvious drawback of this framework is the underlying assumption of weak and slow driving. This assumption implies a restriction to driving protocols that vary smoothly, limiting the range of applicability. Previous work shows that fast driving ubiquitously leads to nonsmooth optimal protocols, which cannot be treated by the perturbative approach [5]. Therefore, complementary approaches and extensive numerical studies that explicitly tackle the fast-driving regime, possibly supported by machine learning, will be needed to obtain a more complete picture of the optimal control of active matter [10]. Such approaches will be particularly important to the study of collective systems driven across critical points, where the internal relaxation times diverge, or to the construction of microscopic active machines with finite power output [9].
References
- L. K. Davis et al., “Active matter under control: Insights from response theory,” Phys. Rev. X 14, 011012 (2024).
- G. E. Crooks, “Measuring thermodynamic length,” Phys. Rev. Lett. 99, 100602 (2007).
- S. Deffner and M. V. S. Bonança, “Thermodynamic control—An old paradigm with new applications,” Europhys. Lett. 131, 20001 (2020).
- D. A. Sivak and G. E. Crooks, “Thermodynamic metrics and optimal paths,” Phys. Rev. Lett. 108, 190602 (2012).
- T. Schmiedl and U. Seifert, “Optimal finite-time processes in stochastic thermodynamics,” Phys. Rev. Lett. 98, 108301 (2007).
- M. Baiesi et al., “Fluctuations and response of nonequilibrium states,” Phys. Rev. Lett. 103, 010602 (2009).
- S. Dal Cengio et al., “Linear response theory and Green-Kubo relations for active matter,” Phys. Rev. Lett. 123, 238003 (2019).
- E. Lippiello et al., “Nonlinear response and fluctuation-dissipation relations,” Phys. Rev. E 78, 041120 (2008).
- É. Fodor and M. E. Cates, “Active engines: Thermodynamics moves forward,” EPL 134, 10003 (2021).
- M. C. Engel et al., “Optimal control of nonequilibrium systems through automatic differentiation,” Phys. Rev. X 13, 041032 (2023).