Measuring the Information Delivered by Music
Great pieces of music transport the audience on emotional journeys and tell stories through their melodies, harmonies, and rhythms. But can the information contained in a piece, as well as the piece’s effectiveness at communicating it, be quantified? Researchers at the University of Pennsylvania have developed a framework, based on network theory, for carrying out these quantitative assessments. Analyzing a large body of work by Johan Sebastian Bach, they show that the framework could be used to categorize different kinds of compositions on the basis of their information content [1]. The analysis also allowed them to pinpoint certain features in music compositions that facilitate the communication of information to listeners. The researchers say that the framework could lead to new tools for the quantitative analysis of music and other forms of art.
To tackle complex systems such as musical pieces, the team turned to network theory—which offers powerful tools to understand the behavior of discrete, interconnected units, such as individuals during a pandemic or nodes in an electrical power grid. Researchers have previously attempted to analyze the connections between musical notes using network-theory tools. Most of these studies, however, ignore an important aspect of communication: the flawed nature of perception. “Humans are imperfect learners,” says Suman Kulkarni, who led the study. The model developed by the team incorporated this aspect through the description of a fuzzy process through which a listener derives an “inferred” network of notes from the “true” network of the original piece.
The researchers focused on Bach’s work, analyzing hundreds of preludes, fugues, chorales, toccatas, concertos, suites, and cantatas. Bach seemed an ideal starting point for this analysis, as his work has a highly mathematical structure, says Kulkarni. What’s more, Bach’s prolific production allowed comparisons between widely different compositional forms, she says.
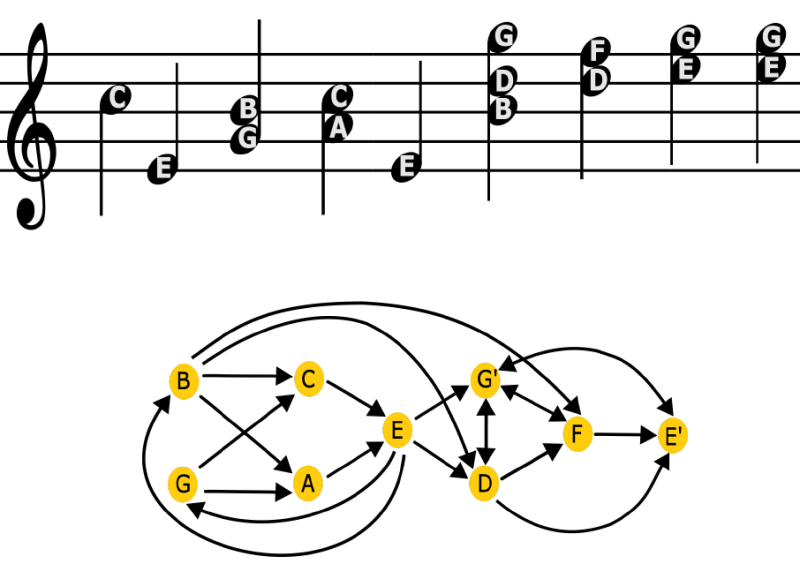
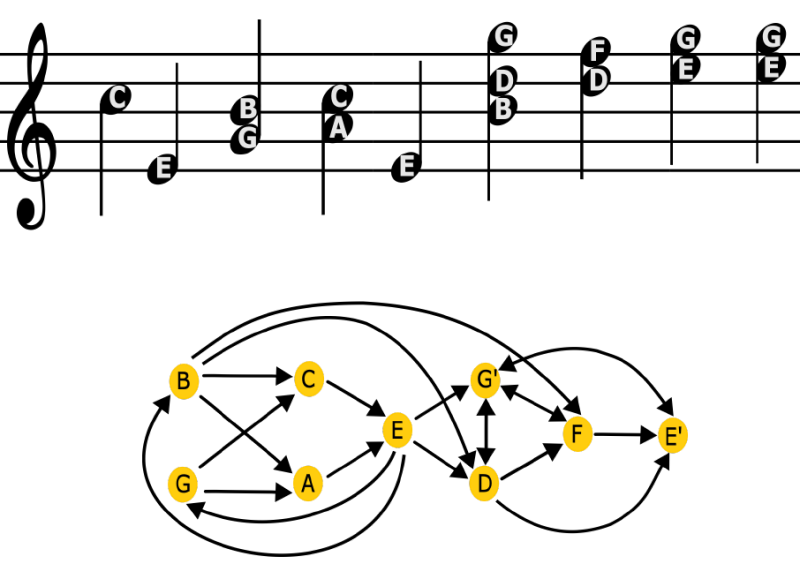
To build a simplified network representation for each of Bach’s pieces, the researchers assigned a node to each note and connected it to other nodes through directed edges representing transitions from each note to the notes played thereafter. They then assigned different “weights,” or thicknesses, to the edges depending on the frequency with which the corresponding note transitions occurred in the piece. For each of the networks derived from the pieces, they quantified the amount of information in the network by computing the “Shannon entropy,” a metric from information theory.
The procedure allowed the researchers to compare different compositional forms, showing that they could be distinguished on the basis of entropy, or information content. For instance, chorales had the lowest entropy, while toccatas and preludes had the highest entropy. Kulkarni says that these differences likely reflect the functions of each form. Chorales—meditative hymns designed to be sung by groups in churches—are simple pieces whose predictability implies low information content, while toccatas and preludes—aimed to entertain and surprise—communicate a wealth of information through their complexity. Examining the entropy of the pieces, the team found that those belonging to the same compositional forms are clearly grouped in clusters with similar entropy.
After building true networks for the analyzed pieces, the researchers computed the inferred networks using a model that describes an average process of human perception. In this process, humans seek a trade-off between accuracy—achieving a sufficiently precise representation of the perceived network—and cost—skipping or simplifying details to reduce the computational complexity of information processing. The team found that, for Bach’s pieces, the differences between true and inferred networks were much smaller than for randomly generated networks—suggesting that music compositions possess features that reduce perception discrepancies. The model allowed the authors to pinpoint some of those features, including certain forms of clustering in the network and the presence of “thick” edges representing note transitions that are frequently repeated.
Kulkarni says that the framework needs to be expanded to incorporate a more realistic description of a musical piece, including elements such as rhythm, timbre (the unique sound quality of a given instrument), counterpoint (the relationship between different melodic lines), and the presence of chords. Such multifaceted aspects of music could be mathematically captured through so-called multilayered networks that are often used in the modeling of multidimensional, real-world networks. She says that an important direction for further work involves a refined description of the perception process, for instance, exploring variability among individuals or considering factors such as musical training and cultural influences.
A more complete representation of the information content in music could allow quantitative comparisons between different pieces. Such an approach could reveal how the music of a specific composer has changed over the course of their lifetime or how compositions have evolved across music traditions, Kulkarni says. She also suggests that the quantitative metrics delivered by the framework could provide feedback to aid composers in their writing process. For example, a music composition software could display measures of entropy and direct the composer toward edits that could either amplify entropy—generating surprise by contradicting musical expectations—or diminish it—through harmonious, easy-to-anticipate resolutions. Kulkarni notes that similar approaches could be applied to other art forms, such as literature, to analyze their information content and learnability. Progress in these fields will depend on exchanges between artists, sociologists, musicologists, and neuroscientists, she says. “There are tall walls between disciplines that complexity science can help tear down.”
–Matteo Rini
Matteo Rini is the Editor of Physics Magazine.
References
- S. Kulkarni et al., “Information content of note transitions in the music of J. S. Bach,” Phys. Rev. Res. 6, 013136 (2024).