Failed Barrier Crossings Tell a Story
A protein molecule sometimes needs to unfold to enter a cell or to begin its degradation. The transition to the unfolded state requires crossing a free-energy barrier, and the protein—driven by thermal fluctuations—must make many attempts to escape its initial metastable folded state. The rare successful attempts have been the focus of previous studies of proteins and similar barrier-crossing systems. New work by Aaron Lyons and colleagues at the University of Alberta, Canada, explores the more common, unsuccessful tries in experiments with optically trapped beads and DNA molecules [1]. Such failed attempts constitute much of the time that each system spends in the metastable state before it escapes, yet each attempt is brief and very difficult to resolve individually. The researchers show that they can probe intriguing questions, such as how far does a system go during an escape attempt before giving up. The answers might offer a mechanistic view of how molecular machines within cells generate mechanical forces and perform other functions.
A remarkably broad family of phenomena can be described as many-body systems escaping from a metastable state. Besides unfolding biomolecules, examples include chemical reactions, nuclear decays, crystal formation, and the spontaneous breaking of large structures such as ships [2]. The rate of escape can be described by the Arrhenius law, which most of us learned about in high school chemistry. The law consists of just two input parameters: a (free-)energy barrier and a prefactor. The former is required to describe how likely it is that the system can be found near the “bottleneck” separating the initial state (for example, folded protein) from the final one (unfolded protein), while the latter is often thought of as the escape-attempt frequency. Scientists typically don’t measure these parameters directly; instead, only the escape rate is usually accessible by experiments. So an open question remains: How does the system escape the initial state?
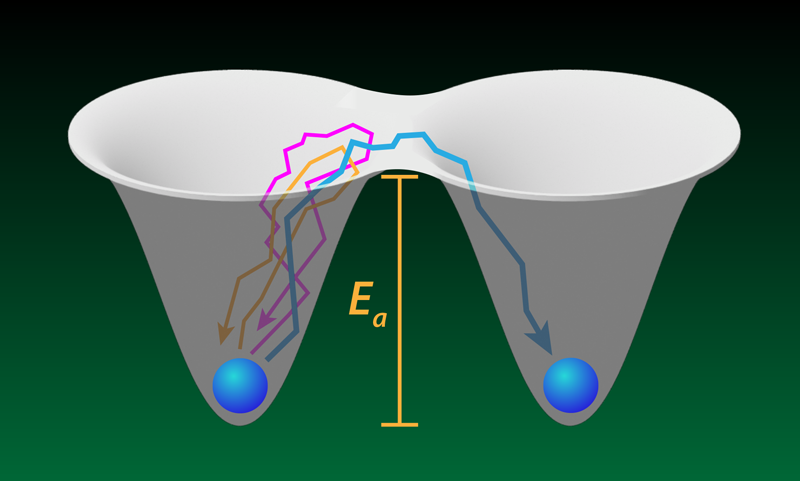
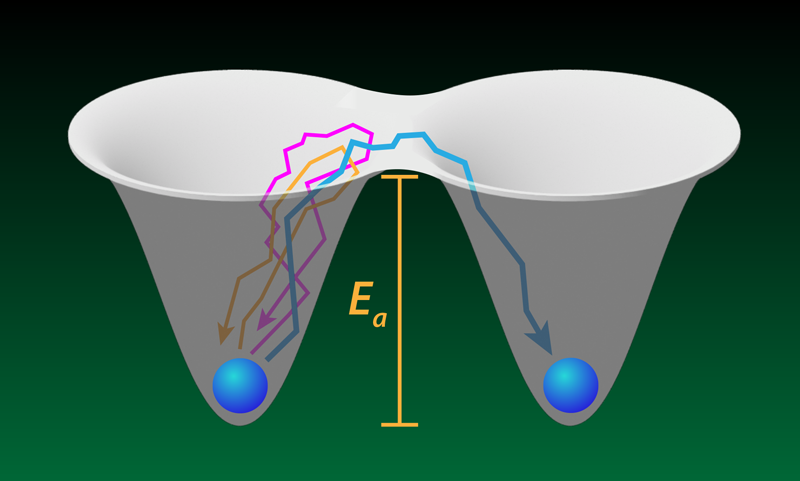
Lyons and colleagues tackle this question with two experiments. The first involved a micron-sized bead held in a pair of optical traps separated by a submicrometer distance. The team measured the position of the bead, tracking its random walks into a barrier region—a “no man’s land” between the two trap centers. Occasionally, the bead hopped from one trap to the other, but more often it failed to escape, entering the barrier region for a few microseconds before falling back into the trap that it started from. The team showed that the statistics of these failed attempts (also called loops [3, 4] or nonproductive fluctuations) matched a simple model where the bead undergoes Brownian motion in a potential created by the two traps.
In a second experiment, the team attached the ends of a DNA molecule, through polymeric handles, to two beads, each located within its own optical trap. When the molecule folds (unfolds), the distance between its ends (that is, the DNA extension x) decreases (increases), resulting in detectable movements of the beads. In failed attempts, x increases or decreases, briefly entering a similarly defined barrier region between the metastable folded and unfolded states, but then returning back to the original metastable basin of attraction (Fig. 1). To capture the dynamics with sufficient time resolution, the researchers increased the stiffness of the optical traps holding the beads. They also took pains to isolate the random walk of the DNA from the random walks of the beads and the polymeric handles.
The DNA extension x used to experimentally monitor the molecule’s progress toward escape is an example of a “reaction coordinate” (using chemistry language) or “order parameter” (using physics parlance). The folding of DNA, however, involves many more degrees of freedom (that is, motions of individual atoms), which are inaccessible to measurements. It is then natural to wonder how much information about the molecule’s transitions between the folded and unfolded states is retained when only its “shadow” (a low-dimensional projection onto the reaction coordinate) can be observed.
To answer this question biophysicists often rely on seminal work from 1940 [5], in which Dutch physicist Hans Kramers proposed a middle ground between fully characterized microscopic dynamics and the phenomenological Arrhenius law. He argued that when x is chosen wisely, its dynamics may be approximated as biased Brownian motion along x, with the effect of the unobserved degrees of freedom amounting to velocity-dependent frictional forces and stochastic noise. Although Kramers originally proposed this model as a description of chemical and nuclear reactions, it turned out to be particularly impactful in numerous subfields of biophysics, where both the enormous complexity of the biomolecular phenomena and the low-dimensional nature of experimental observables call for low-dimensional mechanistic descriptions [6]. At the same time, applicability of the Kramers model has been questioned on theoretical grounds, and it has been suggested that this model would be increasingly inaccurate at timescales significantly shorter than the mean escape time [7].
Since Lyons and colleagues probe microsecond timescales associated with fast excursions into the barrier region, their study offers a critical test of the Kramers model of folding. And indeed, they find that this model still remains applicable to fast folding dynamics. In particular, the team measured the distribution of failed-attempt durations (conditional upon the progress made toward crossing the barrier) and the distribution of turning points (where the system quits the failed attempt), and both observations agreed with the Kramers model to within experimental uncertainties. On the other hand, the strong dependence of the duration of a failed attempt on its spatial extent and the highly nontrivial probability distribution of this duration highlight the fact that the naive interpretation of the Arrhenius prefactor as an “attempt frequency” is generally inadequate.
Going forward, this study opens a new chapter in the exploration of mechanisms of microscopic rearrangements of biomolecules that are responsible for biomolecular function. A particularly useful application of this method would be in the study of molecular machines powering transport of particles across cells and generating forces within cells. Tracking the failed movements of these machines could provide a mechanistic insight into how they convert chemical energy into mechanical work. I further anticipate that other single-molecule techniques, particularly single-molecule fluorescence measurements, will provide additional information on fast biomolecular motions [8, 9]. Fluorescence measurements have the advantage of using less bulky and thus less sluggish probes (that is, dye molecules instead of micron-sized beads), but their time resolution is limited by the rate at which photons can be emitted and detected. Even more exciting would be combining fluorescence experiments with force spectroscopy, which would provide a two-dimensional rather than one-dimensional picture of the dynamics.
References
- A. Lyons et al., “Quantifying the properties of nonproductive attempts at thermally activated energy-barrier crossing through direct observation,” Phys. Rev. X 14, 011017 (2024).
- M. Marder, “Fluctuations and fracture,” Phys. Rev. Lett. 74, 4547 (1995).
- A. M. Berezhkovskii et al., “Exact solutions for distributions of first-passage, direct-transit, and looping times in symmetric cusp potential barriers and wells,” J. Phys. Chem. B 123, 3786 (2019).
- A. M. Berezhkovskii and D. E. Makarov, “On distributions of barrier crossing times as observed in single-molecule studies of biomolecules,” Biophys. Rep. 1, 100029 (2021).
- H. A. Kramers, “Brownian motion in a field of force and the diffusion model of chemical reactions,” Physica 7, 284 (1940).
- A. Szabo et al., “First passage time approach to diffusion controlled reactions,” J. Chem. Phys. 72, 4350 (1980).
- D. E. Makarov, “Barrier crossing dynamics from single-molecule measurements,” J. Phys. Chem. B 125, 2467 (2021).
- H. S. Chung and W. A. Eaton, “Protein folding transition path times from single molecule FRET,” Curr. Opin. Struct. Biol. 48, 30 (2018).
- F. Sturzenegger et al., “Transition path times of coupled folding and binding reveal the formation of an encounter complex,” Nat. Commun. 9, 4708 (2018).