Toward a Second Law for Living Systems
In 1944, Erwin Schrödinger published the book What is life? [1]. Therein, he reasoned about the origin of living systems by using methods of statistical physics. He argued that organisms form ordered states far from thermal equilibrium by minimizing their own disorder. In physical terms, disorder corresponds to positive entropy. Schrödinger thus concluded: “What an organism feeds upon is negative entropy […] freeing itself from all the entropy it cannot help producing while alive.” This statement poses the question of whether the second law of thermodynamics is valid for living systems. Now Benjamin Sorkin at Tel Aviv University, Israel, and colleagues have considered the problem of entropy production in living systems by putting forward a generalization of the second law [2]. Using an information-theoretic framework, they show that their theory can be used to derive important thermodynamic quantities and relations for living systems.
Sorkin and colleagues built upon concepts developed over the past few decades. In the early 1990s, scientists pioneered the study of fluctuation relations, which generalize the second law of thermodynamics to single-particle systems far from thermal equilibrium [3]. In parallel, other researchers laid the foundations of stochastic thermodynamics, which takes fundamental thermodynamic concepts (e.g., heat, work, and entropy) developed for many-particle systems and applies them to stochastic single-particle dynamics [4]. This framework reproduces a whole hierarchy of previously derived fluctuation relations, including the first and second laws of thermodynamics for a randomly moving, or Brownian, particle in a fluid [5].
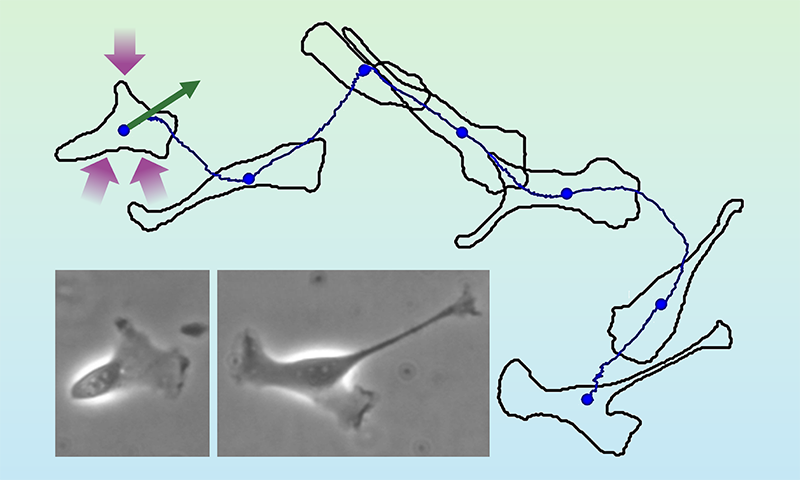
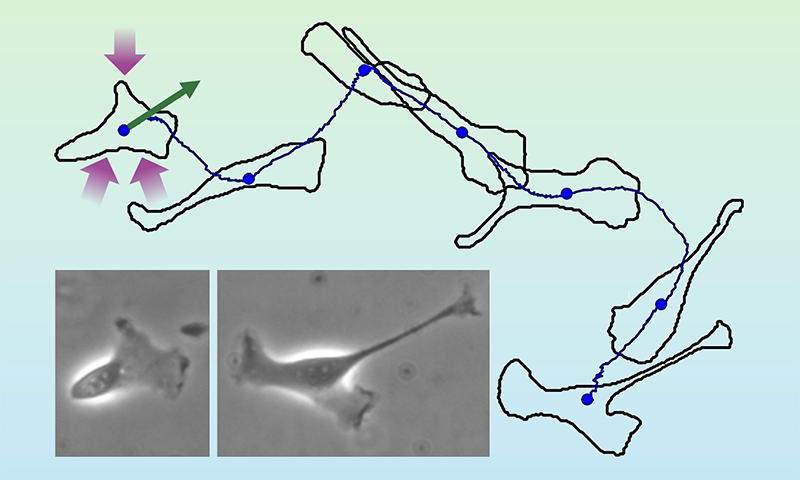
In the past decade, fluctuation relations have been used to describe biological dynamics by linking stochastic thermodynamics with the emerging field of active matter [6]. Examples of active-matter systems range from migrating biological cells to flocks of birds to moving crowds of people [7]. Active motion is self-driven, in stark contrast to the passive dynamics of a Brownian particle. Think of a crawling cell, which propels itself using energy taken up from its environment (Fig. 1). The cell’s path looks random, akin to the trajectory of a Brownian particle in a fluid. But whereas such a particle is passively driven by collisions with surrounding fluid molecules, the cell moves actively by itself.
The dynamics of a Brownian particle is characterized by a balance between the particle’s fluctuations in movement and its dissipative interaction with its environment. Such balance is expressed in terms of the particle’s diffusion coefficient, its mobility, and the temperature of the surrounding fluid. This so-called Einstein relation is an example of a fluctuation–dissipation relation that holds for ordinary classical fluids [3–5]. However, in more complex systems such as polymer gels, the Einstein relation is broken, leading to violations of conventional fluctuation relations [8]. In active matter, the Einstein relation is typically also broken, reflecting the specific uptake of energy and conversion into self-propelled motion [7].
Sorkin and colleagues started from a so-called overdamped Langevin equation, which can be used to model the dynamics of systems without assuming the Einstein relation. Such modeling includes examples of active matter and passive Brownian particles as special cases. By applying stochastic thermodynamics [4, 5], the team rederived the first and second laws of thermodynamics by assuming the existence of an ordinary thermodynamic temperature, as in the Einstein relation.
The researchers then considered a crucial quantity in stochastic thermodynamics known as informatic entropy production, which measures the breaking of time-reversal symmetry on the level of microscopic trajectories. Without assuming the Einstein relation and its corresponding thermodynamic temperature, but by imposing three specific physical conditions, Sorkin and colleagues derived an equation for what they call a generalized nonequilibrium temperature. Using this equation, one obtains a second law without the Einstein relation. If one then assumes this relation, the researchers’ generalized temperature boils down to the ordinary thermodynamic temperature, and their theory recovers corresponding results for conventional stochastic thermodynamics.
An important consequence of the new theory is that, without the Einstein relation and associated thermodynamic temperature, conventional fluctuation relations are recovered only on an abstract, information-theoretic level and not for thermodynamic quantities—in line with previous work [8]. Assuming a generalized temperature, one can derive useful thermodynamic relations such as the Clausius inequality, a generalized “Carnot efficiency,” and bounds between two key quantities—the extractable work and the free-energy change. Sorkin and colleagues suggest that their concept of a generalized temperature could be verified by applying their theory to certain experimental systems in which the Einstein relation is broken.
Achieving the derivation of a new form of the second law that applies to living systems is quite a big claim. Given that the theory does not require the Einstein relation, one might call it a second law of athermal dynamics, where here “athermal” denotes the nonthermodynamic active biological forces that cause deviations from classical thermodynamics [5]. Notably, the theory assumes that the dynamics is both overdamped and Markovian—that is, independent of the system’s history. However, the overdamped approximation, which neglects acceleration and inertia, can fail when fluctuations depend on position, such as for temperature gradients [9]. Moreover, many active biological systems—such as migrating cells—exhibit non-Markovian anomalous diffusion [10]. Along these lines, violations of fluctuation–dissipation relations that are more general than the Einstein relation can come into play [8].
These considerations call for further generalizations of the new theory, as envisioned by Schrödinger [1]: “Living matter, while not eluding the ‘laws of physics’ as established up to date, is likely to involve ‘other laws of physics’ hitherto unknown, which, however, once they have been revealed, will form just as integral a part of this science as the former.”
Acknowledgments
Rainer Klages acknowledges Lennart Dabelow of the Queen Mary University of London for helpful comments on the article.
References
- E. Schrödinger, What is life? (Cambridge University Press, Cambridge, 2012)[Amazon][WorldCat].
- B. Sorkin et al., “Second law of thermodynamics without Einstein relation,” Phys. Rev. Lett. 133, 267101 (2024).
- D. J. Evans et al., Fundamentals of Classical Statistical Thermodynamics: Dissipation, Relaxation, and Fluctuation Theorems: (Wiley, Weinheim, 2016)[Amazon][WorldCat].
- K. Sekimoto, Stochastic Energetics, Lecture Notes in Physics Vol. 799 (Springer, Berlin, 2010)[Amazon][WorldCat].
- U. Seifert, “Stochastic thermodynamics, fluctuation theorems and molecular machines,” Rep. Prog. Phys. 75, 126001 (2012).
- L. Dabelow et al., “Irreversibility in active matter systems: Fluctuation theorem and mutual information,” Phys. Rev. X 9, 021009 (2019).
- S. Ramaswamy, “The mechanics and statistics of active matter,” Annu. Rev. Condens. Matter Phys. 1, 323 (2010).
- S. M. J. Khadem et al., “Stochastic thermodynamics of fractional Brownian motion,” Phys. Rev. Res. 4, 043186 (2022).
- A. Celani et al., “Anomalous thermodynamics at the microscale,” Phys. Rev. Lett. 109, 260603 (2012).
- P. Dieterich et al., “Anomalous dynamics of cell migration,” Proc. Natl. Acad. Sci. U.S.A. 105, 459 (2008).