Repeated Particle Measurements Disagree with Theory—What Now?
The magnetic moment of the muon, which describes how this electron-like particle wobbles in a magnetic field, has been a stubborn nut for particle physicists to crack. The experimentally determined values of this parameter have long disagreed with those from theoretical predictions, a trend that continued with a recent result from the Muon g-2 experiment at Fermi National Accelerator Laboratory in Illinois (see Research News: Mismatch with Standard-Model Predictions Reaches 5 Sigma). Such a discrepancy is exciting, as it could provide a hint of new physics that might resolve some of the outstanding problems in particle physics. However, the size of the discrepancy depends on which group of theorists you talk to. Resolving that theoretical discrepancy is currently the top goal for researchers in the muon-moment community.
“On the theory side, we have a lot of work to do,” says Aida El-Khadra from the University of Illinois at Urbana-Champaign. She is the chair of the Muon g-2 Theory Initiative—a collective of theorists and experimentalists working to determine what value the standard model of particle physics predicts for the muon’s magnetic moment. A few years back, the initiative seemed to be closing in on a single number [1]. But in 2021 a rift opened between the predictions of two separate methods for calculating the muon’s moment, leaving theorists without a clear prediction. “The ball is in our court, and we are working hard to get it back over the net,” El-Khadra says.
For the past two years, theorists have been busy refining their calculations, but the rift remains. “There’s still a real disagreement between the approaches,” says initiative member Thomas Blum from the University of Connecticut. Using computer simulations and experimental data, physicists are homing in on the origin of the discrepancy, and they hope that these efforts will provide a resolution. Then, perhaps they can go back to pondering the experiment–theory discrepancy and its implication for the standard model, El-Khadra says. “The mood is very cautious. But the possibility of new physics is still alive.”
Lost in a Virtual Haze
If the muon were a classical object, its moment would equal 2 (in dimensionless units). But it is not. The measured value is about 0.1% more than 2. That tiny extra bit—the muon’s so-called anomalous magnetic moment (aµ)—arises from interactions of the muon with particles that briefly pop in and out of existence. These “virtual” particles form a haze around the muon, influencing how it responds to a magnetic field.
Virtual particles come in all varieties: electrons, neutrinos, vector bosons, and everything in between. But the ones that give theorists the biggest headache are the hadrons, which are quark-containing particles such as pions and protons. “This is the source of all the difficulties,” El-Khadra says.
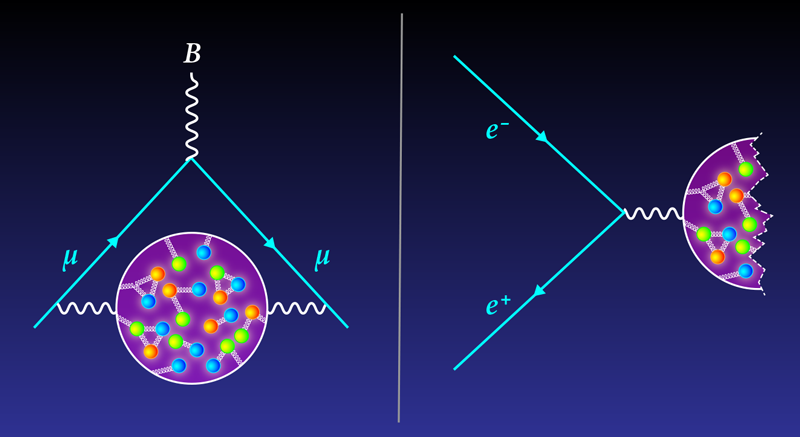
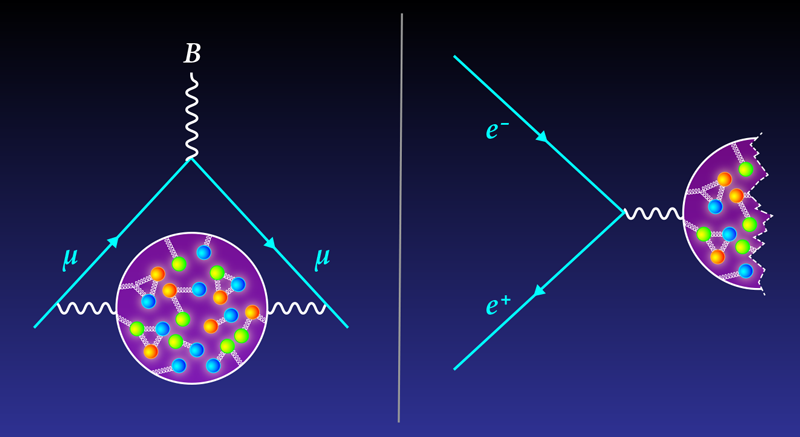
Calculating the net effect of virtual hadrons on the muon’s magnetic moment—the so-called hadronic vacuum polarization (HVP)—to high precision is a daunting task, so theorists use tricks. In the “data-driven” approach, the trick involves using experimental data from electron–positron collisions to estimate the HVP. Specifically, researchers select the fraction of such collisions that produce hadrons. Because electrons and muons are from the same particle family, the probability of producing real hadrons in electron–positron collisions is related to the haze-like influence of “virtual” hadrons on the muon moment.
The theoretical conversion of electron–positron collision data into an estimate of the HVP is a “straightforward business,” says experimentalist Michel Davier from the University of Paris-Saclay. Less straightforward is collecting the needed data from the experiments. This limitation may seem surprising, as there have been many electron–positron collider experiments over the years, including BaBar in the US and KLOE in Italy. But a lot of these experiments were designed to study high-energy collisions (10 GeV and more), whereas computing the HVP requires low-energy collisions (less than about 2 GeV).
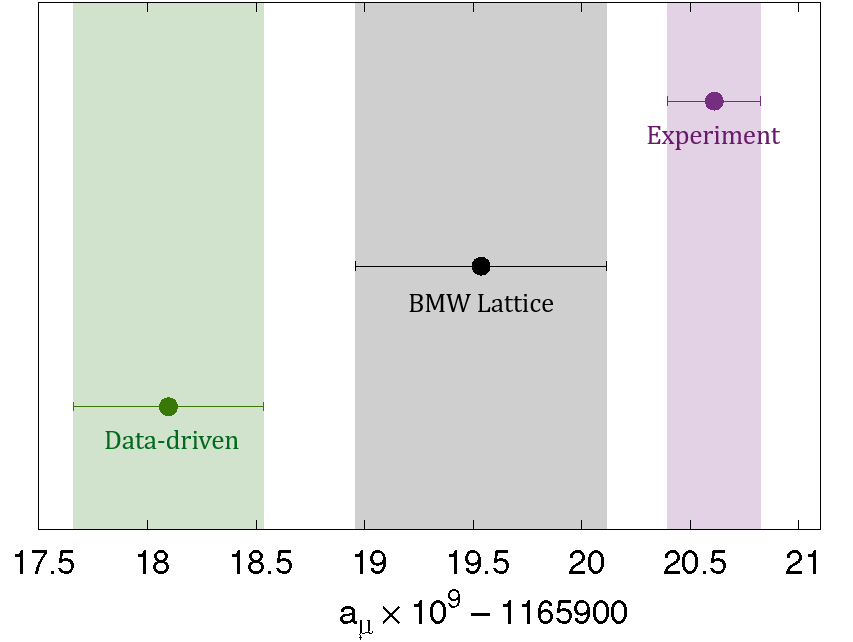
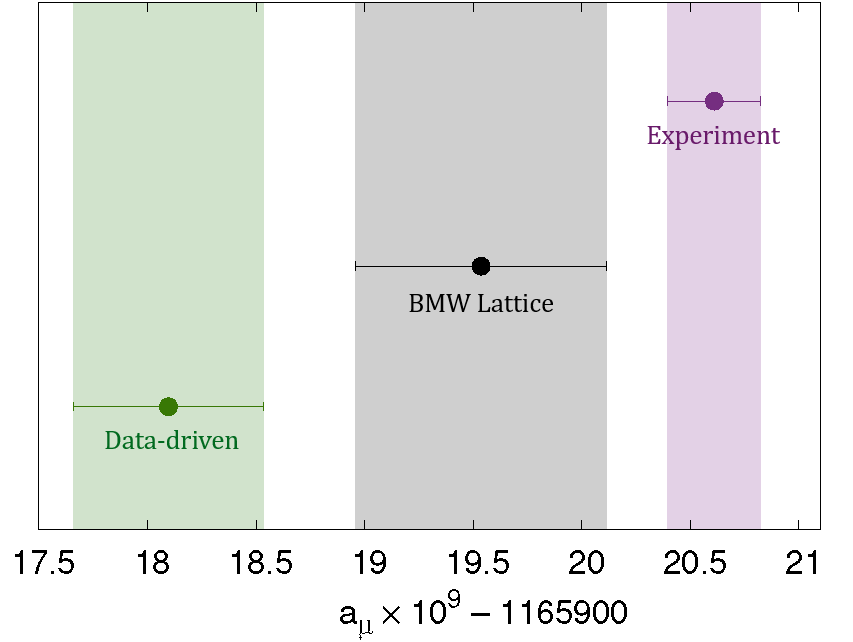
Physicists have navigated this energy problem by targeting rare low-energy events that occur when either the electron or the positron emits a photon before the collision. Davier and his colleagues used this technique to extract low-energy data from BaBar measurements, and others have done similar extractions from KLOE measurements. The HVP estimates made using the different data don’t match, so in 2020 the Muon g-2 Theory Initiative compiled the estimates to determine an average data-driven HVP value with an uncertainty (error bars) of around 0.6%. Combining this value with other computations, the initiative came up with an anomalous magnetic moment prediction of aµ = 0.00116591810, with a precision of 0.4 parts per million (ppm) that is limited primarily by the uncertainty in the HVP contribution. This theoretical value lies 2.1 ppm below the most recent estimate from the Muon g-2 measurement [2].
Clinging to the Lattice
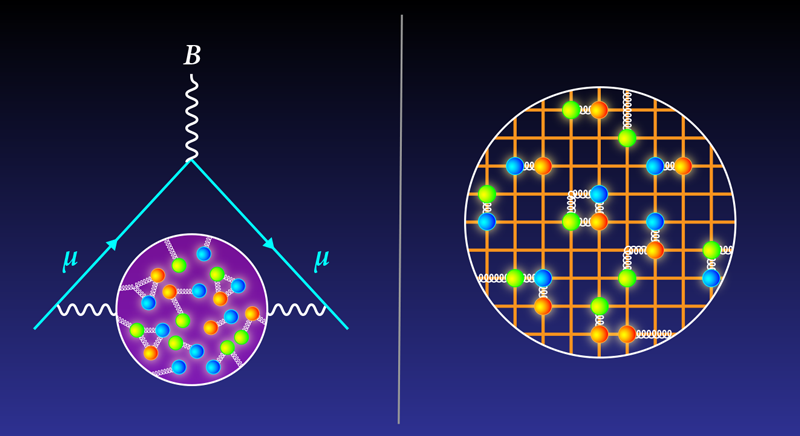
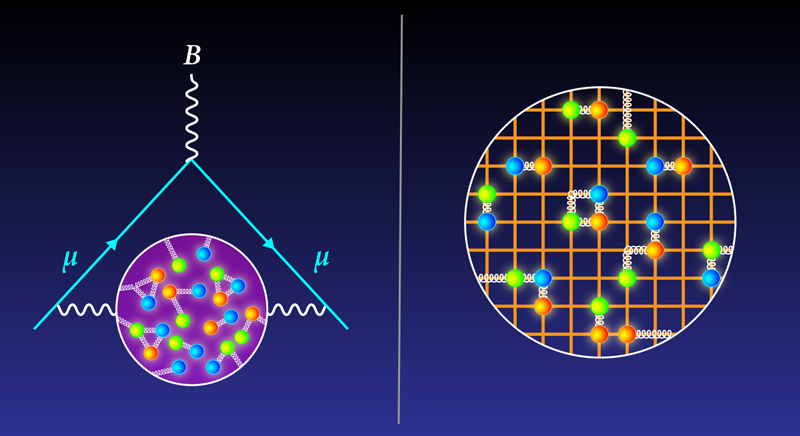
The data-driven approach has been the go-to method for HVP calculations for two decades. But in the past few years, another method, the lattice approach, has become a viable alternative. The trick for this method is to discretize space-time when calculating the interaction of a muon with the virtual haze. “It’s a first-principles approach with no experimental input,” Blum says.
The basis of the lattice approach is quantum chromodynamics, a theory that describes the interactions among quarks and gluons (the strong-force carriers). Quantum chromodynamics calculations are notoriously difficult, but physicists have made progress in making them more manageable by assuming that particles move in a stepwise fashion on a lattice, like pieces on a chessboard. This discretization of space allows difficult mathematical integrals to be broken down into more manageable sums.
For a given lattice configuration, researchers perform multiple simulations, emulating an experiment being run multiple times. They then take an average of these simulations to arrive at an estimate of physical quantities such as the mass and spin of certain particles (see Viewpoint: Dissecting the Mass of the Proton).
The difficulty with the lattice approach is that discretizing space-time introduces uncertainties that depend on the distance between lattice sites and on the lattice’s overall dimensions. Researchers typically use site separations of about a tenth of a femtometer and boxes that are several femtometers per side (1 femtometer equals 10−15 m, which is roughly the width of a nucleus). Calculations of the HVP value under those conditions typically have error bars around 3% percent, larger than those of the data-driven results.
That situation changed in 2021 when the Budapest-Marseille-Wuppertal (BMW) Collaboration released an HVP value with error bars of 0.8% [3]. “This was the first time that the lattice approach actually became competitive with the data-driven approach,” says BMW team member Laurent Lellouch from Aix-Marseille University, France. The collaboration performed a large number of lattice simulations, allowing them to reduce the statistical and systematic uncertainties in their calculations. The effort took several years and hundreds of millions of processor hours on large supercomputers. “There was a lot of ‘elbow grease’ involved,” Lellouch says.
When combined with other computations, the HVP value from BMW corresponds to an anomalous magnetic moment of aµ = 0.00116591954, which is larger than the data-driven prediction by about 1.2 ppm. The BMW lattice prediction is closer to the experimental value than the data-driven one, having a discrepancy of 0.9 ppm.
A Window into the Problem
The disagreement of the BMW result with the data-driven one threw doubt upon theoretical understanding of the muon’s magnetic moment. But particle physicists have been hesitant to accept it without more evidence. “The BMW result is an impressive calculation, but it is the only one at the sub-1% precision level,” El-Khadra says. She says that the community is waiting for other equally precise results from other lattice groups that use different discretization techniques and error-reducing methods. Lellouch agrees that cross-checks are important. But such studies will take time: three years on, no other lattice group has yet released an HVP computation with the sub-1% precision achieved by the BMW Collaboration.
While these time-consuming cross-checks continue, several groups have been working on quicker computations that could provide a preliminary test of whether lattice groups are on the same track. Blum and his colleagues showed that they could divide the HVP calculation into three parts using the distance over which the muon interacts with virtual hadrons. They then focused on the middle part, or “intermediate window,” which Blum says is quicker and easier to calculate than the full HVP [4].
The intermediate window is also less dependent on the details of a particular lattice simulation, such as the magnitude of the site separations and the methods for the error corrections. That makes the intermediate-window HVP calculations “a lot less sensitive to all of the ways in which the calculations can go wrong,” El-Khadra says.
Currently, there are eight independent lattice-method calculations of the intermediate-window HVP value, and they all agree. But they disagree with an estimate of the intermediate-window quantity computed within the data-driven approach. In fact, the difference between the lattice and data-driven window values is greater—in terms of statistical significance—than the difference between the full HVP estimates from the lattice and data-driven approaches. Blum calls the window difference a “serious discrepancy,” as it suggests that the lattice and data-driven approaches diverge in this intermediate region where the uncertainties were thought to be the smallest.
Small Earthquake
While the past two years have seen increased agreement in the lattice camp, disagreement has surfaced in the data-driven one. In February 2023, the CMD-3 Collaboration in Russia reported data on electron–positron collisions from the VEPP-2000 collider, which operates at energies below 2 GeV and so is directly relevant to HVP computations [5]. The CMD-3 results disagree with observations from the BaBar and KLOE experiments, as well as with measurements from CMD-2 (a previous generation of CMD-3) and from SND (another ongoing experiment at the VEPP-2000 collider). “The report caused a small earthquake,” El-Khadra says.
The new CMD-3 results are based on more than 30 million hadron-producing events—many times more than those from previous experiments. “Right now, the CMD-3 result has the highest statistical precision,” says CMD-3 team member Fedor Ignatov from the University of Liverpool in the UK. He says the disagreement between the results from CMD-3 and previous experiments is significant, reaching as high as 5% with KLOE.
The origin of this disagreement is currently unknown. “We can only speculate at this moment,” Ignatov says. The CMD-3 Collaboration has investigated the possibility that the disagreement comes from detector effects, and they are considering an equipment upgrade that might address this issue. Another possible culprit is the so-called Monte Carlo methods used to analyze collision data. Davier and his colleagues recently reported a possible problem with one of the more commonly used Monte Carlo methods, which might partly explain the disagreements between electron–positron collision results [6].
To put the data-driven approach on more solid ground, researchers are intensifying efforts to analyze archived data. Davier has initiated an investigation of unanalyzed data taken with BaBar, which stopped operating 10 years ago. Ignatov is a part of a similar effort that is using archived data from the also-finished KLOE experiment. There are also ongoing electron–positron experiments at the Beijing Spectrometer III in China and Belle-II in Japan, but their results are not expected for several years. The analysis of the BaBar data should come out later this year, and that of the KLOE data will likely follow a year or two after. “Maybe some clarifications will appear in 1–3 years from now,” Ignatov says.
On the lattice side, Blum says that his group is working on completing a full calculation of the HVP with the same sub-1% precision achieved by the BMW Collaboration. He expects to release results in the first half of this year. El-Khadra say that her lattice group will also release a full HVP lattice calculation this year. “The lattice community is marching on,” Blum says.
So what does the future hold for new physics? For now, no one wants to speculate. But both Blum and El-Khadra note that if the final theoretical prediction ends up being close to the current lattice estimates, there would still be a discrepancy with experimental values. And no matter what happens, theorists will have to explain why their two main calculation methods gave such different answers. “I’m by no means pessimistic,” Blum says. “There’s going to be something very interesting to discover.”
Correction (16 January 2024): A previous version of the story mentioned that the BMW lattice simulations reported in 2021 only reduced statistical uncertainty. The calculations instead reduced both systematic and statistical uncertainties.
–Michael Schirber
Michael Schirber is a Corresponding Editor for Physics Magazine based in Lyon, France.
References
- T. Aoyama et al., The anomalous magnetic moment of the muon in the Standard Model, arXiv:2006.04822.
- D. P. Aguillard et al. (Muon g – 2 Collaboration), “Measurement of the positive muon anomalous magnetic moment to 0.20 ppm,” Phys. Rev. Lett. 131, 161802 (2023).
- S. Borsanyi et al., “Leading hadronic contribution to the muon magnetic moment from lattice QCD,” Nature 593 (2021).
- T. Blum et al. (RBC and UKQCD Collaborations), “Update of Euclidean windows of the hadronic vacuum polarization,” Phys. Rev. D 108 (2023).
- F. V. Ignatov et al. (CMD-3 Collaboration), “Measurement of the e+e− → 𝜋+𝜋− cross section from threshold to 1.2 GeV with the CMD-3 detector,” arXiv:2302.08834.
- J. P. Lees et al. (BABAR Collaboration), “Measurement of additional radiation in the initial-state-radiation processes e+e− → 𝜇+𝜇−𝛾 and e+e− → 𝜋+𝜋−𝛾 at BABAR,” Phys. Rev. D 108, L111103 (2023).
- B. Abi et al., “Measurement of the positive muon anomalous magnetic moment to 0.46 ppm,” Phys. Rev. Lett. 126, 141801 (2021).