Time-Symmetric Motion Maximizes Energy Efficiency in Fluid
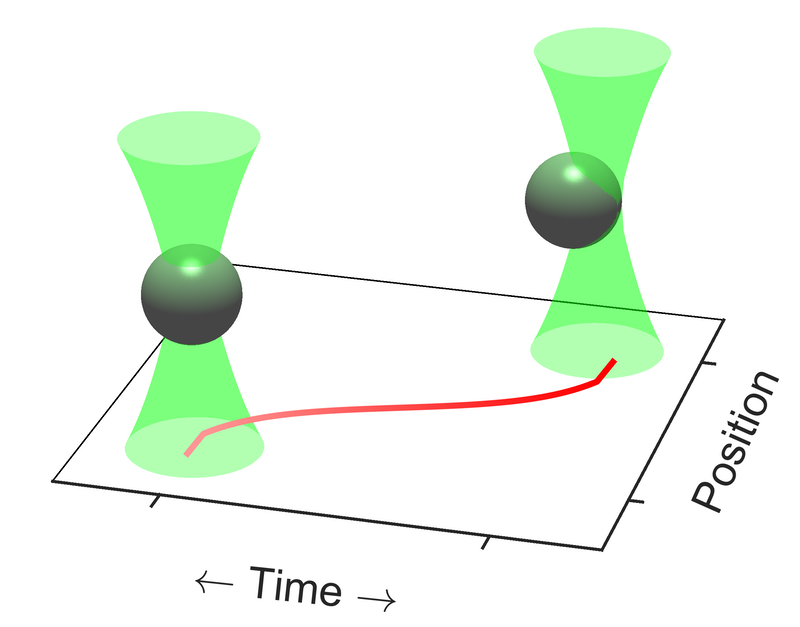
A research team has demonstrated that the most efficient protocol for dragging a microscopic object through a fluid has an unexpected feature: the variation of the velocity with time after the midpoint of the trip is the reverse of its variation up to the midpoint [1]. This time-symmetry property, the researchers say, can help to identify the most efficient control strategy in a wide variety of micromechanical systems and could improve the operation of tiny machines.
Biomedical engineers are exploring micro- and nanoscale devices that swim through the body under their own power to deliver drugs [2]. Machine-like motion at tiny scales is also common in biology, for instance in the transport of compartments called vesicles by motor proteins inside cells [3]. To understand the energetics of such systems, Sarah Loos of the University of Cambridge and colleagues have studied a simple model of microscale transport. They used optical tweezers—a laser beam that can trap a small particle—to drag a 2.7-micrometer-diameter silica sphere through fluids. “This problem is simple enough to be solved analytically and realized experimentally, yet rich enough to show some fundamental characteristics of optimal control in complex systems,” says Loos. In practice, the device inducing the motion “could be a nanorobot carrying a drug molecule or a molecular motor that pulls or pushes against a microscopic object.”
The researchers studied two types of fluid: a viscous solution of glycerol and a solution containing soap-like surfactants that give the fluid viscoelastic properties, like the springiness of honey or saliva. Whereas viscous fluids simply create a frictional drag on a moving particle, viscoelastic fluids can briefly store energy when deformed.
In the experiments, the researchers didn’t actually move the microparticle but held it in the optical tweezers and moved the fluid cell in which it was suspended. The particle was also free to move within the trap, and Loos and her colleagues monitored this motion. They tested various protocols for taking the particle along a straight path between two points. Each protocol consisted of varying the cell’s speed (in effect, the trap’s speed) in a different way. Based on these measurements, the team calculated the work exerted on the particle for each protocol; the most efficient protocol was that for which this work was smallest.
For viscous fluids, the best strategy was one where the particle jumps abruptly into motion and then moves at a constant speed to its destination. For a viscoelastic fluid, the optimal way to vary the speed was more complex, slowing the particle in mid-flight to reduce the elastic energy that builds up in the fluid. However, in both cases, the best scheme was time-symmetric, both for the relative velocity of the optical trap and for the actual motion of the particle within it. The team showed theoretically that the same principle should also apply to many other kinds of fluids.
This result isn’t obvious, given that moving the particle is itself a nonequilibrium process in which the end state is very different from the starting one. For example, dragging the particle through a viscous fluid will stir the fluid and cause energy to be lost, rather like dragging a spoon through coffee to stir in the cream.
Loos and colleagues showed that this time-symmetry property could be used as an optimization criterion by a machine-learning algorithm. They compared the results of two algorithms, one tasked with finding the protocol that does the least work on the particle and one instructed to find the protocol that came closest to time symmetry for the trap and particle motion. They found that both algorithms converged on the same solution.
The researchers’ analysis only works for particles trapped in a harmonic potential—as if held by an ideal spring, for which the “centering” force is proportional to the displacement. But this requirement, says Loos, still encompasses a large class of situations because such forces can often be approximated as harmonic. Whether the criterion of time-symmetry is used by biological systems remains to be seen, she adds, because in living systems, energy efficiency might not always be the top priority.
“The authors provide an elegant argument for the time-reversal symmetric protocol,” says David Sivak, a statistical physicist at Simon Fraser University in Canada. “I find the theoretical result surprising, and surprisingly general, and there is impressive agreement with experiment.” Sivak hopes it will be possible to extend the analysis to cyclical motions, where the object returns to its starting point—a common situation for any engine.
–Philip Ball
Philip Ball is a freelance science writer in London. His latest book is How Life Works (Picador, 2024).
References
- S. A. M. Loos et al., “Universal symmetry of optimal control at the microscale,” Phys. Rev. X 14, 021032 (2024).
- R. Nauber et al., “Medical microrobots in reproductive medicine from the bench to the clinic,” Nat. Commun. 14 (2023).
- J. E. Rothman, “The machinery and principles of vesicle transport in the cell,” Nat. Med. 8 (2002).