Classifying the Surface Magnetization of Antiferromagnets

Sai Mu

Viewpoint

Classifying the Surface Magnetization of Antiferromagnets

University of South Carolina, Columbia, SC, US

May 28, 2024• Physics 17, 88

Group theory and first-principles calculations combine to predict which antiferromagnets have potentially useful net surface magnetization.

Figure caption — **Figure 1:** The four categories of surface magnetization on surfaces that have roughness, or steps. Robustness arises when the surface moments (magenta) on either side of the step point in the same direction. Magnetism is induced when the moments reorient themselves at the surface.

Antiferromagnetism was discovered in the 1930s by Louis Néel but had long been considered of scientific, not practical, interest. Antiferromagnets (AFM) are internally magnetic, but the magnetic moments of their atoms and molecules are antiparallel to each other, canceling out and resulting in no net magnetization. This cancellation renders bulk antiferromagnets effectively invisible to external magnetic fields, so that their magnetic properties are difficult to harness in applications. Recently, however, a new paradigm has appeared—antiferromagnetism-based spintronics—which seeks to apply antiferromagnets’ unique properties (such as fast spin dynamics, the absence of strong stray fields, and the stability of these materials) to the processing and storage of information [1]. Despite the internal cancellation of magnetic moments in bulk antiferromagnets, surface magnetization can exist, as revealed by experimental and theoretical studies, offering new potential use in antiferromagnetic spintronics. What’s been missing is a comprehensive, unified theory to predict and explain surface magnetization of AFM. Now, Sophie Weber of the Swiss Federal Institute of Technology (ETH) in Zurich and her collaborators have applied group theory and density-functional theory to derive a universal classification system that accounts for the observed surface magnetization of antiferromagnets based on their inherent magnetic symmetries [2]. These new developments bode well for the development of a broad class of AFM-based devices that could be game changers for information processing.

Magnetic properties of materials are often determined by their internal, bulk magnetic symmetry [3]. But at the surface, this symmetry, and with it, the material’s properties, change. This transformation is particularly interesting in antiferromagnets, whose surface effects are less understood than those of their ferromagnetic counterparts. Almost three decades ago, Alexander Andreev introduced a phenomenological model that suggested antiferromagnets could exhibit finite surface magnetization [4]. Later, Kirill Belashchenko used an elegant symmetry analysis to argue that certain antiferromagnets could possess equilibrium surface magnetizations, provided they are also magnetoelectric (ME)—that is, their magnetic and electric properties are coupled such that their magnetization can be controlled by an electric field and their polarization can be controlled by a magnetic field [5]. The ME effect was first formulated by Lev Landau and Evgeny Lifshitz in one of their famous textbooks [6]. Later, Igor Dzyaloshinskii identified the antiferromagnet ${Cr}_{2} O_{3}$ as the first intrinsic ME material [7].

Intuitively, on a surface with roughness or steps, there are nearly equal amounts of magnetic atoms with opposite moments. On average they cancel out, giving zero (or tiny) surface magnetization. Belashchenko pointed out that the magnetization of ME ${Cr}_{2} O_{3}$ on its (001) surface is both finite and insensitive to surface roughness—predictions that were confirmed experimentally in 2010 [8, 9]. In layered structures combining ${Cr}_{2} O_{3}$ layered with ferromagnets, the experimenters also found an exchange bias—that is, a shift in the hysteresis loop [8]. The exchange bias was electrically reversible, indicating the possibility of electrical control of the surface magnetization.

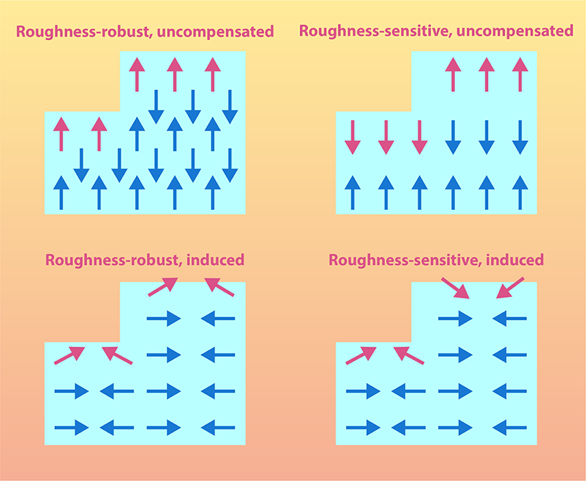
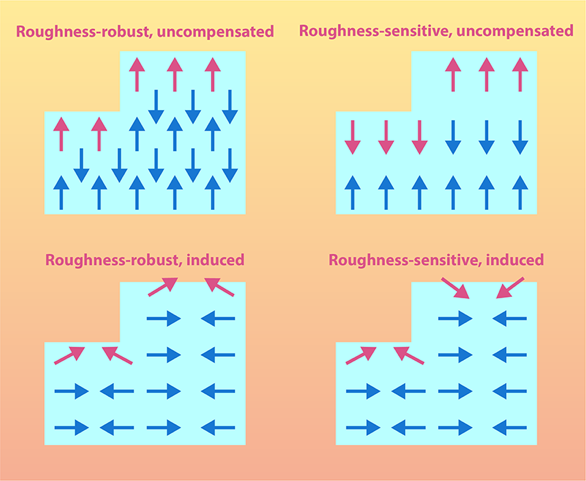
Weber and her collaborators set out to develop a comprehensive and unifying classification system that could account for the magnetization on a general surface of AFM materials, not just ${Cr}_{2} O_{3}$ . Sketched in Fig. 1, the system they model determines how the surface magnetization is affected by the surface’s roughness and whether it arises naturally from the material’s internal structure or is induced by the reduction in symmetry at the surface.

Building on Andreev’s and Belashchenko’s seminal work, Weber and her collaborators used an extended group-theory approach to identify which surface planes of a given AFM show surface magnetization, differentiating between those that are affected by surface roughness and those that are not. To validate their approach and assess its accuracy, they calculated the surface magnetization of various surfaces of AFM materials, such as ${Fe}_{2} O_{3}$ , ${Cr}_{2} O_{3}$ , and ${FeF}_{2}$ using density-functional theory.

They also showed that surface magnetization can be described by considering three ME multipoles—that is, the monopole, toroidal moment, and quadrupole, which make up the magnetoelectric tensor. ME multipoles could therefore serve as the key bulk-order parameters for the surface magnetizations. Conversely, the existence of surface magnetization may imply hidden ME multipoles.

Remarkably, the research of Weber and her collaborators reveals that even surfaces with a typical in-plane AFM magnetic moment alignment and whose magnetism would otherwise be cancelled out, or compensated, can unexpectedly display symmetry-induced magnetization. This phenomenon, driven from a surface-symmetry-induced interaction known as the Dzyaloshinskii–Moriya interaction, was newly predicted by some of the same authors to be both sizable and stable at the (100) surface and ( $\bar{1} 20$ ) surface of ${Cr}_{2} O_{3}$ [10]. This unexpected result, also supported by experiments [11, 12], is a breakthrough, as it widens the possibilities for searching and utilizing surface magnetization of AFM materials. Surfaces of AFM that were thought to be compensated are now in play for spintronic applications.

The newly developed group-theory formalism offers a practical method and flowchart for identifying specific surfaces of antiferromagnets that have surface magnetization, delineating how their surface magnetization arises, and determining how they are affected by the surface’s roughness. Easily combined with data-driven methods, the formalism is particularly useful for researchers looking to design materials that leverage surface magnetism for technological applications, such as data storage and information processing with logic gates. The surface magnetization observed might also be linked to the mechanisms behind exchange bias and spin-splitting, even without external magnetic fields. These insights could lead to new ways to manipulate antiferromagnetic domains without applying a magnetic field. Applications in data storage and processing could result, notably, in all-electric magnetic random-access memories and better giant-magnetoresistance read heads.

References

V. Baltz et al., “Antiferromagnetic spintronics,” Rev. Mod. Phys. 90, 015005 (2018).
S. F. Weber et al., “Surface magnetization in antiferromagnets: Classification, example materials, and relation to magnetoelectric responses,” Phys. Rev. X 14, 021033 (2024).
S. Borovik-Romanov and H. Grimmer, International Tables for Crystallography, Vol. D (Springer, Dordrecht, 2006), p. 105.
A. F. Andreev, “Macroscopic magnetic fields of antiferromagnets,” Jetp Lett. 63, 758 (1996).
K. D. Belashchenko, “Equilibrium magnetization at the boundary of a magnetoelectric antiferromagnet,” Phys. Rev. Lett. 105, 147204 (2010).
L. D. Landau and E. M. Lifshitz, Electrodynamics of Continuous Media (Pergamon Press, London, 1960)[Amazon][WorldCat].
I. E. Dzyaloshinskii, “On the magneto-electrical effect in antiferromagnets,” Sov. Phys. JETP 10, 628 (1960).
X. He et al., “Robust isothermal electric control of exchange bias at room temperature,” Nature Mater. 9, 579 (2010).
N. Wu et al., “Imaging and control of surface magnetization domains in a magnetoelectric antiferromagnet,” Phys. Rev. Lett. 106, 087202 (2011).
O. V. Pylypovskyi et al., “Surface-symmetry-driven Dzyaloshinskii-Moriya interaction and canted ferrimagnetism in collinear magnetoelectric antiferromagnet ${Cr}_{2} O_{3}$ ,” Phys. Rev. Lett. 132, 226702 (2024).
T. Lino et al., “Resistive detection of the Néel temperature of $C r_{2} O_{3}$ thin films,” Appl. Phys. Lett. 114, 022402 (2019).
K. Du et al., “Topological surface magnetism and Néel vector control in a magnetoelectric antiferromagnet,” npj Quantum Mater. 8, 17 (2023).

About the Author

Sai Mu is an assistant professor at the University of South Carolina, with broad interests in emergent phenomena in magnetic quantum materials, disorder physics, defect physics in wide bandgap semiconductors, and quantum information science. He received his PhD from the University of Nebraska-Lincoln, focusing on the first-principles study of magnetoelectric antiferromagnets for spintronic applications. After postdoctoral positions at Oak Ridge National Laboratory and the University of California, Santa Barbara, he joined the University of South Carolina in 2022.