Drug-Resistance Mutations Find Strength in Small Numbers
During the past 50 years, researchers have accumulated a massive arsenal in our war on cancer. Well over 500 drugs have been approved to treat tumors, but cancer remains the second leading cause of death in the United States. The problem is partly due to drug resistance—the emergence of treatment-resistant mutants of the original disease. Now a study led by Jeff Maltas of Cleveland Clinic and Case Western Reserve University, both in Ohio, puts forward a model explaining why drug resistance is so common, vetting the model with experiments on lung cancer cells [1]. This model indicates that treatment-resistant mutants can be present in larger-than-expected numbers before treatment begins. The conclusion implies that we cannot understand cancer evolution by looking at individual mutations in isolation; instead, we should consider each tumor as an interacting ecosystem. The result could be applicable to many diseases that involve evolutionary processes, such as bacterial and viral infections.
Drug resistance is not just a cancer issue. Antibiotics, antifungals, antiparasitics, herbicides, pesticides, and even some vaccines can fail in a similar manner [2, 3]. After initial success in killing off the target cells or organisms, the treatment can be rendered ineffective by the emergence of a resistant subpopulation. Strategies for preventing, slowing down, or overcoming drug resistance have received a lot of attention. Studies that view the emergence of resistant mutants through the lens of evolution play a major role in this effort because they can answer important questions, such as whether resistance emerges before or during treatment. What’s more, these evolutionary models can help design treatment protocols that combine delivery of different drugs with recovery periods to optimize the therapeutic effect.
A major weakness of evolutionary modeling is that it relies on many assumptions on an extremely complex process. The “survival-of-the-fittest” principle is not sufficient for reliable predictions. One would need to know the rate of various mutations, the effects of each mutation on resistance, and other technical details such as the variance in the number of offspring. It is impractical or even impossible to measure all these variables to feed them into the simulations. Instead, scientists make the simplest possible assumptions, compute their consequences, compare predictions to experimental data, and finally go back to refine the initial assumptions to reconcile eventual disagreements.
This situation has led to a major incongruence between theory and experiments, which Maltas and colleagues have worked to resolve. On the one hand, drug resistance is very common. In fact, many tumors contain a resistant mutant before the onset of treatment [4]. On the other hand, theory predicts that resistant mutants should be exceedingly rare. Experiments have repeatedly shown that such mutants have an evolutionary disadvantage: unless the drug is present, they incur a heavy penalty in growth rate and therefore should be outcompeted by their ancestor [5]. Clearly, we need to refine some assumptions. But which ones?
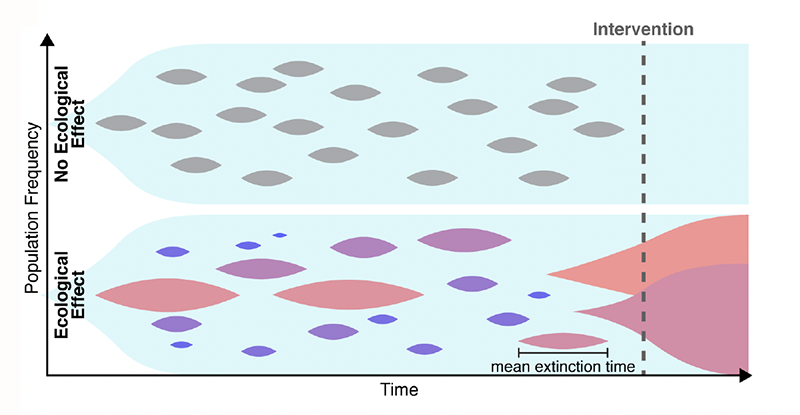
Many explanations have been put forward to solve this conundrum. For example, the estimates of the mutation rate may be too low. One might also need to account for the spatial aspects of disease growth, which can make natural selection less efficient [6]. Maltas and colleagues have now found another possible explanation, in a place where few people were looking. The researchers hypothesized that the growth-rate penalties for resistant mutants depend on the context (Fig. 1). Namely, a resistant mutant, when cultured in isolation, grows much slower than its ancestor. By contrast, when the mutant and its ancestor are cultured together, the growth-rate penalty becomes weaker. Specifically, the penalty decreases in proportion to the relative abundance of the ancestor, and the penalty nearly vanishes when the mutant is very rare. Thus, a small subpopulation carrying a resistance mutation would not experience a strong purifying selection and should persist for a long time, leading to resistance to a later-applied drug.
To test this hypothesis, the first step the team took was to translate the qualitative argument described above into a rigorous mathematical model. The idea that the evolutionary fitness of a mutation—its ability to leave offspring—can depend on the mutation’s relative abundance, or “frequency,” is not new. But such frequency-dependent selection had not been studied in the context of mutation accumulation. Maltas and colleagues generalized several classic results in population genetics to account for the possibility that the fitness cost increases as the mutant becomes more abundant. Their analytical model showed that even when frequency-dependent mutations are very rare, they should constitute most mutations present in the tumor because their lifetimes are so much greater than those of frequency-independent mutations. Through numerical simulations, the researchers validated their analytical results—confirming that frequency-dependent mutations could explain high levels of drug resistance.
The next, most compelling testing step involved experiments validating the frequency-dependent model. The researchers took a lung-cancer cell line as an ancestor and engineered three mutant cell lines by inserting commonly observed drug-resistance mutations. All three mutants grew slower than the ancestor when cultured separately, but the growth-rate penalty nearly vanished when the mutants were cultured together with the ancestor. As an additional test, the researchers cultured two of the mutants without the ancestor and found that this condition didn’t cause any increase in the growth rate. (This observation further supports the team’s conclusions because one does not expect any increase in frequency-dependent interactions between strains that are not adjacent in an evolutionary trajectory, that is, they differ from each other by more than one mutation.)
Maltas and colleagues have built a strong case for frequency-dependent selection as an important mechanism of drug resistance. Their results are also supported by recent observations of similar dynamics in microbial populations during the evolution of antibiotic resistance [7]. Collectively, these works suggest that it is time to move beyond the simple paradigm that mutations confer a fixed change in the growth rate. Instead, we should consider how mutations alter ecological interactions, which in turn affect the growth dynamics.
The new work might have important practical applications in treating cancer by refining evolutionary models of drug resistance with the inclusion of frequency-dependent selection. The results also motivate further research aimed at shedding light on the molecular mechanisms underpinning the benefit that a mutant derives from its ancestor. If scientists could develop drugs able to cut off that benefit, the resistant mutants would be outcompeted through evolutionary selection, and the subsequent treatment could be much more effective.
References
- J. Maltas et al., “Frequency-dependent ecological interactions increase the prevalence, and shape the distribution, of preexisting drug resistance,” PRX Life 2, 023010 (2024).
- N. Sabtu et al., “Antibiotic resistance: What, why, where, when and how?” Br. Med. Bull. 336, ldv041 (2015).
- W. F. Carman, “Vaccine-induced escape mutant of hepatitis B virus,” The Lancet 336, 325 (1990).
- L. A. Diaz Jr et al., “The molecular evolution of acquired resistance to targeted EGFR blockade in colorectal cancers,” Nature 486, 537 (2012).
- A. H. Melnyk et al., “The fitness costs of antibiotic resistance mutations,” Evol. Appl. 8, 273 (2014).
- M. O. Lavrentovich et al., “Spatially constrained growth enhances conversional meltdown,” Biophys. J. 110, 2800 (2016).
- T. Dimitriu et al., “Negative frequency dependent selection on plasmid carriage and low fitness costs maintain extended spectrum 𝛽-lactamases in Escherichia coli,” Sci. Rep. 9, 17211 (2019); A. M. Leale and R. Kassen, “The emergence, maintenance, and demise of diversity in a spatially variable antibiotic regime,” Evol. Lett. 2, 134 (2018).