Preparing Entangled States Efficiently
Initializing a quantum computer for a task involves more than simply pushing the power button. For many situations, it requires the creation of a specific initial state of entangled quantum bits (qubits)—a taxing computational step. Kevin Smith at Yale University and Brookhaven National Laboratory in New York, Abid Khan at the University of Illinois Urbana-Champaign, and their colleagues have now proposed a way to more efficiently perform this task, compared with previous solutions, for initial configurations called matrix product states [1]. The resulting performance improvement could help move quantum computers toward uses in many-body problems in fields such as condensed-matter physics and quantum chemistry.
Matrix product states are relatively simple configurations in which the qubits are weakly entangled. But preparing a many-qubit quantum computer in such a state can be challenging. The problem is that as the number of qubits grows, the number of sequential quantum operations required to reach the state—a measure known as the circuit depth—increases. Since every operation potentially introduces noise into the process, larger systems are beyond the capability of the noisy quantum devices currently available.
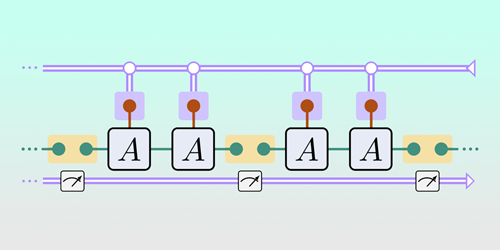
Smith, Khan, and their colleagues get around this problem by breaking the state-preparation process into chunks, which they solve in parallel and subsequently stitch together using what they call adaptive quantum circuits. This approach involves making measurements partway through the process and using the results to guide the subsequent operations. The upshot is that the required circuit depth stays constant even as the matrix product state grows. Last year the team used a similar method to prepare the simplest possible matrix product state on IBM’s quantum processor [2], but the new proposal should allow the preparation of a broad class of such states.
–Marric Stephens
Marric Stephens is a Corresponding Editor for Physics Magazine based in Bristol, UK.
References
- K. C. Smith et al., “Constant-depth preparation of matrix product states with adaptive quantum circuits,” PRX Quantum 5, 030344 (2024).
- K. C. Smith et al., “Deterministic constant-depth preparation of the AKLT state on a quantum processor using fusion measurements,” PRX Quantum 4, 020315 (2023).