A 21st century Rutherford experiment

Illustration: Adapted from Lemasson et al. [4].

Illustration: Adapted from Lemasson et al. [4].

×

In 1909, Hans Geiger and Ernest Marsden [1] reported on the strange behavior of $\alpha$ particles scattered by a gold foil. They observed a wide angular distribution that could not be explained by Thompson’s picture of an atom consisting of “a number $N$ of negatively charged corpuscles, accompanied by an equal number of positive electricity uniformly distributed throughout a sphere” [2]. Ernest Rutherford explained these observations by proposing a small positively charged nucleus in the center of the atom, drawing the first conclusions on the structure of the atomic nucleus [3]. On the basis of this assumption he developed a formula that precisely describes the elastic scattering in ion-ion collisions and set the starting point for a long history of reaction mechanism studies.

Now, $100$ years after the scattering experiments of Geiger and Marsden, Antoine Lemasson and colleagues from France, India, Poland, and the US report in Physical Review Letters on a very similar approach. They used the extremely neutron rich and unstable ${}^8\text{He}$ in comparison with ${}^4\text{He}$ ( $\alpha$ particles) and ${}^6\text{He}$ as projectiles to study collisions on ${}^{197}\text{Au}$ at energies around the Coulomb barrier [4]. However, the focus of the work at the SPIRAL accelerator facility at the GANIL laboratory in Caen, France, is not elastic Rutherford scattering, but fusion and the transfer of neutrons from the light projectile to the heavy target. Just as researchers did at the beginning of the last century, Lemasson et al. obtain new information on the reaction mechanism guiding those collisions and determining the tunneling through the repulsive barrier between the colliding nuclei. And, like Rutherford, they are able to draw conclusions on the importance of nuclear structure in the reaction process, in particular, for the neutron configuration of the very-neutron-rich ${}^8\text{He}$.

An effort to understand the structure of neutron-rich helium isotopes by means of transfer reactions was carried out in Dubna [5] with a low-energy ${}^6\text{He}$ beam on a helium target. In this measurement, an enhancement of the transfer cross section at backward scattering angles was observed, which could only be attributed to the transfer of a pair of neutrons. These observations were confirmed by calculations using the Fermionic Molecular Dynamics model [6] with the Argonne $\text{V}18$ interaction. It is interesting to note that both ${}^5\text{He}$ and ${}^7\text{He}$ have unpaired neutrons and are unbound. The dineutron is also unbound, so all subsystems in a three-body representation (e.g., ${}^6\text{He}=\alpha +$ $\text{n}+$ $\text{n}$) fall apart, which has a mechanical analogy in the so-called Borromean rings in the coat of arms of an aristocratic family of that name in Italy. Removal of any one of the rings (or nuclear parts) causes the entire structure to disintegrate. Hence, the ${}^6\text{He}$ and ${}^8\text{He}$ nuclei are referred to as Borromean systems.

${}^5\text{He}$ represents the case of an almost pure single-particle state bound to an $\alpha$ core as the main configuration. Approaching the neutron drip-line (where the binding energy becomes zero) throughout the isotopic chain, one would essentially expect more and more neutrons in the same shell to be added to the $\alpha$ core, in order to assemble the heaviest helium isotopes. Assuming this simple picture, a theoretical study [7] has been carried out which leads to spatial configurations that also show, in particular, two dineutron pairs around the $\alpha$ core. However, it can be shown that in the case of ${}^7\text{He}$, for example [8], this simplistic picture is not valid, and a more complicated structure has to be assumed. Very different reactions at all accessible energies have been studied in many laboratories (see, e.g., the review article by Jonson [9]) around the world in order to unveil the intrinsic structure of ${}^8\text{He}$. The experiment of Lemasson et al. [4] adds another piece of valuable information due to its particular sensitivity to the spatial neutron configuration.

Nuclear fusion is a process with many facets in modern nuclear physics. It is a possible source for energy production in light-ion collisions. It is the driving force in stellar evolution and the major process to extend the periodic table to ever higher atomic numbers on the way towards the long-sought island of stability in the region of the heaviest chemical elements. In heavy-ion collisions close to and below the Coulomb barrier, fusion competes with processes like Rutherford’s elastic scattering, and with inelastic excitation of and nucleon transfer between the reaction partners. Of particular interest is the regime at sub-barrier energies where fusion is classically forbidden and where it can proceed only via quantum tunneling. In that region in particular, the competing processes couple via mutual interaction [10]. This has direct consequences for the fusion probability as a function of bombarding energy, which in return yields a sensitive tool to study the structure of the reaction partners and the reaction dynamics [11].

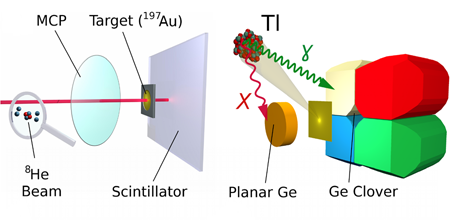
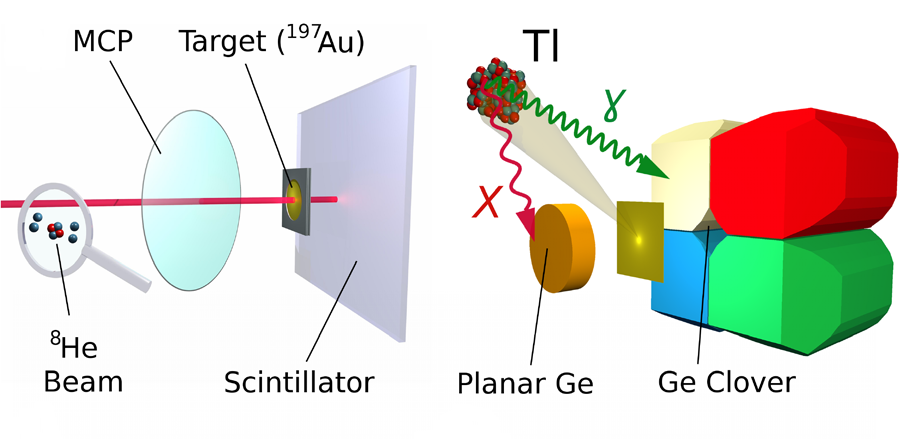
At the SPIRAL accelerator, ${}^8\text{He}$ (with a half-life of $119.1$ ms) is produced in the fragmentation of a $75-$ $\text{MeV/nucleon}$ ${}^{13}\text{C}$ beam. The resulting neutron-rich nuclei are reaccelerated in a radioactive ion beam (RIB), but due to the very low intensity of $4\times {10}^5$ particles per second, special experimental techniques are required to improve the sensitivity of the method. To identify the reaction products, which are ${}^{199,200,201,202}\text{Tl}$ for fusion and ${}^{198,198\text{m},199}\text{Au}$ for neutron transfer, and to measure their half lives, Lemasson et al. employed a novel method that measured $\gamma$ rays with and without coincident detection of x rays [12] (see Fig. 1). The cross-section values measured at various bombarding energies around the Coulomb barrier are then used in comparison with model calculations that take the mutual couplings of the reaction channels into account. The He isotopic series with the two “Borromean” nuclei, ${}^{6,8}\text{He}$, offers special features, like the smaller charge radius of the heavier ${}^8\text{He}$ [13] and a nucleon emission threshold that varies from $20.5\text{MeV}$ to $0.9\text{MeV}$, which then result in an unusual tunneling behavior observed by Lemasson et al. The addition of the neutron pair for ${}^8\text{He}$, as compared to ${}^6\text{He}$, does not increase the probability of fusion. For a loosely bound, but essentially isotropic system like ${}^8\text{He}$, it turns out to be easier to transfer part of the neutron excess to the target than to readjust the outer skin of the system, tunnel as a whole and fuse. While comparing the ${}^8\text{He}$ fusion excitation function with earlier data for ${}^6\text{He}$ and ${}^4\text{He}$, Lemasson et al. obtain a complete and comprehensive picture for the fusion process from the very-well-bound $\alpha$ particle to loosely bound systems with the extreme neutron-rich ${}^8\text{He}$ as projectiles. In this way, they clarify the rather unusual tunneling behavior and the importance of the intrinsic structure of a composite many-body quantum system and pairing correlations.

With the rare isotope facilities planned and/or under construction worldwide, exotic beams—and in particular neutron-rich species—will become available at higher intensities. Reaching farther out to more and more exotic nuclei, studies like the ones discussed here will reveal hitherto unknown features of nuclear matter, manifested in an unexpected distribution of nucleons within a nucleus and other exotic structure phenomena. Such new findings have the potential to clarify and change our picture of the atomic nucleus, with consequences for many fields, such as nuclear astrophysics, hadron and particle physics, and atomic physics.

About the Authors

Dieter Ackermann received his Ph.D. in 1995 from the Technical University Darmstadt, Germany, for his work on sub-barrier heavy-ion fusion. After a postdoctoral appointment at the Argonne National Laboratory (1995–1996), he held a staff scientist position at the LNL accelerator laboratories in Legnaro, Italy, from 1997 to 1999. Since early 1999 he has been a member of the superheavy element research group at the GSI Helmholtzzentrum für Schwerionenforschung in Darmstadt, Germany. The focus of his activities is reaction mechanism studies in heavy-ion collision, structure of very heavy and superheavy nuclei, and the synthesis of new elements.

Haik Simon received his Ph.D. in 1998 from the Technical University Darmstadt, Germany, where he studied the nuclear structure of light exotic ions. After a postdoctoral appointment at CERN (1998–2000), he returned to TU Darmstadt as a scientist, and in 2003 became a member of the nuclear reaction and astrophysics research group at the GSI Helmholtzzentrum für Schwerionenforschung in Darmstadt. His main research activities include studies with light exotic systems at and beyond the drip-line, and the planning of an electron-ion collider experiment (ELISe) at the Facility for Antiproton and Ion Research (FAIR).

Related Articles

Astrophysics

Seeking Supernovae in Seafloor Sediments

December 17, 2024

Minerals exposed during an ancient Mediterranean Sea desiccation should reveal damage caused by muons, providing evidence of enhanced cosmic-ray fluxes. Read More »

Nuclear Physics

A Toroidal Mode in an Excited Nucleus

December 4, 2024

Nuclear scattering data suggest the possible observation of a predicted but never-observed nuclear vibration. Read More »

Nuclear Physics

A Route Toward the Island of Stability

October 21, 2024

Scientists have synthesized an isotope of the superheavy element livermorium using a novel fusion reaction. The result paves the way for the discovery of new chemical elements. Read More »

More Articles