Are black holes really two dimensional?

Vijay Balasubramanian

Viewpoint

Are black holes really two dimensional?

Department of Physics, University of Pennsylvania, Philadelphia, PA 19104, USA

December 7, 2009• Physics 2, 102

The insights of a provocative connection between general relativity and quantum field theory, called the AdS/CFT correspondence, have been extended to rotating black holes that can occur astrophysically.

Figure caption — **Figure 1:** (Left) Black hole spacetimes develop a “throat” leading to the horizon. (Right) The throat viewed from above. Quantum gravitational dynamics in some black hole throats can be “holographically” encoded in the dynamics of a lower dimensional field theory defined on the boundary of the throat. The radial direction of spacetime becomes an emergent geometric description of RG scale in the field theory. Red shading on the boundary indicates the nonlocal spread of data about a local bulk object in the boundary encoding. The depth of red shading indicates the fraction of information about the bulk object that is encoded at each boundary location.

General relativity makes the dramatic prediction that a sufficiently dense cloud of matter collapses to a black hole—a spacetime singularity surrounded by a horizon. A classical observer can enter a large horizon with no ill effects, but the causal structure of a black hole spacetime is such that she cannot return from beyond. Black holes have a mass $(M)$ , they can carry electrical or magnetic charge $(Q)$ , and can rotate (with angular momentum $J$ ). But beyond these characteristics, they “have no hair,” i.e., they have no other distinguishing classical characteristics. To be gravitationally stable, the mass of a charged or rotating black hole must exceed a so-called extremal bound, e.g., rotating black holes, also known as Kerr black holes [1], satisfy the relation $G M^{2} \geq | J |$ . Long a staple of science fiction, there is now a significant body of evidence that black holes, or at least objects very like them, exist in our universe at the centers of galaxies and as endpoints of stellar collapse.

One of the most curious properties of black holes is the enormous entropy that they carry. Gedanken experiments carried out since the early 1970s [2,3] have established that a black hole of horizon area $A$ should respond to probes as if it were a thermodynamic object with an entropy $S = A / 4 G_{N} ħ$ , where $G_{N}$ is the Newton constant and $ħ$ is Planck’s constant. (Here we have adopted units in which we set the speed of light and Boltzmann’s constant to $1$ ). Thus a solar mass black hole (about 6 kilometers wide) should have an entropy that is 22 orders of magnitude greater than the entropy of the sun itself. We have known since Boltzmann, that entropy in a physical system is a manifestation of statistical degeneracy of the underlying states. Following Boltzmann then, a central question for a quantum theory of gravity is to explain how black holes contrive to have an underlying statistical degeneracy of $e^{A / 4 G_{N} ħ}$ . Since the area of an astrophysical black hole grows as the mass squared, this is a truly staggering degeneracy. Measured by an apparatus with energy resolution $Δ E$ , this implies a microstate level spacing proportional to $Δ M \sim Δ E e^{- A / 4 G_{N} ħ}$ . It has been argued [4] that the difficulty of resolving such minuscule differences in the $ħ \to 0$ limit is the source of the apparent semiclassical paradox [5] of loss of quantum unitarity in black holes. Thus a key challenge to any quantum theory of gravity is to identify the “atoms of spacetime” that can explain such a spectacular growth in the number of microstates.

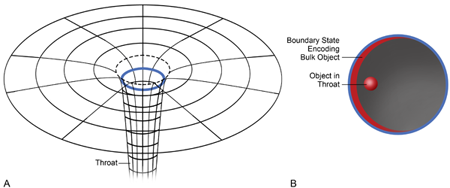
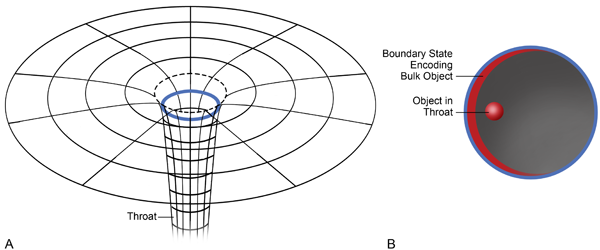
For a special class of highly symmetric, near-extremal charged black holes, this problem was solved in string theory by Strominger and Vafa [6]. With hindsight, we now know that a key ingredient in their solution was that the physics of near-extremal black holes is largely controlled by properties of the spacetime in the vicinity of, but outside, the black hole horizon. Within this so-called black hole “throat” (see Fig. 1, left) the geometry takes a universal form—it is an anti-de Sitter (AdS) spacetime, namely the same geometry as a solution to Einstein’s equations with a negative cosmological constant. In a celebrated paper, Maldacena argued that quantum gravity in every such spacetime is equivalent or “holographically dual” to a nongravitating, conformally invariant, quantum field theory (CFT) in a lower number of dimensions [7] (Fig. 1, right).

This idea, the AdS/CFT correspondence, has some analogy to optical holograms, where the image of a three-dimensional object can be stored nonlocally in a two-dimensional piece of film and then recreated with coherent light. In the context of the AdS/CFT correspondence, spacetime itself is an emergent phenomenon, simply a convenient rewriting of the immensely complicated, strongly coupled physics of a conventional local quantum field theory defined on the boundary of spacetime (Fig. 1, right). The radial direction of spacetime appears as a geometric realization of the renormalization group scale of the field theory [8]. A black hole in anti-de Sitter spacetime is then simply described in the holographic dual theory as a thermal state (a gas with a temperature), whose statistical degeneracy explains the black hole entropy. The AdS/CFT correspondence has been such a powerful and productive tool, that for about a decade the bulk of the effort to understand spacetime singularities and horizons has revolved around black holes in anti-de Sitter spacetimes, at least amongst string theorists.

However, we do not live in a world with a negative cosmological constant, nor are astrophysical black holes highly electrically or magnetically charged as in the examples of Strominger and Vafa. How then do we apply the insights of the last decade to black holes in our universe? In a paper in Physical Review D, Guica et al. [9] point out that near-extreme rotating black holes certainly occur in nature (GRS 1915+105, with mass about 14 times the mass of the sun has $J / G_{N} M^{2} > 0.98$ ), and propose that the dynamics controlling the statistical degeneracy and low-energy emission from such black holes is described “holographically” by a nongravitating, two-dimensional, conformal theory.

The argument does not involve string theory, or any other specific quantum theory of gravity. The authors observe, following earlier work of Bardeen and Horowitz [10], that extreme rotating black holes have a near-horizon “throat” of a certain universal form that controls the dynamical properties of low-energy objects orbiting the black hole horizon. Then, by examining the properties of this geometry far from the horizon, they argue that any quantum theory of gravity in this space must have the two-dimensional conformal group as its symmetry. Two-dimensional conformal invariance is an infinite dimensional symmetry group, and, as such, is very powerful and constraining. Assuming that it is realized in a unitary way, Guica et al. use the symmetry to obtain a key result: they immediately count the microstates of the extreme Kerr black hole, explaining its entropy. Further, it has been shown that quantum amplitudes for scattering of particles off the near-extreme Kerr black hole are also organized by the two-dimensional conformal group [11,12]. Specifically, classic results for these amplitudes in the relativity literature are precisely reproduced by simply assuming that they are given by correlation functions in a two-dimensional conformal field theory.

These results constitute evidence, bolstered by older work [13] that a two-dimensional conformal theory controls the dynamics of low-energy excitations orbiting in the vicinity of extreme Kerr black holes. Together, these works also suggest that the scattering amplitudes from a general charged, rotating black hole, not necessarily close to the extremal bound, could take the form of correlation functions in a two-dimensional field theory. Is this a hint that the entropy and low-energy dynamics of all black holes are secretly encoded in some two-dimensional theory? Suggestions along these lines were made by Susskind [14] on the basis of thought experiments involving strings propagating in the presence of black holes. The same suggestion was made from a completely different perspective by Carlip, thinking about black hole horizons as an unusual kind of boundary in a spacetime [15]. Given the universality of the formula for black hole entropy given above, it would certainly be compelling to have a universal explanation for its form. Thus the work of Guica et al. [9] raises a key question—are all black holes really two dimensional? Or, more precisely, are the entropy and thermodynamics of all black holes, including those that are astrophysically accessible, described by a two-dimensional effective theory that gives us a window into the quantum theory of gravity?

References

R. P. Kerr, Phys. Rev. Lett. 11, 237 (1963)
J. D. Bekenstein, Phys. Rev. D 7, 2333 (1973)
J. M. Bardeen, B. Carter, and S. W. Hawking, Commun. Math. Phys. 31, 161 (1973)
V. Balasubramanian, D. Marolf, and M. Rozali, Gen. Rel. Grav. 38, 1529 (2006); Int. J. Mod. Phys. D 15, 2285 (2006); arXiv:hep-th/0604045
S. W. Hawking, Commun. Math. Phys. 43, 199 (1975); 46, 206(E) (1976)
A. Strominger and C. Vafa, Phys. Lett. B 379, 99 (1996); arXiv:hep-th/9601029
J. M. Maldacena, Adv. Theor. Math. Phys. 2, 231 (1998); Int. J. Theor. Phys. 38, 1113 (1999); arXiv:hep-th/9711200
V. Balasubramanian and P. Kraus, Phys. Rev. Lett. 83, 3605 (1999); arXiv:hep-th/9903190; J. de Boer, E. P. Verlinde, and H. L. Verlinde, JHEP 0008, 003 (2000); arXiv:hep-th/9912012; K. Skenderis, Class. Quant. Grav. 19, 5849 (2002); arXiv:hep-th/0209067
M. Guica, T. Hartman, W. Song, and A. Strominger, Phys. Rev. D 80, 124008 (2009)
J. M. Bardeen and G. T. Horowitz, Phys. Rev. D 60, 104030 (1999); arXiv:hep-th/9905099
T. Hartman, W. Song, and A. Strominger, arXiv:0908.3909 (hep-th)
M. Cvetič and F. Larsen, JHEP 0909, 088 (2009); arXiv:0908.1136 (hep-th)
J. M. Maldacena and A. Strominger, Phys. Rev. D 56, 4975 (1997); arXiv:hep-th/9702015; M. Cvetič and F. Larsen, Phys. Rev. Lett. 82, 484 (1999); arXiv:hep-th/9805146; G. T. Horowitz and M. M. Roberts, Phys. Rev. Lett. 99, 221601 (2007); arXiv:0708.1346 (hep-th)
L. Susskind, arXiv:hep-th/9309145
S. Carlip, Phys. Rev. Lett. 82, 2828 (1999); arXiv:hep-th/9812013

About the Author

Vijay Balasubramanian is the Cathy and Marc Lasry Professor of Physics at the University of Pennsylvania. He studied physics and computer science at the Massachusetts Institute of Technology and at Princeton University. His research extends across theoretical physics from string theory to biophysics and involves questions concerning information, computation, and complexity, and the role that they play in systems ranging from black holes to brain circuits.