Turbulent convection
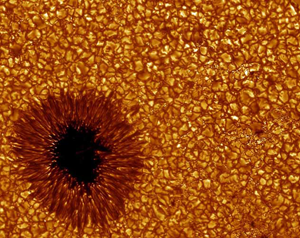
Turbulent convection in a fluid heated from below and cooled from above, called Rayleigh-Bénard convection [1,2], plays a major role in numerous natural and industrial processes. Beyond a particular temperature difference, the heated fluid rises and the cooled fluid falls, thereby forming one or more convection cells. Increasing the difference causes the well-defined cells to become turbulent. Turbulent convection occurs in earth’s outer core [3,4], atmosphere [5,6], and oceans [7,8], and is found in the outer layer of the sun [9] and in giant planets [10]. A beautiful example is seen in the photosphere of the sun (see Fig. 1), where a dominant feature is an irregular and continuously changing polygonal pattern of bright areas surrounded by darker boundaries. These granules are convection cells with a width of typically and a lifetime of only about 10 to 20 minutes.
The processes mentioned in the previous paragraph are exceptionally complex. It is true that buoyancy due to the density variation associated with the temperature variation and in the presence of gravity is the central driving force that produces the fluid flow. However, in astrophysics this flow often is modified by the influence of a Coriolis force, for instance due to the rotation of a star or planet. Further complications arise from the fact that the fluids involved sometimes are plasmas or liquid metals. In those cases the flow can interact with or even generate magnetic fields. The equations of fluid mechanics, i.e., the Navier-Stokes equations, then have to be supplemented by and are coupled to Maxwell’s equations. Additional problems may be added by the shape of the convecting system, which can introduce complicated boundary conditions.
What then is a physicist to do in these situations of apparently hopeless complexity? The astrophysicist or engineer, for instance, will have to come to grips with the entire problem by making whatever approximations may be necessary to render it tractable, while not losing any of the main physical aspects. The physicist, on the other hand, has the luxury of extracting a particular manageable aspect from the whole and idealizing it in a carefully constructed laboratory apparatus or computer program where boundary conditions and other external conditions are precisely defined. In this idealized system quantitative studies of particular fundamental aspects of the complex system then become feasible.
The idealization I want to consider is a sample of fluid in a cylindrical container with a circular cross section, a vertical axis, and an aspect ratio (where is the diameter and the height) that is heated uniformly over its bottom surface while it is cooled uniformly from above. In addition to its relevance (or some may say irrelevance because it is a major approximation) to astrophysics and geophysics (as well as numerous industrial applications), this system turns out to be of remarkable interest for its own sake. From the fluid mechanics viewpoint, it is fascinating because it is dominated over wide parameter ranges by the physics of boundary layers. Equally interesting is that it provides a tractable example of interactions between large and small scales, which are broadly important in fluid-flow problems. More generally from the viewpoint of statistical mechanics, it offers the opportunity to study the statistical properties of a driven (i.e., nonequilibrium) system in which the small turbulent scales are the noise source that drives the large-scale flow structures.
Below the onset of turbulence
To easily compare different systems, we express the strength of the thermal driving as a quantity called the Rayleigh number
which is a dimensionless form of the temperature difference. Here is the isobaric thermal expansion coefficient, the local acceleration of gravity, the applied temperature difference, the thermal diffusivity, and the kinematic viscosity ( is the shear viscosity and the density). For sufficiently small , the motionless (pure conduction) state of the fluid is stable, and convection will set in only when is greater than some critical value . For a sample of infinite width and finite height, i.e., for , it has long been known that , but for a cylinder of finite , is larger and depends on the conductivity of the side walls [13].
In what follows, I will consider the case . Historically this is the case that was studied most extensively because it allows the use of a fairly large height [ and thus large , see Eq. (1) ] without becoming too wide to fit conveniently into a laboratory. For nonconducting walls, one then has . Above onset, the azimuthal symmetry of the fluid flow can be described well by the eigenfunctions of the Laplace operator in cylindrical coordinates, i.e., it has the form . For our case, and close to , the flow consists of a single convection roll with upflow along the wall at an azimuthal orientation and downflow at the opposite side , corresponding to . As increases, the pattern becomes more complex, corresponding to larger values of and possibly also to more complicated vertical structures. When is sufficiently large, the flow goes from steady to time-varying. Precisely what happens then will depend on another dimensionless quantity, the Prandtl number (which tells us about the relative importance of viscous and thermal dissipation). Typically, the time dependence at first is periodic or chaotic—remnants of the cellular flow structure with are still recognizable, and the fluid flow remains laminar—but as is increased further beyond some , all internal structure disappears except for a single roll ( ). In that range, vigorous small-scale fluctuations become important and we regard the sample as being turbulent. The precise sequence of events leading to turbulence and the value of depend both on and on (see Ref. [14]). For and , for instance, we found that . The transition from laminar to turbulent flow was not sharp, with the turbulence evolving gradually from chaos as was increased near .
The turbulent range
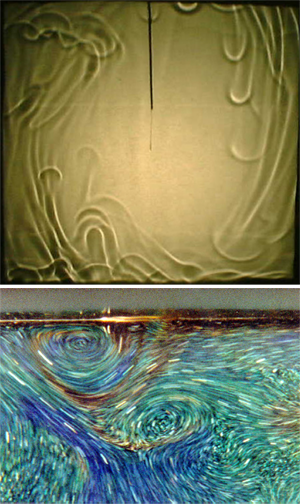
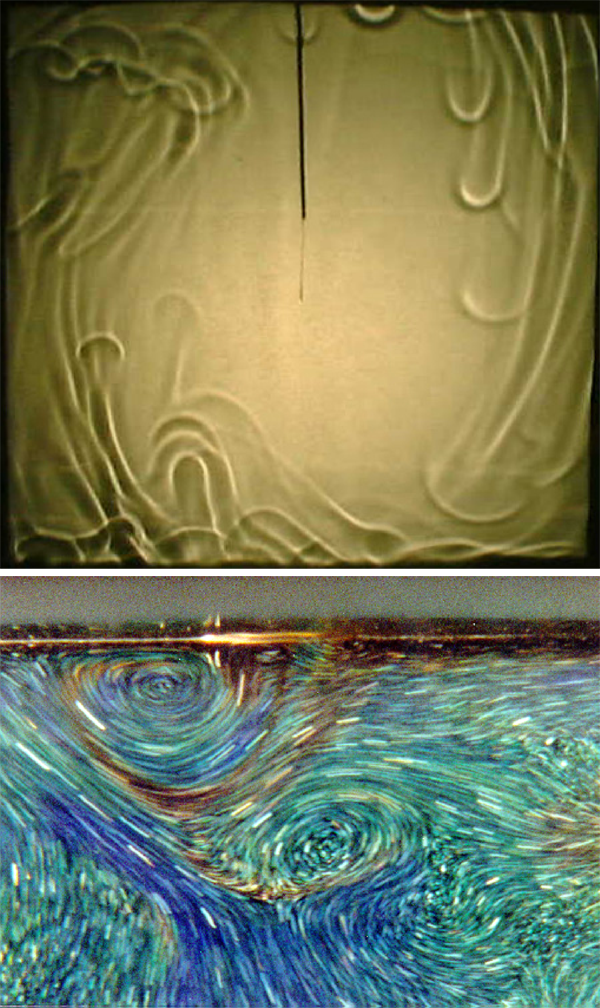
In the turbulent regime much experimental and numerical work has been done for (for details see Ref. [1]). We find that this system indeed contains a single convection roll, known as a “large-scale circulation,” just as it did close to , albeit in the presence of vigorous fluctuations on smaller length scales. The upper part of Fig. 2 is a shadowgraph visualization, looking sideways through the sample. This method is based on the bending of light rays by refractive-index gradients and thus provides an image closely related to the temperature field. One sees plumes of relatively warm fluid rising on the left and plumes of relatively cold fluid falling on the right. These plumes originate at thermal boundary layers [15] of thickness just below the top and just above the bottom plate.
An example of plume emission is shown in the bottom of Fig. 2. As a very crude approximation, the boundary layers can be viewed as quiescent fluid, with each layer supporting a temperature difference roughly equal to . This then would leave the entire sample interior at a nearly constant temperature. In reality the situation is a great deal more complicated because the temperature and velocity fields are fluctuating vigorously, both in the interior and in much of the boundary layers. Again roughly speaking, the boundary layers will adjust their thicknesses so that, according to Eq. (1), the Rayleigh number based on the boundary layer thickness (rather than ) approximately reaches its critical value. The plume emission can then be viewed as a manifestation of the near-marginal stability of the boundary layers.
Recent experimental work for revealed that the large-scale circulation carrying the plumes, and in turn being driven by their buoyancy, displays very interesting dynamics. In samples of circular cross section, the orientation of the near-vertical circulation plane undergoes azimuthal diffusion, as revealed by the observation that its mean-square azimuthal displacement is proportional to the elapsed time [16–19]. A further fascinating feature of the large-scale circulation is a torsional oscillation, with azimuthal displacements that are out-of-phase by in the top and bottom parts of the sample [20,21]. An important question was whether this mode is a characteristic of the underlying deterministic dynamics. Such a deterministic oscillator mode would have a probability distribution ) of the azimuthal displacement away from the mean value with two maxima, one each near the two displacement extrema. However, it turned out that ) was Gaussian distributed [21] with a maximum at . Such a distribution is indicative of a stochastically driven damped harmonic oscillator [22]. Thus both the azimuthal diffusion and the nature of the torsional mode suggest to us that we are dealing with a large-scale circulation of the system that is driven by the noise consisting of the small-scale turbulent background fluctuations.
Another experimentally observed property of the large-scale circulation is that it occasionally slows down and virtually comes to a halt, only to start up again, albeit usually at a different orientation [18,23]. These “cessations” are events reminiscent of the cessations observed in the geo-dynamo that are associated with reversals of earth’s magnetic field [3,4]. Much earlier it had been realized already that there are also rare occasions when the large-scale circulation orientation undergoes rotations at exceptionally high rates without completely loosing its circulation [24]. Both the “rotations” and the cessations occupy only a small fraction of the total time, and are superimposed upon the otherwise diffusive azimuthal dynamics. Yet another unexpected experimental observation was that the probability distribution of had a broad peak rather than being uniform as would be expected based on the rotational invariance of the sample.
Stimulated by some of these experimental findings and hopeful for an explanation of others, Eric Brown and I derived a simple model for the large-scale circulation [25,26]. The idea was to identify the smallest number of necessary components of the large-scale circulation, to retain the terms of the Navier-Stokes equations that are physically relevant to these components, to perform a volume average so as to reduce the field equations to ordinary differential equations, and to add phenomenological stochastic driving terms (with intensities derived from the measured diffusivities) to represent the action of the small-scale fluctuations on the large-scale excitation.
There turn out to be at least two necessary components, namely, the circulation strength and the azimuthal orientation of the circulation plane. The strength is driven by the buoyancy term and damped by viscous velocity boundary layers near the walls. The equation for is coupled to that for by a term that arises from the nonlinear term in the Navier-Stokes equation; this term represents the angular momentum of the large-scale circulation and is proportional to . We assumed further that is proportional to the amplitude of the measurable sinusoidal temperature variation around the circumference at the horizontal midplane of the cylinder. This procedure yielded two stochastic ordinary differential equations, one for the first time derivative of , the other for the second derivative of [1,25,26].
We find that there is an unstable fixed point at and a stable one at the mean value of . Normally will undergo diffusion in the depth of the potential well surrounding , but on rare occasions will be driven by the noise to the unstable fixed point. Such an event corresponds to a cessation. The equation for the second derivative of is equally interesting: reflecting the rotational invariance of the system, it has no potential extrema. It will yield diffusion, but at a typical rate controlled by an effective damping term, proportional to , that represents the angular momentum of the large-scale circulation. Thus rapid and large changes of can, but do not have to occur when (and thus the angular momentum) is small. This feature explains the observed occasional rapid rotations.
Recently this model was extended by including terms that break the azimuthal invariance of the system [27]. An example of such a term is a noncircular cross section of the cylinder. The model then predicts that the circulation plane will tend to align along the largest diameter, with fluctuations about this alignment. Another example is a system with a tilt of the vertical axis relative to gravity. Both of these cases will, for appropriate parameter values, lead to oscillations of corresponding to a damped stochastically driven harmonic oscillator. For the tilted case, these oscillations have actually been observed and their properties have been measured [27]. Note that they are unrelated to the torsional oscillations mentioned earlier.
A particularly interesting symmetry-breaking term is the Coriolis force due to the rotation of the earth, which couples to the circulation [17]. In the northern hemisphere it turns out that up- or downflow more or less parallel to the cylinder axis yields a preferred westerly orientation of , whereas flow more or less horizontal, and thus parallel to the cylinder diameter, applies a torque that tends to rotate the circulation plane in the clockwise direction when seen from above. These two competing effects yield a periodically varying potential (with period ) with a sloping background. Such a potential is sometimes known as a “washboard potential” and arises in many condensed-matter physics problems, including charge-density waves in semiconductors and constant-current-biased Josephson junctions. Knowing the azimuthal diffusivity and the potential of the system, one can calculate the probability distribution ) using a Fokker-Planck equation. The result, obtained without any adjustable parameters, agrees extremely well with the measured broad peak in ) that had been so surprising in view of the perceived rotational invariance of the system. Here we have a wonderful application of the methods of statistical mechanics to a fluid-mechanical problem.
Extensive measurements were made also for cylinders with and (see Refs. [16,28,29]). Among other interesting results, this work showed that cessations are more frequent by an order of magnitude than they are for . It remains to be seen whether this difference can be explained in terms of the model equations discussed earlier, with appropriate parameter choices.
What are the unresolved issues?
Several variations of the basic Rayleigh-Bénard convection problem are of current interest. One of them is the influence of deliberately imposed rotation about an axis parallel to the cylinder axis and at angular speeds much larger than that of earth’s rotation. For not too large values of , the Coriolis force will twist the plumes emitted from the boundary layers into vertically aligned tubes known as Ekman vortices. This is illustrated by the direct numerical simulation results shown in Fig. 3. These vortices, by virtue of the reduced pressure along their axes, will extract extra fluid from the boundary layers and significantly increase the heat transport. Enhancements in the ratio of convective to conductive heat transport (the Nusselt number, ) of over have been observed [30]. However, at larger the Nusselt number is suppressed because globally the rotation suppresses flow parallel to the rotation axis. Understanding these phenomena has significant industrial consequences, for instance, in the growth of crystals from the melt. It is relevant as well to the elucidation of convection in astrophysical objects where rotation can have a much larger influence than it does on earth. Much more is to be learned about the physics that is involved.
Another interesting problem arises when the applied temperature difference straddles a first-order phase transition [31]. The heat transport can then be enhanced by an order of magnitude or more. This problem is important, for instance, in understanding the formation of rain in clouds and for the understanding of convection in earth’s mantle. And of course it has numerous industrial applications ranging from miniaturized heat exchangers for cooling of computer components to large-scale power plants.
Other issues that are beginning to be investigated are the turbulent state in liquid crystals, where the rodlike molecules can be given a preferred orientation by the application of a magnetic field and where the fluid properties are then anisotropic. In this system the instabilities of the boundary layers are expected to differ from those of the isotropic fluid, and it will be interesting to see how this affects the turbulent state. Other variations of current interest include the influence of suspended particles and the effect of polymers on the heat transport and flow structure.
Returning to pure Rayleigh-Bénard convection without the above variations or complications, there also remain major open issues. Let us consider just two of them. First, it is obvious that convection in a cylinder with does not correspond very closely to many of the problems of interest, for instance, to the granules seen in the photosphere of the sun (see Fig. 1). We would love to know whether an irregular polygonal pattern of vigorously fluctuating convection cells such as seen in Fig. 1 would also be the pattern of large-scale circulation in a system of very large . To answer this simple question is difficult. In experiments there generally is a limit to the lateral extent of an apparatus. Thus large is often achieved only at the expense of the height . However, according to Eq. (1), small will lead to small , and yet large is desired as well. Nonetheless, no doubt this will be one of the directions of future research. If an irregular polygonal pattern does indeed exist, then an interesting question will be how this pattern is influenced by a prevailing lateral current imposed upon the system. This issue is relevant, for instance, to the formation of cloud streets (lines of cumulus clouds) in the atmosphere. It has been studied at some length near the onset of convection [32], but, to my knowledge, not for the turbulent system. The common view is that the irregular convection cells will be organized into more or less ordered rolls by the prevailing wind.
A second question of great importance is how Rayleigh-Bénard convection, even in a cylinder with of order unity, will behave at very large . With a few exceptions to be mentioned below, laboratory experiments have been limited to , and direct numerical simulations have not yet been able to reach such high values. Reliable calculations, taking many days of CPU time on modern computers, have reached only for a cylindrical sample with [33]. In the explored range, measurement and numerical simulations indicate that is proportional to , with changing gradually from about to about as changes from to [34–37]. This behavior is explained very well by a model of Grossmann and Lohse [38,39], which is based on a decomposition of the kinetic and thermal dissipations into boundary and bulk contributions. As increases, bulk contributions generally become more important and for that reason the effective exponent changes.
One might be quite satisfied with the understanding of Rayleigh-Bénard convection developed on the basis of the existing measurements for , except for the fact that theoretically the physics of this system is expected to change dramatically as grows further. With increasing the large-scale circulation is expected to become more vigorous. Its maximum speed is near the boundary layer at the top and bottom, but directly at the plates the velocity has to vanish for a viscous fluid. Thus the large-scale circulation applies a shear to the boundary layers. When the shear becomes large enough, the heretofore laminar (albeit fluctuating) boundary layers will themselves become turbulent and in a sense be swept away. An estimate [40] suggests that this will occur for when , and that is proportional to . The nature of for was investigated theoretically long ago by Kraichnan [41], and his predictions have stimulated the community ever since to search for ways to explore this high- regime. His prediction for a system without boundary layers is that , i.e., that should increase much more rapidly with than it does below . Of course our actual laboratory system does have top and bottom boundaries, and even though the laminar boundary layers may be gone, there remains the restriction that the velocity must vanish at the solid-liquid interface. This condition leads to so-called “viscous sublayers,” which are thinner than the laminar boundary layers; in Kraichnan’s theory they lead to logarithmic corrections to the relation between and , yielding [ ] .
There are at least two reasons why the Kraichnan transition is so important. First, it is associated with a fundamental change in the heat transport mechanism. Below the heat transport was limited primarily by laminar boundary layers. Above the limiting factor presumably is a thermal gradient in the bulk fluid. We certainly would like to understand this basic change in the physics of the system. Second, we know that what we learned below cannot be extrapolated to because of this change in the mechanism. It turns out that many of the astrophysical applications involve , i.e., values above by several orders of magnitude. So we really cannot extrapolate existing measurements to the ranges of these natural phenomena.
Achieving large Rayleigh numbers and strong turbulent convection
How then can we reach very large values of ? From Eq. (1) one sees that either a fluid can be chosen for which the combination is particularly large, or an apparatus with very large can be built. The former choice was pursued by Castaing and co-workers in Chicago, US, followed by Chavanne et al. in Grenoble, France, who used fluid helium at about near its critical point and reached [42]. Another group, Niemela et al. in Oregon, US, went further by using low-temperature helium as well, and at the same time also constructing a large apparatus with and [43]. Unfortunately the two sets of measurements do not agree. The Grenoble results found a transition in at from a low- regime with to a high- regime with , which they interpreted as the Kraichnan transition even though it occurred at an unexpectedly low value of . The Oregon group reached unprecedented values of as large as corresponding to ; their data were consistent with over their entire range and did not reveal any transition.
Researchers needed to address this discrepancy with a different type of experiment that was not dependent on cryogenic techniques and instead used classical fluids at ambient temperatures. To that end, Denis Funfschilling, Eberhard Bodenschatz, and I used a very large pressure vessel at the Max Planck Institute for Dynamics and Self-Organization in Göttingen, Germany. It is a cylinder of diameter and length , with its axis horizontal, and with a turret above it that extends the height to over a diameter of . Because of its shape, this vessel has become known as the “U-boat of Göttingen .” It can be filled with various gases at pressures up to 19 bars. In the section containing the turret we placed a Rayleigh-Bénard sample cell with and (the “High Pressure Convection Facility” or HPCF), yielding . Figure 4 shows the insertion of the HPCF into the turret of the U-boat. After insertion, a dome is bolted to the top of the turret section to complete the pressure enclosure.
Using sulfur hexafluoride at 19 bars, we reached [44]. Up to our results were consistent with the Oregon experiment, but differed from the Grenoble measurements: we did not find the Kraichnan transition in . At we observed a sharp transition in to a new state, but the dependence of Nu(Ra) for this state was not as predicted by Kraichnan; we found an effective exponent that was less than rather than the predicted or so. Work with the HPCF is still under way, and we look forward to what the future will bring. We expect to learn quite a bit more about how the large-scale circulation evolves as becomes large. However, at this point it is not clear whether the ultimate, or asymptotic, regime predicted by Kraichnan can ever be reached in a system with rigid top and bottom plates. But then the granules in the sun’s photosphere for instance do not have any such confining plates.
References
- G. Ahlers, S. Grossmann, and D. Lohse, Rev. Mod. Phys. 81, 503 (2009)
- D. Lohse and K.-Q. Xia, Annu. Rev. Fluid Mech. (to be published)
- P. Cardin and P. Olson, Phys. Earth Planet. In. 82, 235 (1994)
- G. Glatzmaier, R. Coe, L. Hongre, and P. Roberts, Nature 401, 885 (1999)
- E. van Doorn, B. Dhruva, K. R. Sreenivasan, and V. Cassella, Phys. Fluids 12, 1529 (2000)
- D. L. Hartmann, L. A. Moy, and Q. Fu, J. Climate14, 4495 (2001)
- J. Marshall and F. Schott, Rev. Geophys. 37, 1 (1999)
- S. Rahmstorf, Climatic Change 46, 247 (2000)
- F. Cattaneo, T. Emonet, and N. Weiss, Astrophys. J. 588, 1183 (2003)
- F. H. Busse, Chaos 4, 123 (1994)
- X. D. Shang, X. L. Qiu, P. Tong, and K.-Q. Xia, Phys. Rev. Lett. 90, 074501 (2003)
- Y. B. Du and P. Tong, J. Fluid Mech. 407, 57 (2000)
- J. C. Buell and I. Catton, J. Heat Transfer 105, 255 (1983)
- R. Krishnamurti, J. Fluid Mech. 42, 309 (1970)
- S. L. Lui and K.-Q. Xia, Phys. Rev. E 57, 5494 (1998)
- C. Sun, H. D. Xi, and K. Q. Xia, Phys. Rev. Lett. 95, 074502 (2005)
- E. Brown and G. Ahlers, Phys. Fluids 18, 125108 (2006)
- E. Brown and G. Ahlers, J. Fluid Mech. 568, 351 (2006)
- H. D. Xi, Q. Zhou, and K. Q. Xia, Phys. Rev. E 73, 056312 (2006)
- D. Funfschilling and G. Ahlers, Phys. Rev. Lett. 92, 194502 (2004)
- D. Funfschilling, E. Brown, and G. Ahlers, J. Fluid Mech 607, 119 (2008)
- M. Gitterman, The Noisy Oscillator: The First Hundred Years From Einstein Until Now (World Scientific, Singapore, 2005)[Amazon][WorldCat]
- E. Brown, A. Nikolaenko, and G. Ahlers, Phys. Rev. Lett. 95, 084503 (2005)
- S. Cioni, S. Ciliberto, and J. Sommeria, J. Fluid Mech. 335, 111 (1997)
- E. Brown and G. Ahlers, Phys. Rev. Lett. 98, 134501 (2007)
- E. Brown and G. Ahlers, Phys. Fluids 20, 075101 (2008)
- E. Brown and G. Ahlers, Phys. Fluids 20, 105105 (2008)
- H.-D. Xi and K.-Q. Xia, Phys. Rev. E 78, 036326 (2008)
- H.-D. Xi and K.-Q. Xia, Phys. Fluids 20, 055104 (2008)
- J.-Q. Zhong, R. Stevens, H. Clercx, R. Verzicco, D. Lohse, and G. Ahlers, Phys. Rev. Lett. 102, 044502 (2009)
- J.-Q. Zhong, D. Funfschilling, and G. Ahlers, Phys. Rev. Lett. 102, 124501 (2009)
- R. E. Kelly, Adv. Appl. Mech. 31, 35 (1994)
- R. J. A. M. Stevens, R. Verzicco, and D. Lohse (to be published)
- X. Xu, K. M. S. Bajaj, and G. Ahlers, Phys. Rev. Lett. 84, 4357 (2000)
- D. Funfschiling, E. Brown, A. Nikolaenko, and G. Ahlers, J. Fluid Mech. 536, 145 (2005)
- A. Nikolaenko, E. Brown, D. Funfschilling, and G. Ahlers, J. Fluid Mech. 523, 251 (2005)
- C. Sun, L.-Y. Ren, H. Song, and K.-Q. Xia, J. Fluid Mech. 542, 165 (2005)
- S. Grossmann and D. Lohse, J. Fluid. Mech. 407, 27 (2000)
- S. Grossmann and D. Lohse, Phys. Rev. Lett. 86, 3316 (2001)
- S. Grossmann and D. Lohse, Phys. Rev. E 66, 016305 (2002)
- R. H. Kraichnan, Phys. Fluids 5, 1374 (1962)
- B. Castaing, G, Gunaratne, F. Heslot, L. Kadanoff, A. Libchaber, S. Thomae, X.-Z. Wu, S. Zaleski, and G. Zanetti, J. Fluid Mech. 204, 1 (1989); X. Chavanne, F. Chilla, B. Castaing, B. Hebral, B. Chabaud, and J. Chaussy, Phys. Rev. Lett. 79, 3648 (1997)
- J. J. Niemela, L. Skrebek, K. R. Sreenivasan, and R. Donnelly, Nature 404, 837 (2000)
- D. Funfschilling, E. Bodenschatz, and G. Ahlers, Phys. Rev. Lett. 103, 014503 (2009)