Making a supersonic jet in your kitchen
When scientists speak of a “jet” they are usually referring to a fast flowing column of material, typically air or water. These jets range from the mundane, like water rushing out of a hose, to the exotic, such as the relativistic plasma jets that beam out from quasars or monster black holes. A turbo-jet, for example, pushes an aircraft forward using the supersonic thrust of air that streams out of the back of the engine.
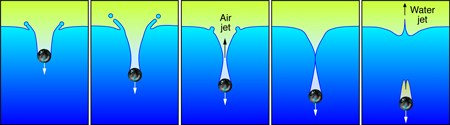
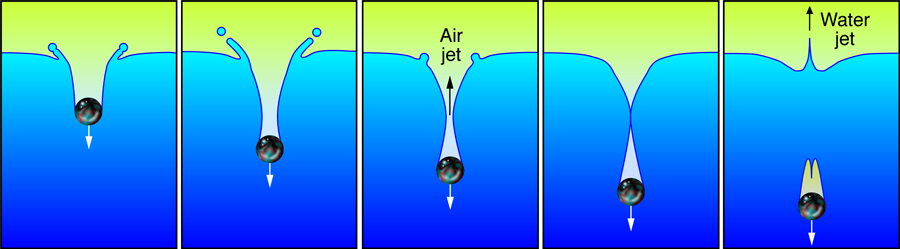
Writing in Physical Review Letters, Stephan Gekle and colleagues at the University of Twente, the Netherlands, in collaboration with the Universidad de Sevilla, Spain, have found a supersonic jet in a surprising place: the collapsing splash from an object falling into water [1]. Their general setup is easy to reproduce by dropping a marble into a deep bowl of water (a billiard ball into a full bucket works even better). This effort is rewarded with not one, but three jets (see Fig.1): First, one of upward streaming supersonic air, followed by an obvious upward jet of water, along with a less evident downward jet of water toward the marble. Although Gekle et al. perform a more controlled experiment—they pull a disk downward through the liquid surface at a controlled speed—the general features of what they find are the same. Moreover, the disk enables Gekle et al. to have good control of the experimental conditions.
In the kitchen version of the experiment, the marble creates a crown-shaped splash and crater as it falls into the liquid. The crater deepens to the point at which the walls start to contract. This is due to both the weight of the water outside and possibly surface tension, both of which create pressure gradients that force the collapse. Air inside this collapsing neck must escape upward or downward as the neck approaches pinch-off. It is in this escaping air that Gekle et al. found supersonic velocities—the first jet in this simple experiment (see Video 1).
The shape of the neck plays an interesting role. As the air escapes through the neck, right before the neck closes, it is accelerated to supersonic speeds as it is driven by high pressures from the collapsing cavity below to low pressures in the air above the water’s surface. Engineers have designed a similar process and shape into the convergent-divergent nozzle (or, de Laval nozzle) that is used as the exhaust port in many rocket engines. In our situation, however, the nozzle forms naturally and is quickly changing shape.
At the moment of pinch-off, very large pressures accompany the impact of the water surface on itself. In fact, the pinch-off is a type of near singularity where nearly all observables—velocities, surface curvatures, pressure gradients, etc.—become very large [2]. Consequently, just after the pinch-off, large pressures accelerate the water upward and downward to very high velocities [3,4]. This drives two spikes of liquid—called rebound jets—up above the water surface and another one downward into the cavity following the marble. These are our second and third jets produced by this experiment. In a low viscosity fluid such as water, the jets often quickly break up into a spray of droplets. Each of these fission events also involves a near singular pinch-off of a fluid neck [2]. In fact, there are cases where the upward spray goes higher than the initial height of the dropped marble [5].
In each case these jets are the consequence of the kinetic energy density locally rapidly rising. The analysis of these processes involves the interplay of inertia and in some cases surface tension. The root cause of these self-focusing events is that the surface is changing its topology. When the crater collapses, the surface cleaves from one sheet to one sheet plus a bubble. These high velocities (and high surface curvatures) all occur right around the time of pinch-off. Other examples where a change in topology is accompanied by divergent observables include the reconnection of quantized vortices in a superfluid [6], the formation of black holes in numerical studies of general relativity [7], crater collapse and jet formation in capillary waves [2], and the coalescence of droplets [8].
In many of these situations the rapid divergence has a small length scale cutoff because there is a crossover to a different balance of forces (e.g., at really small length scales, capillary action and the molecular structure of the fluid matters). In such cases, we speak of a near singularity rather than a singularity. For instance, viscosity, the speed of sound, or the speed of light might cap some near singularities. One is tempted to generalize that near-singular behavior may usually be present in any change in topology. In some of the examples above it is clear that the system, if forced, produces a local region of high curvature (corners) on the interface that is undergoing topology change. It is fascinating that such an ordinary event as dropping a stone into a pond holds such richness.
References
- S. Gekle, I. R. Peters, J. M. Gordillo, D. van der Meer, and D. Lohse, Phys. Rev. Lett. 104, 024501 (2010)
- B. W. Zeff, B. Kleber, J. Fineberg, and D. P. Lathrop, Nature 403, 401 (2000)
- J. Eggers and E. Villermaux, Rep. Prog. Phys. 71, 036601 (2008)
- S. Gekle, J. M. Gordillo, D. van der Meer, and D. Lohse, Phys. Rev. Lett. 102, 034502 (2009)
- J. E. Hogrefe, N. L. Peffley, C. L. Goodridge, W. T. She, H. G. E. Hentschel, and D. P. Lathrop, Physica D 123, 183 (1998)
- G. P. Bewley, M. S. Paoletti, K. R. Sreenivasan, and D. P. Lathrop, Proc. Nat. Acad. Sci. USA 105, 13707 (2008)
- M. W. Chopuik, Phys. Rev. Lett. 70, 9 (1993)
- J. Eggers, J. R. Lister, and H. A. Stone, Fluid Mech. 401,293 (1999)