The quest for dilute ferromagnetism in semiconductors: Guides and misguides by theory

Magnetism mandates that the electrons in a material collectively align their spins. In a ferromagnet there is an imbalance in the occupancy of spin-up and spin-down states; such a collective spin alignment leads to a macroscopic spontaneous magnetization that persists up to a Curie temperature $T_C$. Many common ferromagnets (such as iron or nickel) are metals, exhibiting a set amount of free electrons that make them conduct electrically. In semiconductors, on the other hand, the concentration and type of electronic carriers is controllable externally, for instance, by doping with select atom types or directly by injecting carriers. Most semiconductors are not magnetic. A material that exhibits both ferromagnetic and semiconductor properties offers the exciting prospect of combining nonvolatile magnetic storage and conventional semiconductor electronics in a single device. Magnetic semiconductors offer a number of interesting possibilities in the pursuit of “spintronics,”a branch of science and technology that exploits the spin dimension of the electron in addition to its charge, for novel electronic devices. These materials combine the properties of a semiconductor and a magnetic material, providing, for instance, a way to create $100\%$ spin-polarized currents, and by the same token, the promise of electrical control of magnetic effects. While in some magnetic semiconductors, for example, magnetite, all of the material’s constituent ions are intrinsically magnetic (“concentrated magnets”), the most recent focus has been on nonmagnetic semiconductor host materials that can be doped by a small amount of magnetic transition-metal ions or by defects that promote magnetism (“dilute magnets”).

The first experiments on dilute magnetic semiconductors focused on host semiconductors with narrow band gaps, such as $\text{GaAs}$ and $\text{InAs}$, which are infrared-absorbing black substances. When doped with manganese, ${\text{Mn}}^{2+}$ substitute for ${\text{Ga}}^{3+}$ ions, thus releasing “holes” (a positive charge resulting from the absence of an electron) that are said to collectively align the ${\text{Mn}}^{2+}$ spins ferromagnetically when the sample is cooled below $T_C$. Ferromagnetism in $\text{GaMnAs}$ cannot, however, be enhanced indefinitely by adding more $\text{Mn}$ ions, as some of the additional manganese will occupy interstitial sites or form some clustered phases that inhibit a global ferromagnetic order. This has limited the ferromagnetism in $\text{GaMnAs}$ and other doped III-V semiconductors to experimentally relevant, but not technologically useful, temperatures. For this reason, the possibility of doping common insulators like ${\text{CaO, ZnO, In}}_2{\text{O}}_3,\text{GaN}$, and ${\text{HfO}}_2$ instead was seized upon with great enthusiasm. These materials have the additional bonus feature of a wide band gap, promising the control of magnetism through charge carriers in an optically transparent medium. Reports on ferromagnetism above room temperature in such wide-gap materials quickly appeared—even in samples doped with elements that were not in themselves magnetic, or not doped at all! The excitement brought back fond memories of the early days of room-temperature superconductivity, when unusual phenomena were discovered in a group of unsuspected oxides and nitrides. What was special about these developments in pushing the $T_C$ boundaries in dilute magnets was the role of theory, which in many cases preceded experiments and influenced the type of systems that were studied. The nature of the delicate tango danced by theory and experiment in this field is the subject of this article.

The tools of solid-state theory of magnetic systems have played a central role in this rapidly developing field, offering not only ex post facto explanations of measured phenomena, but very often leading the field by predicting specific combinations of host insulators with impurity atoms that would lead to room-temperature ferromagnetism. In this pursuit, two proactive cultures of predictive theories have emerged. The initial basic philosophy was to use model Hamiltonians, in which certain specific magnetic interactions between ions are postulated (and others are excluded). For this technique, the “user” needs to guess at the outset the type of magnetic interactions that will dominate. This style of model-Hamiltonian theory has had a glorious past in numerous areas of condensed matter physics. The most prominent supposition for the interaction type between spin-polarized $3d$ impurity ions (such as $\text{Mn}$, $\text{Co}$, and other common dopants from the transition-metal series) in insulators assumed it was similar to the interaction of nuclear spins mediated by the conduction electrons in metals, and the model also assumes that the host crystal is largely unperturbed by the presence of the $3d$ impurity ion. This type of Ruderman-Kittel-Kasuya-Yosida (RKKY) [1] model-Hamiltonian approach [2] went all the way to predict ferromagnetism in various $3d$ impurity-doped compound semiconductors. In particular, the prediction that ferromagnetism persists to a high Curie temperature with $T_C$’s well above room temperature in various wide-gap oxides and nitrides [2]—has resulted in thousands of papers in the past decade, trying to capitalize on these exciting predictions offering high $T_C$ in common insulators.

Alongside the culture of model-Hamiltonian theories of dilute magnets, first-principles calculations have rapidly penetrated this field. The philosophy here is to describe each host and impurity system by considering its fundamental electronic structure, thereby obtaining the magnetic interaction type as the answer, not the question. Instead of prejudging the preferred type of magnetic interactions between ions, one articulates fundamental electron-ion and electron-electron interactions and lets the magnetic interactions emerge as solutions to the fundamental many-electron Hamiltonian. The availability of density-functional approximations (exchange and correlation functionals for the inter-electronic interactions), accurate pseudopotentials (simplifying the calculation greatly), and the ubiquitous computer packages encoding such developments into friendly interfaces freed the theorist from having to guess at the outset how a particular impurity would affect a particular host crystal. At the same time, this apparent freedom sometimes created the illusion that such modeling can be done on “automatic pilot,” disregarding potential pitfalls. Regrettably, such pitfalls sometimes created “false positive” results (suggesting high $T_C$’s when no magnetic ordering should occur), spurring enthusiasm and optimism about high-temperature ferromagnetism even when not warranted. Indeed, it has often been the case that materials synthesized from computational recipes have not behaved in the way that was expected.

In the following we will (i) discuss some of the issues and potential pitfalls that can come with uncritical application of theoretical methodology, (ii) analyze the physics of the artifact, and (iii) suggest specific ways out of these dilemmas. The good news is that the insights gained from such critical evaluation can now be embodied (in different ways!) into practical first-principles calculations, offering a truly predictive design option. Furthermore, such calculations clarify what types of interactions are indeed critical and offer model-Hamiltonian approaches a safer, albeit ex-post-facto, method to construct more realistic Hamiltonians.

The electronic properties of isolated transition-metal impurities in semiconductors were studied in great detail in the 1980s [3,4], when the growth methods produced ultradilute samples (defined as containing ${10}^{15}$– ${10}^{17}$ impurities/ ${\text{cm}}^3$) with virtually no impurity-impurity interaction. The high crystalline perfection of such samples enabled a clear experimental and theoretical understanding of the properties and chemical trends in the periodic table of isolated impurities, including their spin configuration, donor and acceptor transitions, and optical excitations. A number of intriguing physical phenomena were revealed due to coexisting localized $3d$ impurity states. One of these is the “self-regulating response” [5,6], recently revisited by Raebiger et al. [7], which shows that adding electrons to the $3d$ derived impurity levels does not change the integrated electron density around the $3d$ impurity atom because the orbitals of the surrounding ligand atoms rehybridize to minimize the impact of impurity charging. A second phenomenon is the “vacuum pinning rule,” whereby transition levels of the same impurity atom in different host semiconductors line up in approximately the same way, regardless of the host chosen [8,9], thus permitting the deduction of band offsets between different pure materials from the knowledge of impurity level positions [10]. Third, another consequence is called “exchange-correlation negative $U$,” [11] whereby the strongly varying exchange splitting of differently charged impurities can lead to effective electron-electron attraction. These systems all show interesting physics, however, such systems revealed no ferromagnetism, as the generally low solubility of dopants precluded collective interactions.

Collective magnetic ordering requires the individual magnetic impurity ions to be close enough to one another so as to interact. In practice, this implies large concentrations, often well above typical thermodynamic solubility limits. The low solubility limit of most $3d$ ions in semiconductors can, however, be overcome by using nonequilibrium growth techniques (such as very low-temperature molecular beam epitaxy). These techniques increased the impurity concentration by a few orders of magnitude to ${10}^{20}$ dopants/ ${\text{cm}}^3$. This, however, comes at the price of severely lowering the structural quality of the samples. Such high concentrations of magnetic ions in semiconductors, such as $\text{GaAs:Mn}$ [12,13], leads to ferromagnetism with relatively high Curie temperatures of around $100\text{K}$—a temperature range that has opened the era of spintronics [14,15].

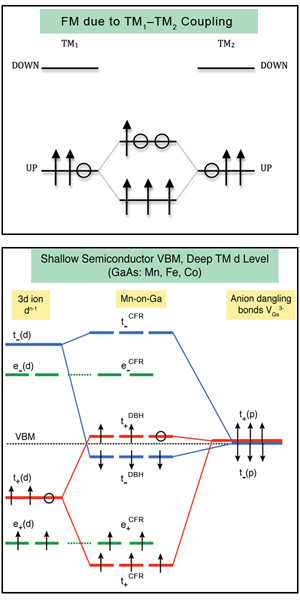
The basic driving force of this form of ferromagnetism of $3d$ impurities in III-V semiconductors is now understood [16] as the energy stabilization ensuing from the interaction between partially occupied hybrid orbitals located on different impurity sites, ${\text{TM}}_1$ and ${\text{TM}}_2$, in the host crystal. Figure 1 (top) illustrates that if two such orbitals interact, there will be a gain in energy, i.e., a stabilization of the FM state (relative to the antiferromagnetic state [16]).

Illustration: Carin Cain

Illustration: Carin Cain

×

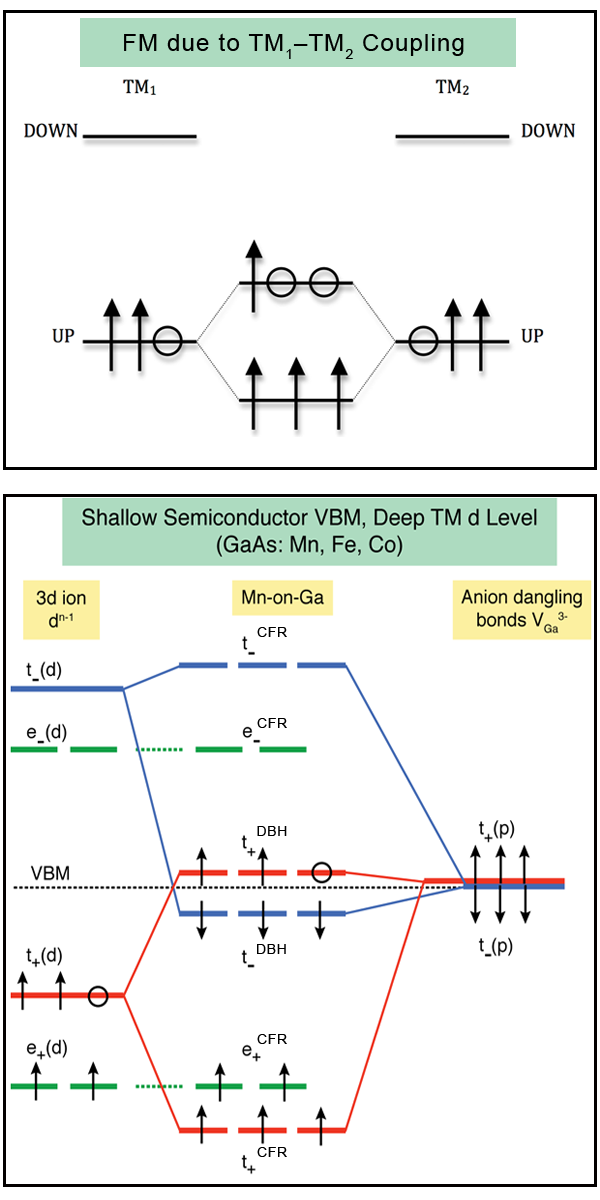
One might ask, how would such individual partially occupied hybrid orbitals come to exist in the first place? The answer to this is illustrated in Fig. 1 (bottom). The formation of a substitutional $3d$ impurity can be thought of as a two step process, involving first the removal of a host $\text{Ga}$ atom, and second, the placement of a $3d$ impurity atom in its place. The combined impurity/host orbitals simply result from coupling between the host-crystal cation vacancy state (“dangling bonds” of t(p) symmetry) and the impurity orbital of the $3d$ atom filling this vacancy (having t(d) symmetry as well as nonbonding e(d) symmetry). The interaction between these states leads to a bonding state, and an antibonding state. The partial occupancy which ultimately drives ferromagnetism resides in the higher of these states. For $\text{Mn}$ in $\text{GaAs}$ the antibonding state, dominated by t(p), is called a “dangling bond hybrid” (DBH) state, and the bonding/nonbonding states, dominated by t(d) and e(d), are called “crystal field resonances” (CFR). As we move to the left from $\text{Mn}$ in the periodic table, keeping the $\text{GaAs}$ host, we approach the light $3d$ impurity elements such as $\text{V}$. For these, the atomic t(d) and e(d) are higher in energy and the roles of DBH and CFR are interchanged. The same interchange occurs in the case where $\text{Mn}$ is placed in a host crystal with light anion elements, such as nitrogen in $\text{GaN}$, where the t(p) level is deeper and t(d) dominates the hole. It is the interaction between the partially occupied hybrid states, centered on different impurity sites in the crystal, which energetically stabilizes the ferromagnetic configuration.

This simple mechanism implies simple rules [17] for impurity-host material combinations that might produce ferromagnetism: one obtains the electronic configuration by constructing an Aufbau ground state for $n$- $m$ electrons ( $n$ is the number of TM valence electrons, and $m$ is the valence of the cation site) occupying the relevant symmetry orbitals. For example, a ferromagnetism-promoting partial occupancy of DBH can be expected when $\text{Mn}$ occupies a trivalent $\text{Ga}$ site, but not the divalent $\text{Zn}$ site. This mechanism was directly verified by first-principles calculations of the energy of impurities in a solid as a function of the occupancy of the DBH, and noting the stabilization (destabilization) of the ferromagnetism for partial (full) occupancy.

First-principles electronic structure theory of $\text{Mn}$ doped into III-V nitrides, phosphides, and arsenides [18–20] have shown that the ferromagnetism-promoting hole (i.e., the orbital with partial occupancy, ${\text{t}}_{+}^{\text{DBH}}$ in Fig. 1) resides inside the host band gap. When the host anion changes from $\text{As}$ to $\text{P}$ and then to $\text{N}$, the band gap increases primarily by shifting the valence band maximum (VBM) to lower energies. Thus, as one moves from arsenides to phosphides and then to nitride semiconductors, the hole-carrying impurity level, being roughly pinned, appears farther and farther from the VBM, deeper in the band gap. This makes the hole-carrying impurity wave function progressively more localized, weakening its communication with other magnetic ions; thus we lose ferromagnetism. Thus the conclusion of such microscopic calculations [4,16,17] was that $\text{Mn}$ will have lower $T_C$ as we go from a host arsenide to a host phospide and then to a nitride. While initial estimates of $T_C$ derived from directly associating the Weiss field with first-principles calculated magnetic coupling energies predicted optimistically higher $T_C$ in the wider gap (i.e., nitride) host crystals [21], it was quickly realized (by the same authors) that a proper statistical treatment of these exchange energies (via Monte Carlo, see Ref. [22]) predicted a much reduced $T_C$ as one moves to wider gap host crystals.

In parallel with such first-principles calculations, more traditional model-Hamiltonian approaches were developed [2,23] that assume a scenario for the underlying interactions, and then solve the scenario mathematically. The classic $\mathbf{k}\cdot \mathbf{p}$ approach in semiconductor physics, as described in Ref. [24], expands the states of a system in terms of a small number of preselected bands of the host crystal at the Brillouin-zone center. In the field of dilute magnetic semiconductors, the use of such $\mathbf{k}\cdot \mathbf{p}$ concepts assumes that the hole that promotes magnetism can be described by just a few host crystal states, becoming essentially a “hostlike hole” [2,23]). Such simple concepts differ substantially from the atomistic picture of Fig. 1 (bottom). The model Hamiltonian approach is then able to produce, analytically, the dependence of the ferromagnetism Curie temperature $T_C$ on basic material parameters. This lead to the highly influential bar-diagram published by Dietl et al. [1] (cited more than $3200$ times) predicting the highest $T_C$ for binary semiconductors having the shortest bond length and thus the largest band gap. This design principle pointed towards wide-gap binary compounds containing a first-row element such as $\text{C}$, $\text{N}$, or $\text{O}$ as the best candidates for high- $T_C$ ferromagnets. This prediction started a world-wide quest for high- $T_C$ ferromagnets in wide-gap metal oxides ( ${\text{ZnO, HfO}}_2$), nitrides ( $\text{GaN}$), and carbides based on dilute transition metal impurities. As exciting as such predictions were, they did not have the additional virtue of becoming true. Indeed, the assumed scenario that the ferromagnetism-promoting hole has the personality of the host valence band did not seem to be true for wide-gap insulators doped with transition metals such as $\text{Mn}$. The simple lesson from microscopic models that the $\text{Mn}$ acceptor (hole-carrying) level becomes progressively more localized (i.e., contributing to lower $T_C$) as one moves up the group $\text{V}$ elements from arsenic to nitrogen was lost in the global enthusiasm to seek high $T_C$ in the widest gap host systems.

Magnetic ions were not the only dilute species in wide-gap insulators that were implicated with high- $T_C$ ferromagnetism. Indeed, simple structural defects such as cation vacancies [25–28] or carbon or nitrogen impurities [29–31] also became prime candidates for point sources of ferromagnetism behavior in wide-gap insulators. The basic thought here is that a proper combination of defect/impurity and a host crystal will lead to a hole-carrying (partially occupied) level, centered about this defect/impurity site, and that a ferromagnetic spin arrangement will be stabilized when different such centers interact [Fig. 1 (top)]. The search for the particular combination of defect/impurity and host crystal was, in many instances, guided by theory. Indeed, an impressive sign of the maturity of electronic structure theory based on first-principles was the central role that it had occupied in guiding the international quest for ferromagnetism in dilute wide-gap insulators [32–35].

Unfortunately, a number of overlooked factors contributed to confusion. We next discuss a number of ways in which such calculations can produce unfounded optimism, such as a too high- $T_C$ ferromagnetism. Fortunately, recognition of such factors has lead to proposing a fix. Efforts worldwide to improve these fixes promise to create a robust guide for new design principles for such materials.

Problem $1$: False occupancy

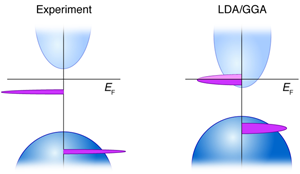
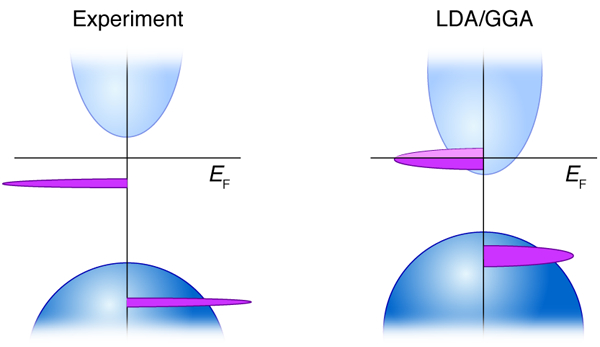
A well-known problem of the local density approximation (LDA) and its relatives like the generalized gradient approximation (GGA) is the underestimation of the band gap of nonmetals; an underestimation often manifested by a conduction band minimum that is set too low. This can become a problem in the context of magnetism if the defect/impurity center contemplated will be resonating within the (artificially too low) conduction band of the host when LDA is used, whereas in reality this level should be in the band gap (Fig. 2). It turns out that this is not a problem for $\text{Mn}$ in III-V semiconductors, where the conduction band minimum is high enough that the hole-carrying impurity orbital is inside the band gap, even in LDA [36]. However, it is often a problem in oxides, when the substantial LDA underestimation of the conduction band minimum energy can spuriously place the impurity orbital inside the host crystal conduction band (for example, $\text{Mn}$ in $\text{ZnO}$ [32,33,37]). The electrons will then drop into the conduction band minimum, creating a hostlike delocalized orbital that promises long-range interaction with other centers, to the benefit of (spurious) high- $T_C$ ferromagnetism. This type of LDA-error was demonstrated also in $\text{ZnO:Cr}$ [31]. Using GGA or GGA+ $U$ (which seeks to correct problems by adding a repulsive potential to GGA) instead of LDA does not solve the problem, as it shifts the unoccupied $3d$ impurity level to yet higher energies, nor does the “scissors operator” correction, which shifts the host conduction band minimum to higher energies after the calculation is done. Such false occupancy errors have led to a substantial number of publications predicting optimistically long-range ferromagnetism. Clearly, one needs to maintain correct host band edge positions before interaction with the defect/impurity electrons is treated, and then see if ferromagnetism will survive a correct positioning of the levels.

Illustration: Carin Cain

Illustration: Carin Cain

×

Once this principle is understood, a number of strategies can be applied to overcome the false occupancy problem. One such example is our earlier work in which we designed empirical nonlocal external potentials (NLEP) [38], in the spirit of the method of Christensen [39], where external potentials are placed on host atoms (and interstitial sites) and the potential parameters are adjusted to reproduce the correct host band structure. Applying such band-gap corrections to self-consistent impurity calculations allows one to place the impurity levels in the correct manifold of host states. For $\text{ZnO:Cr}$, the impurity electrons were now in a (Jahn-Teller split) level within the band gap, having no partial occupancy, hence no ferromagnetism [38]. Other approaches to avoid false occupancy may involve using, at the outset, band-gap corrected methods, such as hybrid functionals [40] or self-interaction corrections (SIC) [41,42] instead of LDA and its relatives.

However, all is not lost: one can turn false occupancy around. One important outcome of the understanding of the significance of the impurity versus host level alignment is the prediction of electron-induced ferromagnetism in oxides. As noted above, ferromagnetism in dilute III-V materials was universally due to holes. However, certain impurity-host combinations might have a legitimate impurity level in resonance with the host conduction band; if that level is not too high inside the conduction band, it might be partially occupied by additional intentional donor doping, creating the desired partial occupancy and hence ferromagnetism. This idea led to a search for $3d$ impurities in $\text{ZnO}$ and ${\text{In}}_2{\text{O}}_3$ [38,41,43–46] that have levels in resonance with the lowest part of the host conduction band. It is important here to note that the relevant quantity describing the energy of the TM-impurity “level” is the quasiparticle energy, that is, the electron addition energy into the unoccupied defect state. Thus the empty $t_2$ level of $\text{ZnO:Co}$ lies inside the conduction band [38,41], whereas (incorrect) estimates based on typical $d$- $d$ transition energies of tetrahedral $\text{Co}$ placed the $t_2$ state at a much lower energy inside the gap [45]. Since, however, such $d$- $d$ transitions correspond to charge-conserving excitations, they are not suited to determine quasiparticle energies [46], indeed, the $\text{Co}$ $t_2$ “level” is inside the $\text{ZnO}$ conduction band.

One of the few cases estimated to have a $3d$ level inside, but not too high within, the conduction band was $\text{Cr}$ in $\text{ZnO}$ [38] and ${\text{In}}_2{\text{O}}_3$ [43]. However, according to the calculation, ferromagnetic coupling requires a rather large number of carriers—of the order of ${10}^{21}{\text{cm}}^{-3}$. This may be difficult to attain in structurally high-quality oxides, which may explain why ferromagnetism in dilute oxides is generally associated with highly defective samples and never occurs in single crystals.

The good news is that once understood, false occupancy in LDA can be cured, so the trap of false positive ferromagnetism due to this effect can now be put behind us.

Problem 3: Failure to localize

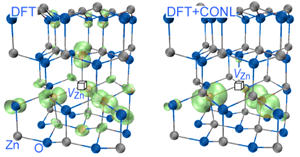
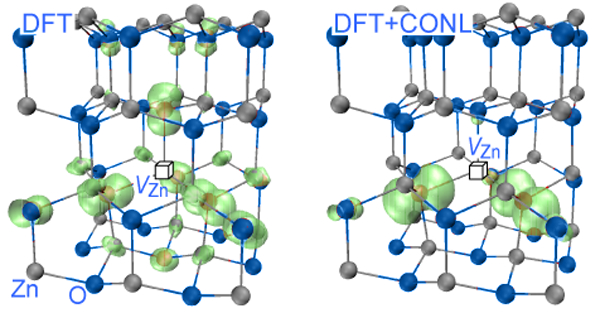
Symmetry breaking of defect orbitals is known in simple oxides. A $\text{Mg}$ vacancy in $\text{MgO}$ has six crystallographically equivalent oxygen neighbors, yet the two holes created by a charge-neutral $\text{Mg}$ vacancy are localized mostly on just two of the six oxygen atoms [56]. Significantly, LDA approaches will fail to localize the holes—thus overestimating the interaction between holes associated with different cation vacancies—and will predict spurious ferromagnetism. The failure of LDA to localize stems fundamentally from the convex, rather than linear, dependence of its total energy on occupation numbers [57–59] and is a manifestation of the need for self-interaction correction. Since failure to localize may artificially enhance intersite wave function overlap, it is important to estimate its impact on defect-defect ferromagnetism. What is required is a formalism that corrects the concave $E(N)$ tendency of Hartree-Fock (favoring localization) and the convex $E(N)$ tendencies in LDA (favoring delocalization), replacing it by a linear dependence. This requirement can be cast as a generalized Koopmans’ condition, i.e., the electron addition energy be equal to the orbital energy, $E(N+1)-E(N)=e_i(N)$ [60]. Such cancellation of nonlinearity (CONL) may be achieved approximately by mixing Hartree-Fock with LDA [61], or by self-interaction corrections to DFT [62,63], or more explicitly, by adding to DFT an on-site potential with a parameter obtained by requiring the generalized Koopmans’ condition [60], therefore enforcing the CONL by construction. Using such a CONL approach leads to self-trapped holes in both rutile and anatase ${\text{TiO}}_2$ [64], and leads to much deeper acceptor levels and more localized hole orbits for acceptors in oxides and nitrides, e.g., $\text{N:ZnO}$ [65], $\text{Cu:ZnO}$, ${\text{Mg:In}}_2{\text{O}}_3,{\text{In:SnO}}_2$ [60], and $\text{Be:GaN}$ [66]. When applied to metal vacancies implicated previously via LDA calculations in ferromagnetism [31,67], Chan et al. [68] found that the cancellation of the nonlinearity led to a much reduced $V_{\text{Zn}}-V_{\text{Zn}}$ interaction in $\text{ZnO}$, from $32\text{meV}$ obtained in LDA [31] for a pair separated by $8.4$ Å, to less than $1\text{meV}$. This reduction of magnetic interaction results from the strong localization of the $V_{\text{Zn}}$ spin-density, as shown in Fig. 3. After CONL, the $V_{\text{Zn}}$ does not even possess a robust magnetic moment any more, because the singlet state ( $S=0$) is almost degenerate with the triplet state ( $S=1$) [68]. Clearly, the hopes for ferromagnetism due to cation vacancies based on the standard DFT [28,31,47,67] evaporate when the spurious delocalization is corrected.

Illustration: Carin Cain

Illustration: Carin Cain

×

The good news is that once the role of CONL on magnetism is understood, this can be readily cured either empirically or by complete generalized Koopmans’ methods.

Guiding experiments towards promising defects or impurities that can promote carrier-induced ferromagnetism in certain wide-gap materials has proven to be difficult. Even if you correctly formulate the underlying electronic structure problem so that false-occupancy is avoided, the LDA failure to localize holes can get you. And if these are fixed, you still need to establish the defect concentration that satisfies percolation, yet is tolerated mechanically by the lattice. And you still need to consider the microstructure, i.e., the microscopic distribution of defects, since ideal single oxide crystals with ideal impurities do not lead to ferromagnetism. Indeed, if it’s not one thing that leads to false FM prediction, it’s another.

Finally, one should ask whether it is appropriate to describe the collective magnetism of a sample in terms of interacting single isolated point defects? Statistics tells us that the probability of two or more defects on one of the sublattices in a zinc blende, wurtzite, or rock salt crystal occupying neighboring sites is $>50\%$ for defect concentrations $>5\%(\sim {10}^{20}/{\text{cm}}^3$) [69]. Once a defect pair has another defect next to it (e.g., with a $50\%$ probability), it has a lowered point group symmetry and consequently a different electronic spectrum, and is likely to exhibit completely different magnetic interactions compared to its isolated relatives [48,70]. This has the detrimental effect that magnetic interactions no longer can be mapped on Dirac-van Vleck-Heisenberg type models ( $E=\mathrm{\Sigma }{J}_{ij}{\mathbf{\text{s}}}_i\cdot {\mathbf{\text{s}}}_j)$ [71]. As expected, this problem can be circumvented by introducing additional correction terms or explicit configuration dependences to the model, as was done in Refs. [49,51], which, however, mandates the explicit calculation of various additional clustered/microstructured configurations and their energetics. Moreover, the flaws in the underlying spin models seem to be of a fundamental nature, since, as it turns out, magnetic coupling energies, even of the simplest hydrogen molecules, have no mapping thereupon [72]. This failure of Heisenberg’s theory [73] can further be traced back onto the Heitler-London theory [74], of which it is a generalization, and which has been abandoned on several occasions [75–77].

Bad is Good? No, this is not an attempt at moral revisionism. But consider this: The functionality of optoelectronic semiconductor devices such as lasers, light-emitting diodes, or photovoltaic solar cells is predicated on the structural quality of the active material. “Good materials,” i.e., those leading to efficient functionality, invariably need to have good crystalinity, purity, and very few defects. Yet if one were to use such near-perfect bulk samples of oxides, no ferromagnetism of the type discussed here would be present. Considered from this viewpoint, structurally imperfect and compositionally nonstoichiometric oxide materials (which would be considered “bad materials” in the semiconductor device culture) are “good materials” in this field of dilute magnetic oxides, as they are the only ones that yield, so far, the desired functionality.

Although much of the article has pointed out the various pitfalls encountered in running LDA on automatic pilot, the conclusions are more optimistic: Electronic structure calculations are a powerful tool to describe magnetic ground states, even in complicated clustered or nanostructured configurations. The ensuing results clarify which types of interactions are indeed critical, offering model-Hamiltonian approaches a safer, albeit ex-post-facto method to construct safe, simpler Hamiltonians. Furthermore, the results may be used as input for statistical models constructed to avoid the obvious pitfalls in earlier Heisenberg-like attempts.

This work was funded by the U.S. Department of Energy, Office of Science, Basic Energy Science, Materials Science and Energy Division, under Contract No. DE-AC36-08GO28308 to NREL. HR is supported by a Grant-in-Aid for Young Scientists (A) grant (No. 21686003) from the Japan Society for the Promotion of Science.