Slicing the cuprate Fermi surface to reveal underlying order

Andrey V. Chubukov

Viewpoint

Slicing the cuprate Fermi surface to reveal underlying order

Department of Physics, University of Wisconsin, Madison, WI 53706, USA

June 28, 2010• Physics 3, 54

High-resolution angle-dependent quantum oscillations in underdoped cuprates and unrestricted fits are used to suggest a new Fermi surface topology.

Figure caption — **Figure 1:** (a) A schematic Fermi surface extracted from quantum oscillation measurements by Sebastian *et al.* The authors argue that they can extract from the data both electron and hole pockets ( $α$ and $β$ are hole pockets, and $γ$ are electron pockets). (b) Reconstructed Fermi surface for incommensurate SDW order in low-disorder ortho-II phase of ${YBCO}_{6 + δ}$ .

A complete theoretical picture of high- $T_{c}$ superconductivity in the cuprates is still lacking despite more than two decades of research. One of the central puzzles in these materials is related to the nature of the low-lying electronic excitations that seems to differ radically between the underdoped and overdoped regimes that define the edges of the superconducting dome. While there is little doubt that overdoped cuprates are bad metals with a large Fermi surface, the nature of low-lying excitations in underdoped cuprates is a matter of intensive debate. The recent discovery of quantum oscillations (QO) in the electrical resistance of the low-disorder ortho-II ${YBa}_{2} {Cu}_{3} O_{6.5}$ [1] under a magnetic field strong enough to suppress superconductivity has opened up a new direction of research in the high $T_{c}$ area and re-inserted the concept of a Fermi liquid (FL) into the underdoped region, where it was long thought that fermionic coherence is completely lost. The issue of QO has been the subject of intensive debates in the literature over the last three years (see Refs. [1–5,7–10], to name a few).

The debates will surely intensify because of new quantum oscillation experiments that show more periods than before, allowing the detection of multiple oscillation frequencies, and a new interpretation of this data presented in an article in Physical Review B by Suchitra E. Sebastian and her international team of colleagues from Cambridge and Oxford universities in the UK, Los Alamos Laboratory in the US, the University of British Columbia and the Canadian Institute for Advanced Research, both in Canada, and Max-Planck-Institut für Feskörperforschung in Stuttgart, Germany [11].

According to the standard Lifshitz-Kosevich theory [12], quantum oscillations in a FL originate from Landau quantization of closed orbits in a magnetic field. A period $F$ of QO is related to an extreme cross section of the Fermi surface (FS) by $F$ =n $Φ_{0}$ , where n is the carrier density enclosed by the FS, and $Φ_{0}$ is the magnetic flux quantum. QO measurements in the overdoped ${Tl}_{2} {Ba}_{2} {CuO}_{6 + δ}$ [6] revealed a large hole FS, consistent with photoemission [13] and with the Luttinger count for free electrons. In sharp contrast, Fermi surfaces extracted from QO measurements in underdoped YBCO are small pockets, which collectively account for only few percent of the area of the Brillouin zone (BZ). Such small pockets imply that the FS undergoes a substantial reconstruction between overdoped and underdoped regimes. FS reconstruction and small pockets are expected when the system develops a density-wave order in either spin or charge channel (spin-density wave (SDW) [14] or $d$ -density wave (DDW) [7], respectively). In both cases, however, the reconstructed FS contains both electron and hole pockets, at least when the order parameter is not too large.

The measurements of QO revealed multiple oscillation frequencies, several of them as satellites of the major peak at $F$ $\sim 530 T$ [3,5]. This peak was originally identified [5] as coming from an electron pocket on the basis of required consistency with the observed negative sign of the Hall coefficient, and satellites were attributed to bilayer splitting and warping of an electron FS.

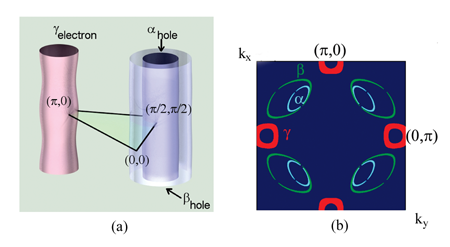
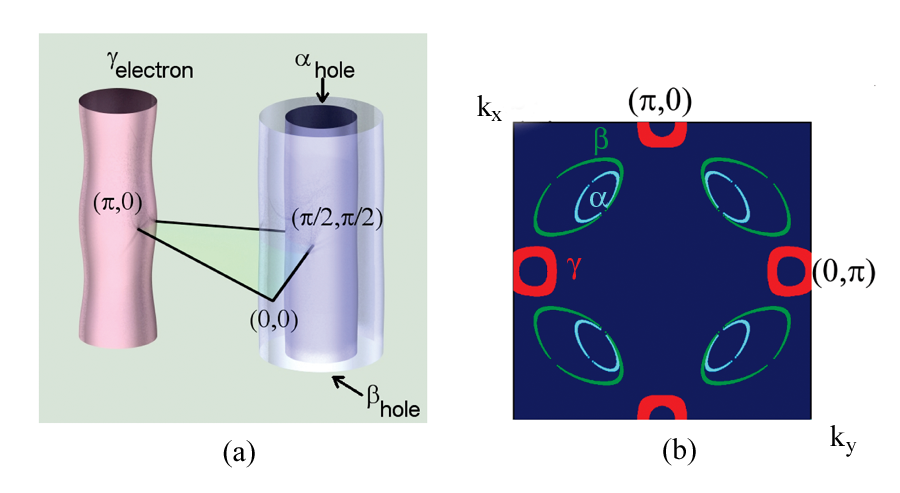
Sebastian et al. have offered another interpretation of the QO data [11]. They argue that the major peak corresponds to the hole pocket located near ( $π$ /2, $π$ /2) (the $α$ pocket in their notations), while the two satellites at $460 T$ and $602 T$ correspond to electron $γ$ pockets near (0, $π$ ) and symmetry-related points (see Fig.1). They further associate the high-frequency oscillation at $1650 T$ , which they identified earlier [3], with another, larger hole $β$ pocket, and argue that their ( $α$ , $β$ , $γ$ ) pocket structure is quantitatively consistent with the FS for an incommensurate SDW state. The agreement with the data becomes even better once one includes the ortho-II potential due to oxygen ordering [8].

The authors present several arguments to support their claim. Their key argument is that the best unconstrained fit to their data yields a near-perfect cylindrical $α$ FS, which accounts for the central peak at $F_{α}$ =532 $T$ in the Fourier transform of QO, and a corrugated $γ$ cylinder with a rounded-square cross section, whose mean frequency $F_{γ}$ is the same as for the $α$ pocket, but corrugation splits $F_{γ}$ into belly and neck frequencies ( $F_{γ, belly} = 602 T$ and $F_{γ, neck} = 460 T$ with small error bars). The authors emphasize that to exceed frequency resolution and extract all three frequencies from the Fourier transform of QO, it is crucial to be able to detect up to $12$ oscillations.

Since corrugation comes from interlayer hopping $t_{z},$ and $t_{z}$ is momentum dependent and scales as (cos $k_{x}$ - cos $k_{y}$ ) $^{2}$ [15], the near absence of corrugation places the $α$ pocket near ( $π$ /2, $π$ /2), while the strongly corrugated $γ$ pocket is most likely to be near (0, $π$ ), where $t_{z}$ is the largest. A comparison with the FS for an SDW ordered state then identifies the $α$ pocket with the hole pocket and the $γ$ pocket with the electron pocket. The same comparison identifies the additional $β$ pocket with the larger hole pocket (see Fig. 1). In such a FS geometry, the $α$ and $γ$ pockets almost compensate each other, while the $β$ pocket satisfies the Luttinger count in the SDW state.

To further support this scenario, the authors presented experimental evidence for subleading harmonics at $2 F_{α}$ , $2 F_{γ, belly}$ , and $2 F_{γ, neck}$ , and emphasized that the higher frequency oscillation at $F_{β} = 3.14 F_{α}$ is not a higher harmonic of $F_{α}$ . They reported several additional checks (e.g., angular dependence of QO frequencies), which all show that their scenario is self-consistent. They attributed the smaller intensity of the $γ$ peaks compared to the $α$ peak to the fact that for corrugated pockets, phase coherence is achieved only near extremal cross section, while for the cylindrical $α$ pocket, phase coherence exists for all $k_{z}$ .

Sebastian and her coauthors go further in their analysis to argue that near-equal size of hole and electron Fermi surfaces makes the system susceptible to an excitonic FS instability at low doping, in some similarity to FS instabilities in the iron pnictides. In an earlier study [16], they found that the quasiparticle mass along the $α$ FS rapidly increases with reducing the amount of hole doping. They now attribute this behavior to an excitonic instability.

The near-equivalence of the sizes of $α$ and $γ$ pockets (averaged over $k_{z}$ ) is possibly a weak point in the interpretation by Sebastian et al. as this is not a generic property of a SDW reconstructed FS. One can obtain near-equal $α$ and $γ$ pockets for an incommensurate SDW, but this requires fine tuning and doesn’t hold for all dopings.

There are other explanations of the QO data which exploit the fact that $F_{α} \approx F_{γ}$ . Audouard et al. reported [5] similar results for the Fourier transform of the oscillations, with satellite $γ$ bands, but they identified the major $α$ peak as the electron pocket (for consistency with the sign of the Hall coefficient [2]), and attributed the emergence of satellites to warping and bilayer splitting of the electron pocket. Several theoretical scenarios have been put forward to explain under what conditions one can only see an electron pocket: one scenario is that a hole pocket is wiped out by scattering from vortices in the mixed state [7]; another widely discussed suggestion is a stripe-type magnetic order, which yields an electron pocket and open hole bands [9]. Sebastian et al. argue against bilayer splitting as the origin for satellites on the basis that (i) for antiferromagnetically coupled bilayers the effect is weak, and (ii) the unconstrained fit gives a very different degree of corrugation for $α$ and $γ$ pockets, indicating that they likely come from different parts of the BZ. This issue, however, is not fully resolved yet and requires a very detailed analysis.

Overall, the new experiments by Sebastian et al. and the new interpretation they provide [11] strongly point to a conventional density-wave order in the nonsuperconducting state of the underdoped cuprates. Their data are not in contradiction with those of Audouard et al. [5], but the interpretation is different. Theoretical arguments for either SDW or DDW order in underdoped cuprates have been presented by a number of authors [7,8,14], and if QO do indeed detect both electron and hole Fermi surfaces, it is a true boost for density-wave scenarios. The SDW scenario is also supported by recent discovery of long-range incommensurate spin order in YBCO in the same doping range where QO have been observed [17]. At the same time, the near equivalence between the sizes of $α$ and $γ$ pockets still needs to be fully understood, and the relation to Hall measurements has to be clarified. Besides, there have been recent reports about the difficulty in explaining specific heat data within a density-wave model [18] and the vanishing of the $α$ peak at $8 %$ doping [19]. This avalanche of new results is a good indication that the field of high- $T_{c}$ superconductivity is very much alive and after almost $25$ years is still at the forefront of research in strongly correlated electrons. It is also becoming increasingly clear that the low-energy physics of the cuprates is more conventional than the community used to believe.

References

N. Doiron-Leyraud et al., Nature 447, 565 (2007)
D. LeBouef et al., Nature 450, 533 (2007)
S. E. Sebastian et al., Nature 454, 200 (2008)
L. Taillefer, J. Phys. Condens. Matter 21, 164212 (2009); Annual Review of Condensed Matter Physics, Vol. 1 (to be published)
A. Audouart et al., Phys. Rev. Lett. 103, 157003 (2009)
B. Vignolle et al., Nature 455, 952 (2008)
X. Jia, P. Goswami, and S. Chakavarty, Phys. Rev. B80, 134503 (2009) and references therein
J.-M. Carter, D. Podolsky, and H-Y Kee, Phys. Rev. B 81, 064519 (2010)
A. J. Millis and M. R. Norman, Phys. Rev. B 76, 220503 (2008); M. Vojta, Adv. Phys. 58, 699 (2009)
M. Stephen, Phys. Rev. B 45, 5481 (1992); A. Melikyan and O. Vafek, 78, 020502 (2008); K-T. Chen and P. A. Lee, 79, 180510 (2009)
S. E. Sebastian, N. Harrison, P. A. Goddard, M. M. Altarawneh, C. H. Mielke, R. Liang, D. A. Bonn, W. N. Hardy, O. K. Andersen, and G. G. Lonzarich, Phys. Rev. B 81, 214524 (2010)
See, e.g.,D. Shoenberg, Magnetic oscillations in metals (Cambridge University Press, Cambridge, 1984)[Amazon][WorldCat]
M. Plat et al., Phys. Rev. Lett. 95, 077001 (2005)
B. I. Schraiman and E. Siggia, Phys. Rev. B 46, 8305 (1992); A. V. Chubukov and D. Morr, Phys. Rep. 288, 355 (1997); Y. Qi and S. Sachdev, Phys. Rev. B 81, 115129 (2010); T. A. Sedrakyan, and A.V. Chubukov, 81, 174536 (2010)
E. Pavarini et al., Phys. Rev. Lett. 87, 047003 (2001)
S. E. Sebastian et al., Proc. Natl. Acad. Sci. U.S.A. 107, 6175 (2010)
V. Hinkov et al., Science 319, 597 (2008); Haug et al., Phys. Rev. Lett. 103, 017001 (2010); V. Hinkov (private communication)
O. Vafek (private communication)
D. LeBoeuf et al. (to be published); B. Vignolle et al. (to be published); For a theoretical explanation within the stripe model see M. R. Norman, J. Lin, and A.J. Millis, Phys. Rev. B 81, 180513 (2010)

About the Author

Andrey Chubukov received his Ph.D. in 1985 from Moscow State University and is currently Professor of Physics at the University of Wisconsin-Madison. His research interests are in theoretical condensed matter physics and include the interplay between magnetism and superconductivity in cuprates and iron pnictides, Fermi liquid theory, quantum critical behavior, and frustrated magnetism. He is a fellow of the APS.

Compensated electron and hole pockets in an underdoped high- $T_{c}$ superconductor

Suchitra E. Sebastian, N. Harrison, P. A. Goddard, M. M. Altarawneh, C. H. Mielke, Ruixing Liang, D. A. Bonn, W. N. Hardy, O. K. Andersen, and G. G. Lonzarich

Phys. Rev. B 81, 214524 (2010)

Published June 28, 2010

Read PDF