Backward lasing yields a perfect absorber

Stefano Longhi

Viewpoint

Backward lasing yields a perfect absorber

Department of Physics, Polytechnic Institute of Milan, Milan, Italy

July 26, 2010• Physics 3, 61

Just as a laser can emit coherent light from an amplifying medium, an absorbing medium can perfectly capture incoming radiation under the right conditions.

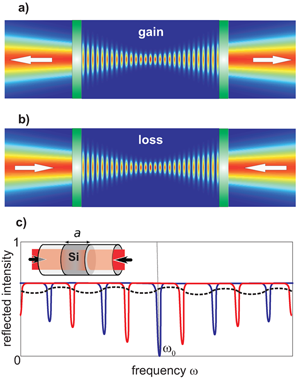
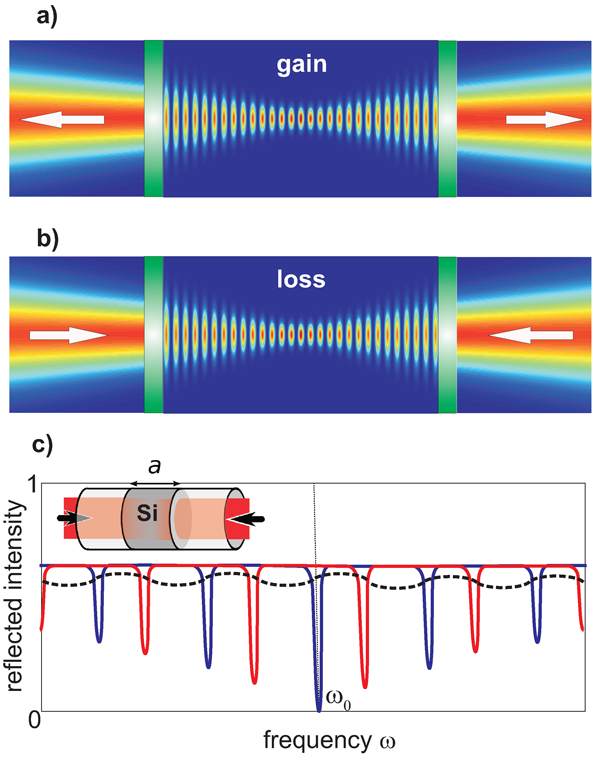
Figure caption — **Figure 1:** (a) Schematic of a laser oscillator: a gain medium with complex refractive index $n = n^{'} + i n^{''}$ , embedded in an optical cavity, emits outgoing coherent waves with defined phase and spatial pattern at frequency $ω_{0}$ when the amount of amplification $n^{''}$ reaches a threshold value. (b) Schematic of the time-reversed laser oscillator that realizes a coherent perfect absorber: when the gain medium is replaced by an absorbing medium with complex refractive index $n^{*} = n^{'} - i n^{''}$ , incoming waves with definite phase and spatial pattern [the time-reversed waves of the lasing mode in (a)] are fully absorbed in the medium. (c) Typical behavior of total intensity reflection coefficient versus frequency in a simple two-port photonic device, comprising a slab of lossy material (like $Si$ ) of thickness $a$ embedded in a fiber or waveguide (inset), excited at the two input sides. The red and blue lines show the spectral reflection curves for coherent input waves with controlled phase difference $Δ θ$ ( $Δ θ = 0$ , blue curve; $Δ θ = π$ , red curve). The dashed black line depicts the spectral reflection curve for incoherent input waves. The peaks in the coherent reflection curves correspond to the odd- and even-symmetric modes sustained by the slab structure.

It is well known that an amplifying medium embedded in an optical cavity, i.e., a laser oscillator, can emit coherent electromagnetic radiation when the gain coefficient of photons in the medium reaches a threshold value that balances the light leakage out of the cavity [1]. The emitted radiation escapes from the cavity in the form of outgoing monochromatic waves, usually along preferred spatial directions [see Fig. 1(a)]. The frequency $ω_{0}$ and spatial pattern of the emitted waves are those of the electromagnetic mode sustained by the leaky cavity, which experiences the largest amplification in the gain medium.

A less familiar process is the time-reversed counterpart of a laser: by replacing the gain with absorption, the same optical system supports a purely incoming radiation pattern with complete absorption and zero reflection [see Fig. 1(b)]. Such an optical system, referred to as a coherent perfect absorber (CPA), has been theoretically proposed in an article appearing in Physical Review Letters by Yidong Chong, Li Ge, Hui Cao, and Douglas Stone at Yale University in the US [2]. In this device, even small single-pass absorption can lead to perfect overall absorption, and optical media that normally do not absorb radiation well at certain frequencies, can be made to do so.

When light hits a material, three things can happen: light can be reflected, as by a mirror; it can be transmitted, as with window glass; or it can be absorbed and turned, for example, into heat. The time-reverse of the lasing process ensures that a coherent light shining on a dissipative medium at a specific wavelength and with appropriate spatial pattern is neither reflected nor transmitted, rather it is fully absorbed. This kind of coherent perfect absorption extends and explains in an elegant way previous known methods of absorption enhancement in integrated optical devices [3,4]. As compared to other perfect optical absorbers, such as those based on engineered metamaterials [5], the CPA principle proposed by Chong et al. [2] works for any kind of absorbing medium, is not based on resonant material absorption, and does not require material nanostructuring.

Perfect absorption of photons by a dissipative optical medium as proposed by the authors is reminiscent of the problem of perfect absorbing potentials for matter waves investigated in computational quantum physics, for example, in reactive scattering calculations or other molecular collision studies [6–9]. Perfect absorption of optical and matter waves share a similar mathematical description, involving the search for poles and zeros of the underlying scattering matrix, which relates the incoming and outgoing electromagnetic wave modes. Just as in a laser at the onset of oscillation, coherent perfect absorption provides a clear physical signature of certain spectral singularities that arise in the underlying non-Hermitian Hamiltonian [10,11]. However, the picture of coherent perfect absorption as time-reversed laser oscillation provides a simple and elegant explanation of the underlying physics that does not require any advanced knowledge of scattering or spectral theory.

In a dielectric optical cavity filled by a gain medium, the spatial profile of the lasing mode is found as an eigenfunction of the Helmholtz equation for the complex electric field amplitude $E$ , which in the simplest one-dimensional spatial case reads

where $n (x) = n^{'} + i n^{''}$ is the complex refractive index of the dielectric medium, and $c_{0}$ is the speed of light in a vacuum. The electric field inside and outside the cavity is simply given by $E (x, t) = E (x) exp (i ω t) + E^{*} (x) exp (- i ω t)$ . The imaginary part $n^{''}$ of the refractive index accounts for light amplification $(n^{''} > 0)$ or absorption $(n^{''} < 0)$ in the medium. For a laser, the outgoing radiation pattern $E (x)$ satisfies Eq. (1) for a real frequency $ω_{0}$ when the (positive) imaginary part $n^{''}$ of the refractive index reaches a threshold value. Outside the resonator, the field has the form of outgoing waves with appropriate amplitudes $A_{\pm}$ and phases $θ_{\pm}$ , i.e., $E (x) = A_{\pm} exp (\pm i k x + i θ_{\pm})$ .

If we take the complex conjugate of Eq. (1), i.e., if we consider the time-reversed process of lasing at threshold, it follows that $E^{*}$ again satisfies the Helmholtz equation but in a medium with a refractive index $n^{*} (x) = n^{'} - i n^{''}$ , i.e., in a lossy medium with the amount of loss exactly equal to the amount of gain in the original lasing medium. Since complex conjugation of the field pattern $E^{*}$ replaces outgoing waves with incoming waves, the dielectric lossy medium inside the cavity fully absorbs the incoming radiation pattern at frequency $ω_{0}$ , and thus acts as a perfect absorber. In other words, the combination of cavity effects and material absorption enables the incident radiation to be fully turned into heat, or re-radiated, without being reflected. Just like laser radiation, however, perfect absorption only occurs within narrow frequency bands, requires spatial mode matching and phase control of the incoming waves, and is observed for special values of the dissipation. Nevertheless, Chong et al. [2] have shown that such conditions can be realized using, for example, an indirect band-gap semiconductor (like silicon) in a waveguide configuration.

The simplest CPA they propose is a two-port device consisting of a silicon slab of thickness $a$ and (imaginary) refractive index $n = n^{'} - i n^{''}$ , embedded in a waveguide or fiber with (real) refractive index $n_{0}$ . The waveguide is excited from the two input sides by two counterpropagating coherent fields with the same intensity, same frequency $ω$ , and phase difference $Δ θ = θ_{+} - θ_{-}$ [see the inset of Fig. 1(c)]. The spectral behavior of the light intensity reflected from the two ports of the device, normalized to the total intensity of incident waves, is shown in Fig. 1(c) for coherent input excitation with $Δ θ = 0$ (blue curve), $Δ θ = π$ (red curve), and for incoherent beam excitation (dashed black curve). For coherent excitation, resonant peaks, leading to strong absorption in the material, are clearly visible, which correspond to the various resonant modes supported by the silicon slab with either odd or even spatial symmetry. The exact condition of time reversal of lasing, and thus perfect absorption, is attained at a special frequency $ω_{0}$ solely, which is the wavelength of the lasing mode that one would observe when the loss is replaced by gain. Conversely, for incoherent light excitation the resonant structure of the absorption greatly disappears. For the silicon slab design considered by the authors [2], the spectral peaks of perfect (or enhanced) absorption occur at around $940$ - $nm$ wavelength. It is remarkable that CPA enables not only a resonant enhancement of absorption, but also a reduction of absorption, as compared to incoherent excitation, for appropriate choice of the phase difference $Δ θ$ [2] [see Fig. 1(c)].

The main limitations of CPA are the narrow-band operation and the need for coherent (phase and spatially controlled) excitation fields. Such severe conditions make CPA unlikely in applications where absorption of broadband and incoherent light is needed (such as in solar photovoltaic or stealth applications). However, owing to the strong phase-dependence of the amount of absorbed radiation in the medium, CPA can be ingeniously exploited to build a compact absorptive multichannel interferometer, as discussed by Chong et al. [2]. Unlike an ordinary interferometer, a CPA-based interferometer does not shift the input beams between possible output channels, but causes them to be absorbed within the material. CPA-based interferometers could thus have potential applications in the realization of transducers, modulators, or optical switches, for example, in on-chip integrated optical circuits based on $Si$ waveguide/resonator technology.

References

A. E. Siegman, Lasers (University Science Books, Mill Valley, CA, 1986)[Amazon][WorldCat]
Y. D. Chong, L. Ge, H. Cao, and A. D. Stone, Phys. Rev. Lett. 105, 053901 (2010)
M. Cai, O. Painter, and K. J. Vahala, Phys. Rev. Lett. 85, 74 (2000)
J. R. Tischler, M. S. Bradley, and V. Bulovic, Opt. Lett. 31, 2045 (2006)
N. I. Landy, S. Sajuyigbe, J. J. Mock, D. R. Smith, and W. J. Padilla, Phys. Rev. Lett. 100, 207402 (2008)
J. P. Palao, J. G. Muga, and R. Sala, Phys. Rev. Lett. 80, 5469 (1998)
J. G. Muga, J. P. Palao, B. Navarro, and I. L. Egusquiza, Phys. Rep. 395, 357 (2004)
O. Shemer, D. Brisker, and N. Moiseyev, Phys. Rev. A 71, 032716 (2004)
X. Antoine, A. Arnold, C. Besse, M. Ehrhardt, and A. Schädle, Comm. Comp. Phys. 4, 729 (2008)
A. Mostafazadeh, Phys. Rev. Lett. 102, 220402 (2009)
S. Longhi, Phys. Rev. Lett. 105, 013903 (2010)

About the Author

Stefano Longhi received his Ph.D. in physics in 1996, and since 2003 he has been Associate Professor of Physics of Matter at the Polytechnic Institute of Milan, Italy. His research interests range from laser physics to nonlinear optics, quantum optics, and photonics. Professor Longhi is a Fellow of the Institute of Physics. In 2003 he was awarded with the Fresnel Prize of the European Physical Society for his outstanding contributions in the fields of optics and photonics.