In pursuit of a nameless metal
The metals that we understand are governed by Landau’s Fermi-liquid theory. This theory is built on the remarkably successful guess that the low-energy degrees of freedom of a metal are like electrons, in that they are long-lived fermionic particles carrying electric charge, but they are “dressed” to account for the interactions between them. This guess successfully describes fermionic helium ( He- 3), and most metals studied before the 1980s. However, Fermi-liquid theory fails rather spectacularly for many materials, which are so poorly understood that they are called “non-Fermi liquids” (NFL) or “strange metals,” for lack of a better name. (The most notorious examples of strange metals arise from the high-temperature cuprate superconductors.)
The feature that can make metals interesting—numerous low-energy degrees of freedom and hence the possibility of novel dynamics near the ground state—is exactly what makes them difficult to understand. Unlike insulators, which have no zero-energy modes, or a semimetal like graphene that only has gapless modes at points in momentum space, a metal has a whole surface (the Fermi surface) in momentum space of low-energy excitations. Complicating matters still more, the straightforward application of numerical methods is thwarted by the “fermion sign problem,” the fact that simulating a system of fermions requires keeping track of the delicate cancellation of many positive and negative contributions.
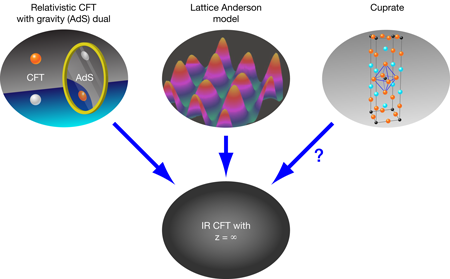
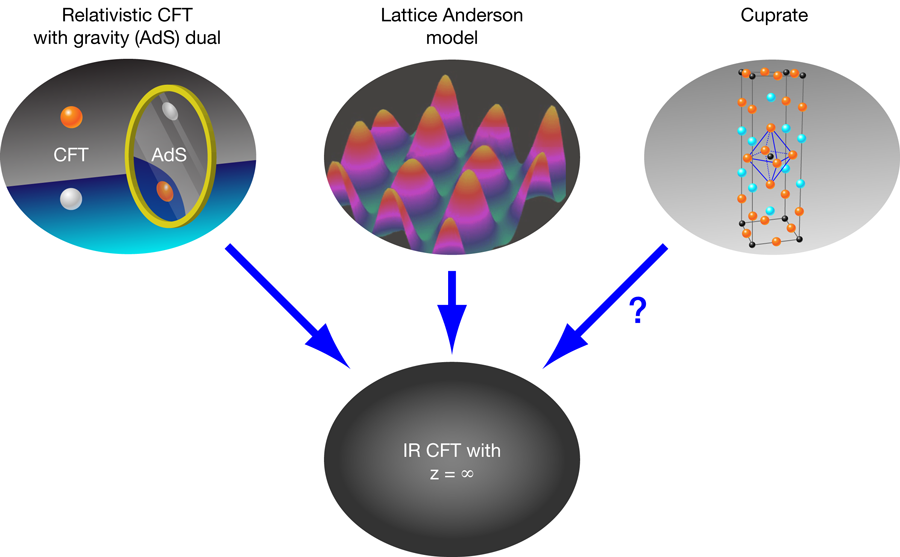
In a paper appearing in Physical Review Letters, Subir Sachdev [1] of Harvard University in the US draws together two diverse approaches to a theoretical description of strange metals that, while still imperfect, capture the essential behavior of these states of matter. In both approaches, the system under study is different microscopically from real materials that exhibit non-Fermi-liquid behavior: One is based on a model that is familiar in condensed matter physics, while the other uses what is called the AdS/CFT correspondence, which is a by now well-established duality between a theory of gravity and a gauge theory. The value of Sachdev’s work is therefore to identify effective descriptions of non-Fermi-liquid states. In another sense, his paper also represents an ongoing effort to adapt the tools of string theory (the AdS/CFT correspondence) to the study of many-body systems in condensed matter.
There are two key properties of a strange metal. First, the single-particle lifetime is short. This quantity can be measured by angle-resolved photoemission spectroscopy (ARPES). When photoemission data is available, it shows a sharp Fermi surface (in momentum space), but the degrees of freedom there are not long-lived quasiparticles. Second, compared to a Fermi liquid, a strange metal has a large electrical resistivity ρ at low temperatures T. For example, whereas a clean Fermi liquid has a resistivity that scales as T2, the resistivity of the strange metal phase of the cuprates is linear in temperature. Many other materials exhibit similar scaling, ρ∼Tα with α≳ [2]. Although electron interactions with lattice vibrations can explain the linear- scaling at high temperature, this explanation doesn’t hold at low temperatures.
There are theoretical models of Fermi surfaces without long-lived quasiparticles. One possibility that has received some attention is to assume the existence of a critical bosonic mode whose fluctuations literally kill the quasiparticles (for a recent discussion, see, for example, Ref. [3]). However, the resulting states in this model are not strange metals in the sense of transport, since the process by which the quasiparticle decays does not change the electric current very much. The interaction with the boson is not efficient at dissipating the momentum of the charge carriers [4] and as a result, the electrical resistivity predicted by this model continues to be weaker at low temperatures than in a strange metal and goes like with some .
The purpose of Sachdev’s work is to draw parallels between two apparently different models of non-Fermi liquids that do give such efficient current dissipation (Fig. 1). One is a “lattice Anderson model” and builds on work by Sachdev with Jinwu Ye (now at Pennsylvania State University) [5]. This model assumes that conduction electrons interact with another band of electrons, regarded as atomic orbitals, that have a random probability of being able to hop to a neighboring site. In a certain limit (of large electron spin and large number of dimensions), a self-consistent low-energy effective description of the -orbital spin degrees of freedom gives a model of non-Fermi-liquid behavior that captures the above properties.
The other approach, based on the AdS/CFT correspondence, has a much less obvious connection with any real material. Some relativistic gauge theories with a gauge group of large rank can be solved in terms of a classical theory of gravity living in one extra dimension [6]. (This difference in dimensions is the origin of the word “holographic” that describes the duality between these two theories.) The description in terms of gravity is valid when the gauge theory in question is strongly coupled and therefore hard to study otherwise. Including only the minimal ingredients needed to ask about the spectrum of a fermionic operator (as measured in a photoemission experiment), one can use the gravity description to show that the gauge theories have non-Fermi-liquid fixed points [7–11], with the resistivity determined by the single-particle lifetime [12], as in phenomenological models of the cuprates.
Both of these approaches to non-Fermi-liquid physics share a key ingredient: they contain degrees of freedom with the right energy spectrum to kill the quasiparticles and make a contribution to the electrical resistivity that is large at low temperature. Specifically, these degrees of freedom live not just at zero momentum, but are also easily excited at nonzero momentum. In fact, in the language of renormalization group theory, both descriptions “flow” toward an infrared (IR) fixed point quantum field theory with scaling symmetry in time but not in space: , with dynamical exponent . (Specifically, at the IR fixed-point, the single-fermion spectrum and the resistivity are controlled by the dimension of a certain operator.) Sachdev argues that the -orbital electrons in the lattice model are described at low energies by the IR fixed point he studied previously with Ye, where “local criticality” arises out of making the large-dimension approximation. Such scaling is ubiquitous in the condensed matter theory literature; it is an ingredient of the popular “dynamical mean field theory” (DMFT) technique. The approach from extra dimensions can also be described as a Fermi surface interacting with locally critical degrees of freedom [10–12]. The infinite- behavior of this IR fixed point is an output of the holographic duality under certain assumptions, which we discuss next.
One consequence of the infinite dynamical exponent in both approaches is a macroscopic ground-state degeneracy—a violation of the third law of thermodynamics. In practice, the third law is enforced because any small perturbation will lift the ground-state degeneracy. As a result, both approaches should be considered models of physics at energy scales intermediate between the lattice scale and the temperature below which one reaches the true ground state. The Fermi-liquid theory itself is such a theory (though the Fermi-liquid theory is remarkable in that BCS superconductivity sets in only at temperatures exponentially small compared to the Fermi energy). Of course, we know one example of a strange metal phase that develops an instability as the system is cooled: high-temperature superconductors. It is possible to describe superconductivity from the holographic point of view (for a review, see Ref. [13]) and the resulting spectrum of fermions has been studied, starting with [14–16]. The analogous study is likely being done for the Sachdev-Ye phase as I write this article.
One of the most interesting outcomes of the unification advocated by Sachdev is that in both approaches, one finds a “landscape” of values of the critical exponent that controls the single-particle lifetime. In the Sachdev and Ye approach, one value of the exponent is selected by the simplest self-consistency condition, but other values are possible [17]; in the holographic approach, there is no such indication of a preferred value. This usage of the word “landscape,” a term that comes from the study of glasses, is now something of a bugbear in string theory. It is emblematic of the oft-lamented difficulties in using string theory to make predictions for particle physics because of the huge multiplicity of string vacua. There is a consolation though. Many of these ground states are holographically dual to quantum field theories that can describe a class of many-body systems at low energy—the landscape of string vacua mirrors the landscape of possible many-body phenomena.
At present, we are far from having a precise match between a specific model that describes the behavior of strange metals and a real material. Rather, this is a broad opportunity to make contact between string theory and experiment. But for the study of strange metals, the existing models of the intermediate-scale fixed point suggest that many values of the fermion critical exponent should be possible. Revisiting the data in various non-Fermi-liquid materials with this in mind may be rewarding.
Sachdev’s paper describes a dramatic manifestation of universality—the same class of fixed points is reached from completely different microscopic models, each of which differs from the materials that are observed to exhibit the physics of interest (Fig. 1). This is encouraging for those of us hoping to apply string theory to condensed matter physics—this new perspective on the thus-far mysterious results from holographic duality brings them closer to models of electrons in solids.
Acknowledgments
I am grateful to Steve Shenker and Subir Sachdev for discussions about the landscape of exponents, to Brian Swingle for comments on the draft, and to Tom Faulkner, Nabil Iqbal, Hong Liu, and David Vegh for collaboration on related matters. This work was supported in part by funds provided by the U.S. Department of Energy (D.O.E.) under cooperative research agreement DE-FG0205ER41360, and in part by the Alfred P. Sloan foundation.
Correction (14 October 2010): Paragraph 8, sentence 5, “large- approximation” changed to “large-dimension approximation” to avoid potential confusion with the that refers to the type of orbitals in the lattice model.
References
- S. Sachdev, Phys. Rev. Lett. 105, 151602 (2010)
- G. R. Stewart, Rev. Mod. Phys. 73, 797 (2001); 78, 743 (2006)
- A. Chubukov, Physics 3, 70 (2010)
- Patrick A. Lee and Naoto Nagaosa, Phys. Rev. B 46, 5621 (1992)
- S. Sachdev and J. Ye, Phys. Rev. Lett. 70, 3339 (1993)
- J. M. Maldacena, Adv. Theor. Math. Phys. 2, 231 (1998); E. Witten, Adv. Theor. Math. Phys. 2, 505 (1998); S. S. Gubser, I. R. Klebanov, and A. M. Polyakov, Phys. Lett. B 428, 105 (1998)
- S. S. Lee, arXiv:0809.3402 (hep-th)
- H. Liu, J. McGreevy, and D. Vegh, arXiv:0903.2477 (hep-th)
- M. Cubrovic, J. Zaanen, and K. Schalm, arXiv:0904.1993 (hep-th); Science 325, 439 (2009)
- T. Faulkner, H. Liu, J. McGreevy, and D. Vegh, arXiv:0907.2694 (hep-th)
- T. Faulkner and J. Polchinski, arXiv:1001.5049 (hep-th)
- T. Faulkner, N. Iqbal, H. Liu, J. McGreevy, and D. Vegh, Science 329, 1043 (2010)
- G. T. Horowitz, arXiv:1002.1722 (hep-th)
- J. W. Chen, Y. J. Kao, and W. Y. Wen, arXiv:0911.2821 (hep-th)
- T. Faulkner, G. T. Horowitz, J. McGreevy, M. M. Roberts, D. Vegh, arXiv:0911.3402 (hep-th)
- S. S. Gubser, F. D. Rocha, and P. Talavera, arXiv:0911.3632 (hep-th)
- A. Georges, R. Siddharthan, and S. Florens, Phys. Rev. Lett. 87 277203 (2001)