A quantitative look into microorganism hydrodynamics

David Saintillan

Viewpoint

A quantitative look into microorganism hydrodynamics

Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA

October 11, 2010• Physics 3, 84

Direct measurements show that the fluid flow around swimming microorganisms is more complex than previously thought, with important implications for how they interact and behave.

Figure caption — **Figure 1:** Flow field around a swimming *Volvox carteri*. The spherical *Volvox*, located at the center of the image, is swimming towards the top. Streamlines appear as red curves, and the color map corresponds to the fluid velocity magnitude. As demonstrated by Drescher and co-workers, this flow can be accurately described as the superposition of a Stokeslet and source doublet, with a small stresslet contribution [1].

Microorganisms, such as bacteria, microphytes (tiny plants such as microscopic algae), and protists (a diverse group of single cell organisms), are present in every part of the biosphere: giant plankton blooms in the oceans, protozoa in our lakes and ponds, beneficial or pathogenic bacteria in our bodies are but a few examples that we are all familiar with. The ability of microorganisms to move through fluid environments is critical to biological and ecological functions as diverse as reproduction, pathogenic infection, mixing and ${CO}_{2}$ capture in the oceans, among many others. Our understanding of their motility mechanisms, dynamics, and interactions remains limited, however, in part owing to our lack of quantitative information about the flows they generate on the microscale. In articles published in Physical Review Letters, two different research groups present measurements of the flow fields driven by swimming microorganisms. In the first study, Knut Drescher and co-workers at the University of Cambridge, UK, describe the first detailed quantitative measurements of the time-averaged flows around two different types of model swimming microalgae: Volvox carteri and Chlamydomonas reinhardtii [1]. In the second article, Jeffrey Guasto and co-workers at Haverford College, US, also measure the flow field driven by Chlamydomonas reinhardtii, but focus on its oscillatory nature using time-resolved measurements [2]. Both studies clearly demonstrate that these flow fields are more complex than was previously believed, opening the door for new and more accurate models for the hydrodynamics of microorganismal colonies.

Because of their tiny sizes (on the order of $1$ to $200 μ m$ ), microorganisms evolve in the realm of low Reynolds numbers, in which viscous effects are predominant and inertia is negligible [3]. In this regime, the flow disturbance driven by the motion of a body or particle (such as a swimming microorganism) depends linearly upon the stresses exerted by the body on the fluid, and typically decays very slowly with the distance $r$ from the body center [4]. These flow disturbances can be described as linear superpositions of fundamental solutions of the Stokes equations, which decay as inverse powers of $r$ . The first such solution, coined the “Stokeslet,” arises from the net force on the fluid, and has a velocity field that decays like $1 / r$ in three dimensions. At the next level, the “stresslet” flow, which is induced by the first force moment exerted by the particle on the fluid, decays more rapidly like $1 / r^{2}$ . Higher-order solutions include the “source doublet” and “force quadrupole,” with velocities decaying as $1 / r^{3}$ . Linear combinations of these basic solutions can yield various flows with complex and qualitatively different near-field and far-field behaviors. These behaviors in turn have a strong impact on the nature of interactions among microorganisms and between microorganisms and surfaces, with significant implications for their collective dynamics.

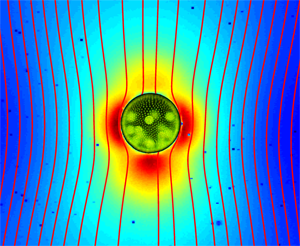
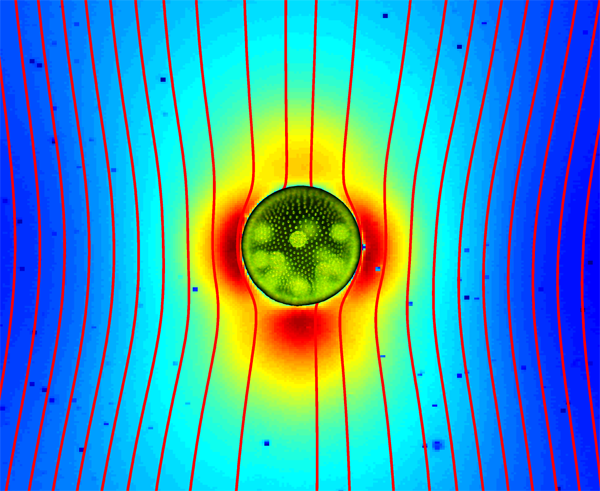
Up until recently, it was firmly believed that the flow field around a swimming microorganism could be faithfully described as a stresslet flow, driven by the balance between the thrust and drag forces on the organism, which results in an effective force dipole. Drescher et al. demonstrate that the situation is far from being that simple [1]. Using an experimental technique known as particle image velocimetry, which consists of tracking the motion of small passive tracer beads suspended in a fluid, they were able to reconstruct the flow fields around individual swimming microphytes of two different types, and to analyze them in terms of the basic flow solutions described above. The two species they studied are Volvox carteri, a relatively large multicellular spherical alga that swims as a result of the flagellar beating of the thousands of cells embedded in its surface, and Chlamydomonas reinhardtii, a small unicellular green alga that propels by beating two flagella in a breaststroke-like fashion. Based on their measurements, they found that the flow around Volvox (illustrated in Fig. 1) is very well described by the superposition of a Stokeslet and a source doublet, with only a minor stresslet contribution. The presence of a nonzero Stokeslet is due to the density of Volvox, which is slightly higher than that of water, and suggests that the flow field far away from Volvox is in fact qualitatively similar to that of a particle sedimenting under gravity. On the other hand, the time-averaged flow generated by Chlamydomonas is best captured in the far field by a positive stresslet; in the near field where the strongest velocities occur, it is highly complex but can be modeled fairly accurately by three off-centered Stokeslets.

In the second article, Guasto et al. [2] also use particle image velocimetry to measure the flow field around Chlamydomonas. Their study, however, differs from that of Drescher et al. in two ways: the swimming microorganisms are now confined in a stabilized thin liquid film, and a high-speed digital camera is used for imaging, allowing them to measure time-resolved flow fields over one period of motion, corresponding to one breaststroke by the microalga. The time-averaged velocity fields they obtain are consistent with those obtained by Drescher et al., albeit characterized by a slower decay rate as $1 / r$ in the far-field owing to the two-dimensional film geometry. However, they also demonstrate that fluctuations with respect to the time-averaged flow over the course of one stroke are very strong and even result in a reversal of the flow over a significant portion of the period of motion. This surprising observation suggests that modeling the hydrodynamics of microorganisms such as Chlamydomonas in terms of a time-averaged flow is overly simplistic, as it may miss important dynamics arising from the inherently oscillatory nature of the flow.

A direct implication of these results lies in the nature of interactions among swimming microorganisms and with surfaces or boundaries. As several microorganisms swim in the vicinity of one another, the flow disturbances they create around them modify the motion of their neighbors in a nontrivial way. In large colonies, these fluid-mediated interactions, known as hydrodynamic interactions, can result in large-scale flows and collective dynamics [5], whose characteristics depend critically on the nature of the single-swimmer flow fields [6,7]. According to the results of Drescher et al., we can expect interactions between swimming Volvox to resemble interactions between sedimenting particles, and to be qualitatively different from those between Chlamydomonas. In each case, far-field and near-field interactions are also very likely to differ. Finally, the study by Guasto et al. also suggests that the nature of these interactions may change over the course of one breaststroke by Chlamydomonas, and will also depend on whether the organisms that are interacting are swimming in or out of phase. These predictions will surely spur new improvements to the existing models for hydrodynamic interactions between microorganisms, which have so far been based on simplifying assumptions for lack of detailed information about the flow fields generated by the swimmers.

In addition to causing particle interactions, the flow fields driven by microorganisms also have the effect of mixing the fluid around them. This mixing may be critical for the survival and growth of microorganismal colonies, as it provides easier access to nutrients and oxygen [5,8]. It may also play a part in quorum sensing, which is the ability of some types of bacteria to release and detect chemical cues in the fluid around them as a means of regulating the expression of certain genes [9]. Mixing is also likely to be of importance in the oceans [10], where plankton plays a key role in the carbon cycle and is at the base of the marine food web. As demonstrated by recent experiments [11], models [12], and computer simulations [13,14], the effectiveness of microorganisms at mixing the fluid around them again hinges on the nature of the disturbance flows they generate, which advect fluid elements in a random fashion. The far-field behavior of these disturbances (and specifically their stresslet contribution) can in some cases set up large-scale flows that contribute to mixing via chaotic advection [13], whereas near-field fluctuations result in small local fluid displacements akin to a random walk [11,12,14].

The studies by the Cambridge and Haverford groups, by providing the first detailed quantitative picture of the flow fields driven by freely swimming microalgae, demonstrate three important points: (i) the flows around swimming microorganisms can be quite complex, especially in the near field where the largest velocities arise; (ii) two distinct species are likely to drive qualitatively different disturbance flows, including in the far field, where it is often assumed that the flow fields can be universally described in terms of a stresslet; (iii) the representation of these flows in terms of time-averaged velocity fields is simplistic, as time fluctuations can be of the same order as the mean. The implications of these findings in terms of hydrodynamic interactions and mixing are far-reaching and will only be fully understood once the details of these flows are incorporated into mathematical models or computer simulations. We can also hope that this study will spur additional experimental work in this area, using other species such as bacteria, whose disturbance flows are also expected to differ significantly and have yet to be measured with the same level of detail.

Correction (14 October 2010): Paragraph 4, sentence 3, ”…characterized by a faster decay rate” changed to ”…characterized by a slower decay rate.”

References

K. Drescher, R. E. Goldstein, N. Michel, M. Polin, and I. Tuval, Phys. Rev. Lett. 105, 168101 (2010)
J. S. Guasto, K. A. Johnson, and J. P. Gollub, Phys. Rev. Lett. 105, 168102 (2010)
E. Lauga and T. R. Powers, Rep. Prog. Phys. 72, 096601 (2009)
J. Happel and H. Brenner, Low Reynolds number hydrodynamics with special applications to particulate media (Kluwer, Boston, 1983)[Amazon][WorldCat]
I. Tuval, L. Cisneros, C. Dombrowski, C. W. Wolgemuth, J. O. Kessler, and R. E. Golstein, Proc. Natl. Acad. Sci. USA 102, 2277 (2005)
D. Saintillan and M. J. Shelley, Phys. Rev. Lett. 99, 058102 (2007)
D. Saintillan and M. J. Shelley, Phys. Rev. Lett. 100, 178103 (2008)
A. Sokolov, R. E. Goldstein, F. I. Feldchtein, and I. S. Aranson, Phys. Rev. E 80, 031903 (2009)
R. J. Redfield, Trends Microbiol. 10, 365 (2002)
F. Peters, C. Marrase, H. Havskum, F. Rassoulzadegan, J. Dolan, M. Alcaraz, and J. M. Gasol, J. Plankton Res. 24, 321 (2002)
K. C. Leptos, J. S. Guasto, J. P. Gollub, A. I. Pesci, and R. E. Goldstein, Phys. Rev. Lett. 103, 198103 (2009)
J. L. Thiffeault and S. Childress, Phys. Lett. A 374, 3487 (2010)
D. Saintillan and M. J. Shelley, Phys. Fluids 20, 123304 (2008)
T. Ishikawa, J. T. Locsei, and T. J. Pedley, Phys. Rev. E 82, 021408 (2010)

About the Author

David Saintillan is an Assistant Professor of Mechanical Science and Engineering at the University of Illinois at Urbana-Champaign. He received a B.S. in Engineering from Ecole Polytechnique, France, in 2001, and an M.S. and a Ph.D. in Mechanical Engineering from Stanford University in 2003 and 2006. He then worked as a Junior Research Scientist at the Courant Institute of Mathematical Sciences of New York University before joining the University of Illinois in 2008. He was the recipient of the Andreas Acrivos Dissertation Award in Fluid Dynamics of the American Physical Society in 2007. His research focuses on complex fluids, biophysical fluid dynamics, and electrokinetics.