Snakes and ladders
Turbulence, with its unruly and apparently unpredictable swirls, is a notoriously difficult problem to describe mathematically. But the laminar (or streamlined) flow from which turbulence arises can be described by very simple solutions of the Navier-Stokes equations. And, experimentally, it is known that turbulent patches exist within, and later perturb, surrounding laminar flow. This suggests that understanding the coexistence of laminar and turbulent regions is important for clarifying how flows become turbulent.
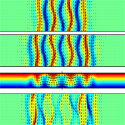
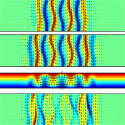
An essential step, argue Tobias Schneider at Harvard University, John Gibson at the Georgia Institute of Technology, and John Burke at Boston University, all in the US, is to find solutions of the Navier-Stokes equations that support complex, three-dimensional structure in localized patches, which are surrounded by smooth, laminar flow. Writing in Physical Review Letters, Schneider, Gibson, and Burke find such localized solutions in a flow driven by two counter-propagating plates (plane Couette flow). For a given Reynolds number, Schneider et al. find multiple localized solutions, with different sizes but similar interior structure. These solutions can be connected to each other smoothly through variations in the Reynolds number, giving rise to “snaking” behavior in the solution bifurcation diagram that is strikingly similar to that observed in simpler partial-differential equation systems from pattern formation theory.
The results are important because they suggest connections between turbulence and pattern-formation theory, and they show that the Navier-Stokes equations have global solutions with localized structure, which may prove an important tool with which to describe transitional turbulence. – Jessica Thomas