Twisting and turning towards new multiferroics

Gavin Lawes

Viewpoint

Twisting and turning towards new multiferroics

Department of Physics and Astronomy, Wayne State University, Detroit, Michigan 48201, USA

March 7, 2011• Physics 4, 18

Controlling the rotation and tilt of oxygen octahedra in perovskite structures provides a new route towards room-temperature multiferroics.

Figure caption — **Figure 1:** (a) ${Ca}_{3} {Mn}_{2} O_{7}$ structure in its distorted ferroelectric state. $Mn$ ions (green) are surrounded by oxygen octahedra (green with red $O$ ions) with $Ca$ ions (blue) interspersed. (b) Octahedral rotation ( $R$ ) in ${Ca}_{3} {Mn}_{2} O_{7}$ , showing the oxygen (blue) and manganese (red) sites. The undistorted structure is shown in grayscale. (c) Octahedral tilt ( $T$ ) of the same. The combination of the tilt and rotation combine to produce ferroelectric order.

Magnetoelectric multiferroics are materials that exhibit coupled magnetic and ferroelectric order, and are studied from a desire for electric field control of magnetization [1]. Realizing this promise in new systems provides an interesting challenge for experimentalists and theoreticians alike in the search for candidate materials [2]. The quest is to identify mechanisms that can simultaneously break spatial inversion symmetry to allow ferroelectric order and break time reversal symmetry to allow magnetic order, while also providing a coupling between these two distinct types of order. The search for such materials has provided a number of promising results, including the simultaneous development of strongly coupled magnetic and ferroelectric order in ${TbMnO}_{3}$ [3], albeit at low temperatures, and the observation of a large ferroelectric polarization in epitaxial ${BiFeO}_{3}$ [4] films, the as-yet sole example of a room-temperature, single-phase multiferroic. However, despite the concerted research efforts, the discovery of multiferroics exhibiting controllable reversal of the magnetization with an electric field at ambient temperatures has remained elusive.

In a paper appearing in Physical Review Letters [5], Nicole Benedek and Craig Fennie from Cornell University, US, offer a fresh approach for introducing magnetoelectrically coupled multiferroic order in layered perovskite mineral through multiple lattice distortions. Building on recent work by Bousquet and co-workers, demonstrating that ferroelectricity is produced by local rotational modes in a ${SrTiO}_{3} / {PbTiO}_{3}$ superlattice [6], Benedek and Fennie propose that magnetoelectric coupling, weak ferromagnetism, and ferroelectricity can develop from the combination of two lattice rotations, neither of which produces ferroelectric order individually (see Fig. 1). While previous studies on multiferroics have shown that two distinct magnetic structures can combine to break spatial inversion to promote ferroelectric order [7], Benedek and Fennie demonstrate that separate lattice distortions can not only produce ferroelectricity, but also modify the magnetic order and promote a magnetoelectric coupling. This offers a new deterministic approach to introducing multiferroic order, with the possibility of identifying systems having these properties well above room temperature.

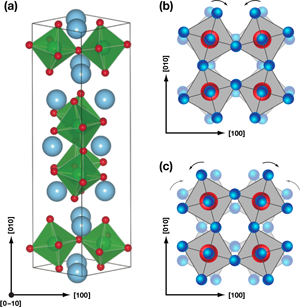
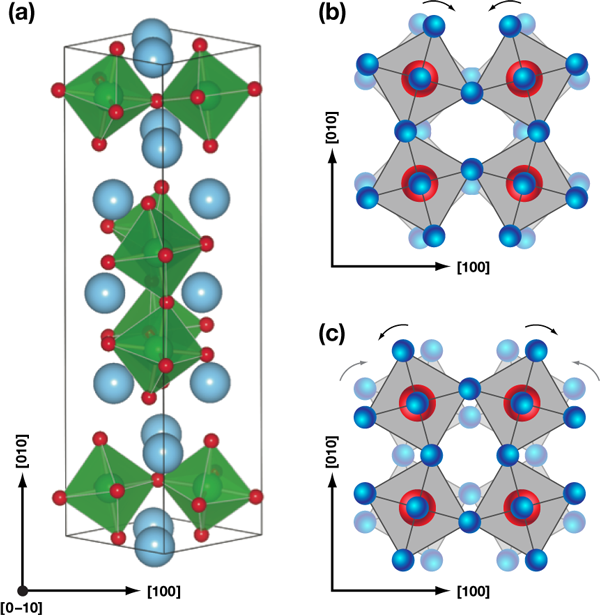
Benedek and Fennie use the layered perovskite ${Ca}_{3} {Mn}_{2} O_{7}$ as a model system to illustrate this mechanism for producing ferroelectric order coupled to magnetic properties. The crystal structure of ${Ca}_{3} {Mn}_{2} O_{7}$ consists of layers of corner-sharing ${MnO}_{6}$ octahedra, with two layers of ${CaMnO}_{3}$ for every sheet of $CaO$ [see Fig. 1(a)]. Their analysis shows that the paraelectric state of this mineral can transform into a ferroelectric one through the combination of a rotation distortion ( $R$ ) [Fig. 1(b)] and a tilt distortion ( $T$ ) [Fig. 1(c)] of the oxygen octahedra. The distortions can occur at the same temperatures or different temperatures, and while neither of these distortions breaks spatial inversion independently, the combination $R T$ can produce a ferroelectric polarization. The fact that the polarization is proportional to the product of these two distortions immediately suggests that the ferroelectric polarization will flip direction if either $R$ or $T$ , though not both, is reversed. Their symmetry-based proposal—that ferroelectricity arises from a combination of two separate distortions—is supported by their first-principles calculations, which find a large ferroelectric polarization $P \approx 5 μ {C cm}^{- 2}$ and confirms the reversal in the polarization direction on changing the sign of either $R$ or $T$ .

Benedek and Fennie’s model shows that the same lattice distortions that coalesce to promote ferroelectricity can also modify the magnetic structure, and produce the linear magnetoelectric coupling required for electric-field control of the magnetization. The small net magnetization associated with this antiferromagnetic structure emerges because of the tilting of the oxygen octahedral represented by $T$ . First-principles calculations by Benedek and Fennie show that reversing the octahedral tilt $T$ flips the magnetic moment, while varying the octahedral rotation $R$ does not change the direction of the magnetization. In principle, this allows a mechanism for independently controlling the polarization and magnetization by varying $R$ or $T$ .

Beyond ferroelectricity and (weak) ferromagnetism, the last requirement for developing useful multiferroics is the presence of a linear magnetoelectric effect. Fortuitously, this coupling also emerges from the octahedral rotations and tilts. The rotation distortion $R$ on top of the high-temperature crystal produces a magnetic ground state with a symmetry that allows for a linear magnetoelectric coupling. With this final piece of the puzzle, this case study on ${Ca}_{3} {Mn}_{2} O_{7}$ illustrates how rotations and tilts can provide a net magnetic moment (arising from $T$ ), a linear magnetoelectric coupling (from $R$ ), and a ferroelectric polarization (from the product $R T$ ). However, in order to be useful for most device applications, the net magnetization in a multiferroic should be controllable using an applied electric field. Estimates by Benedek and Fennie suggest that on reversing an applied electric field, the ferroelectric polarization switches direction by changing the rotation $R$ . Modifying this distortion does not affect the net magnetic moment, confounding the expectation of electric field control of the magnetization in ${Ca}_{3} {Mn}_{2} O_{7}$ .

Fortunately, there may be a solution to this conundrum. Reflecting the interest in using epitaxial strain as a tool to modify the properties of multiferroic materials [8], Benedek and Fennie also explore the effects of strain on this system. As mentioned previously, the lowest energy pathway to reverse the polarization in bulk ${Ca}_{3} {Mn}_{2} O_{7}$ is to flip the direction of the octahedral rotation $R$ , which does not affect the direction of the magnetization. Happily, adding a $1.5 %$ compressive strain to the system shifts the lowest energy pathway to reversing the direction of the octahedral tilt $T$ , which does change the direction of the net magnetization. This means that switching the direction of the polarization using an external electric field in strained ${Ca}_{3} {Mn}_{2} O_{7}$ thin films should reverse the direction of the magnetization. More provocatively, this electric control of the magnetization should also to arise in other related materials, even in bulk geometries.

The recognition that coincident ferroelectric and magnetic order with an associated magnetoelectric coupling can arise from specific combinations of lattice distortions represents a significant advance in the study and design of multiferroic materials. Although the low temperature ( $115 K$ ) for the development of magnetic order in ${Ca}_{3} {Mn}_{2} O_{7}$ means that this system is unlikely to ever be incorporated in devices, the mechanism proposed by Benedek and Fennie is broadly applicable to a wide class of materials. The structural distortions producing this ferroelectricity and magnetoelectric coupling can generically manifest near or above room temperature, so there appears to be no fundamental limitation on the temperature range over which this mechanism could produce multiferroic order. This is not just another material in the multiferroic bestiary—as the authors succinctly point out, this approach to designing useful room-temperature multiferroics shifts the burden from discovering materials with suitable magnetoelectric coupling to the more tractable problem of identifying room-temperature antiferromagnets. The increasingly nuanced understanding of ferroelectrics and magnetoelectrics by design, reflected in this Letter by Benedek and Fennie, presages a sharp expansion in the role of room-temperature multiferroics, making it likely that these materials will finally meet their promise of ushering in a new era of spin-charge coupled electronics.

References

D. Khomskii, Physics 2, 20 (2009)
N. A. Hill, J. Phys. Chem. B 104, 6694 (2000)
T. Kimura et al., Nature 425, 55 (2003)
J. Wang et al., Science 299, 1719 (2003)
N. A. Benedek and C. J. Fennie, Phys. Rev. Lett. 106, 107204 (2011)
E. Bousquet et al., Nature 452, 732 (2008)
A. B. Harris, Phys. Rev. B 76, 054447 (2007)
J. H. Lee et al., Nature 466, 954 (2010)

About the Author

Gavin Lawes is an associate professor of physics at Wayne State University. He received his Ph.D. from Cornell University in 2001, which was followed by a postdoctoral position at Los Alamos National Laboratory. He joined the faculty of the Department of Physics and Astronomy at Wayne State University as an assistant professor in 2004. His research interests are focused on novel magnetic materials, including magnetoelectrics and multiferroics, magnetic nanoparticles, and magnetic semiconductors.