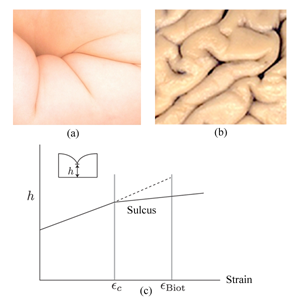
Folding furrows

Christian D. Santangelo

Viewpoint

Folding furrows

Christian D. Santangelo

Department of Physics, University of Massachusetts, Amherst, MA 01003, USA

March 7, 2011• Physics 4, 19

Folds on the surface of soft materials are shown to be a consequence of a nonlinear instability.

Figure caption — **Figure 1:** Localized folds, called sulci, induced on soft materials due to compressive stresses are ubiquitous in nature: (a) the arm of an infant, (b) a primate brain. (c) Schematic illustration of a bifurcation diagram showing the scaled height $h$ of a sulcus plotted against the applied strain. A sulcus nucleates at a critical strain $ϵ_{c}$ due to a spontaneous breaking of scale symmetry.

Even as we probe physics on ever-smaller scales, materials that can be held and manipulated with our hands often still resist our understanding. Elastic materials, in particular, still confound because of the nonlinear relationship between strain and the displacement of the material needed to maintain the rotational invariance of the elastic energy. The effects of these nonlinearities are often more pronounced at free surfaces, where strain can be alleviated by a large rotation of the surface. When a slab of an elastic material such as rubber is compressed, it develops a sulcus—a sharp furrow in its surface that plunges into the material. First reported for photographic gelatin films over one hundred years ago, they are not just a laboratory curiosity. Sulci create large strains that can lead to material failure. They are also a common motif in the morphogenesis of many organs, most famously in the characteristic folds on the surface of the human brain or, say, the arm of an infant [see Fig. 1(a) and (b)]. Though a mechanism for the formation of a sulcus was proposed almost fifty years ago [1], a complete understanding has remained elusive [2–6]. Now, in a paper appearing in Physical Review Letters, Evan Hohlfeld from Harvard University and Lawrence Berkeley National Laboratory and L. Mahadevan from Harvard University have proposed that the formation of a sulcus is controlled by a new type of instability dominated by nonlinearities in the elastic energy [7]. Their case is bolstered both by detailed numerics and by experiments. Moreover, they suggest that similar nonlinear instabilities may be lurking behind the formation of many other singular structures found in materials.

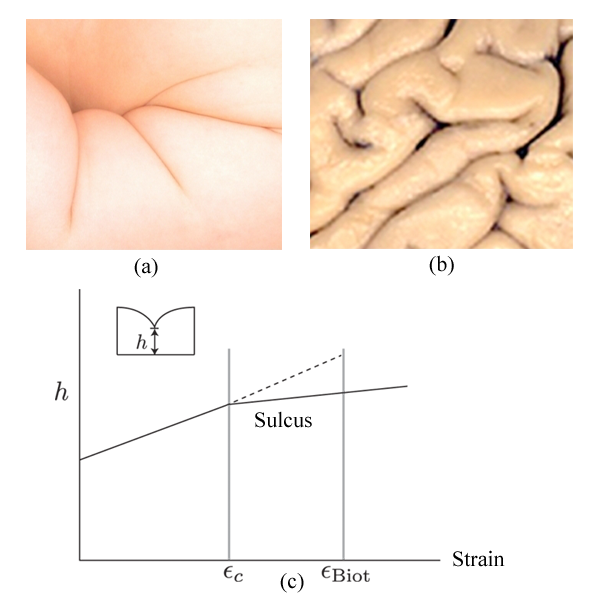
In the calculation of Biot, a free surface of a compressed elastic material becomes unstable at a critical strain of $45.6 %$ [1]. Indeed, experiments show that a compressed slab forms sharp furrows above some critical strain. Rather than develop as an instability, however, the sulci in experiments nucleate and grow laterally as fully formed furrows. Moreover, this often occurs at a lower strain of $35 %$ [2–4], noticeably smaller than the location of the Biot instability. The observed behavior suggests that an energy barrier exists between a material with a smooth surface and one with a sharp furrow, leading to a first-order transition to a sulcus of finite depth.

Hohlfeld and Mahadevan have performed both numerical simulations and experiments to better understand how sulci develop [7,8]. In their simulations, they consider an incompressible elastic material with a free surface. Since the formation of a sulcus involves length scales shorter than the scale of the elastic elements in their simulation, they introduce a cutoff length scale by using a thin crust on the surface that penalizes curvature. They then use a numerical limiting process to decrease the stiffness of the crust to zero. As the crust vanishes, they find a new critical point occurring at a lower critical strain, $35.4 %$ , very close to what is observed in experiments [see Fig. 1(c)]. A sulcus then unfolds continuously upon unloading. It is this unusual behavior of the nonlinear critical point that distinguishes the formation of a sulcus from a first-order transition.

Why does Biot’s calculation fail? At its most basic level, the failure is in the approximation of linear elasticity. This occurs because the elastic energy, in the absence of a crust, is scale-free and, as the numerical solutions demonstrate, sulci of different depths are self-similar. Consequently, the stress balance in the material remains unaltered, no matter the sulcus height. Nonlinearities, important for large deformations, must also be important even for the most shallow sulci. The introduction of a crust or some other surface energy, by introducing a length scale, results in the energy barrier between smooth surfaces and sulci often seen in experiments [6].

The calculation of Hohlfeld and Mahadevan also explains the inconsistent experimental results. At the nonlinear critical point, where sulci of any depth are degenerate, the formation of a sulcus requires the spontaneous breaking of scale symmetry. Subsequently, the ultimate scale of a sulcus is very sensitive to either the finite depth of a slab or the scale-setting imperfections of any real material. Hohlfeld and Mahadevan also performed experiments to bolster their calculations, finding good agreement between their numerical calculations with essentially no fitting parameters. A later numerical calculation of creasing in an inextensible gel also finds a critical point for forming a sulcus at a strain of $35 %$ [9]. Rather than imposing a length scale through a crust, the symmetry is explicitly broken in the numerics by choosing boundary conditions that force a sulcus to form. The nonlinear instability occurs when the energy of forming a sulcus becomes degenerate with that of a smooth surface.

This result can be viewed in the context of another nonlinear instability. An elastic film floating on a fluid also exhibits a linear wrinkling instability with a characteristic wavelength upon compression. Above a critical strain, however, the wrinkled state gives way to a large fold [10]. Diamant and Witten have argued that, here too, nonlinear corrections can preempt the linear wrinkling instability in infinite systems [11].

The analysis of the formation of a sulcus suggests that similar nonlinear instabilities may occur in any scale-free system with free boundaries that form singularitylike structures. The formation of cavities, bubbles, and cracks not only share these features, but their nucleation is notoriously sensitive to experimental details. The work of Hohlfeld and Mahadevan may provide a framework to organize and perhaps, ultimately, control the formation of singular structures in materials.

References

M. A. Biot, Appl. Sci. Res. A 12, 168 (1963)
T. Tanaka, S.-T. Sun, Y. Hirokawa, S. Katayama, J. Kucera, Y. Hirose, and T. Amiya, Nature 325, 796 (1987)
E. Southern A. G. Thomas, J. Polym. Sci. A, 3,641 (1965)
A. N. Gent and I. S. Cho, Rubber Chem. Technol. 72, 253 (1999)
V. Trujillo, J. Kim, and R. C. Hayward, Soft Matter 4, 564 (2008)
J. Yoon, J. Kim, and R. C. Hayward, Soft Matter 6, 5807 (2010)
E. Hohlfeld and L. Mahadevan, Phys. Rev. Lett. 106, 105702 (2011)
E. Hohlfeld, Ph.D. thesis, Harvard University, 2008 (unpublished)
W. Hong, X. Zhao, and Z. Suo, Appl. Phys. Lett. 95, 111901 (2009)
L. Pocivavsek et al., Science 320, 912 (2008)
H. Diamant and T. C. Witten, arXiv:1009.2487 (2010)

About the Author

Christian Santangelo received his Ph.D. in 2004 from the University of California at Santa Barbara. He did his postdoctoral work at the University of Pennsylvania from 2004 to 2007. In 2006, he was the recipient of the Glenn Brown Prize, awarded by the International Liquid Crystal Society. In 2007, he joined the faculty of the University of Massachusetts Amherst as an assistant professor. His research focuses on the geometry and nonlinear elasticity of elastic sheets and liquid crystals. In 2008, he was awarded a CAREER grant to study the wrinkling of swelled elastic sheets.